can we time travel with quantum physics

Can we time travel? A theoretical physicist provides some answers

Emeritus professor, Physics, Carleton University

Disclosure statement

Peter Watson received funding from NSERC. He is affiliated with Carleton University and a member of the Canadian Association of Physicists.

Carleton University provides funding as a member of The Conversation CA.

Carleton University provides funding as a member of The Conversation CA-FR.

View all partners

• Bahasa Indonesia

Time travel makes regular appearances in popular culture, with innumerable time travel storylines in movies, television and literature. But it is a surprisingly old idea: one can argue that the Greek tragedy Oedipus Rex , written by Sophocles over 2,500 years ago, is the first time travel story .

But is time travel in fact possible? Given the popularity of the concept, this is a legitimate question. As a theoretical physicist, I find that there are several possible answers to this question, not all of which are contradictory.

The simplest answer is that time travel cannot be possible because if it was, we would already be doing it. One can argue that it is forbidden by the laws of physics, like the second law of thermodynamics or relativity . There are also technical challenges: it might be possible but would involve vast amounts of energy.

There is also the matter of time-travel paradoxes; we can — hypothetically — resolve these if free will is an illusion, if many worlds exist or if the past can only be witnessed but not experienced. Perhaps time travel is impossible simply because time must flow in a linear manner and we have no control over it, or perhaps time is an illusion and time travel is irrelevant.

Laws of physics

Since Albert Einstein’s theory of relativity — which describes the nature of time, space and gravity — is our most profound theory of time, we would like to think that time travel is forbidden by relativity. Unfortunately, one of his colleagues from the Institute for Advanced Study, Kurt Gödel, invented a universe in which time travel was not just possible, but the past and future were inextricably tangled.

We can actually design time machines , but most of these (in principle) successful proposals require negative energy , or negative mass, which does not seem to exist in our universe. If you drop a tennis ball of negative mass, it will fall upwards. This argument is rather unsatisfactory, since it explains why we cannot time travel in practice only by involving another idea — that of negative energy or mass — that we do not really understand.

Mathematical physicist Frank Tipler conceptualized a time machine that does not involve negative mass, but requires more energy than exists in the universe .

Time travel also violates the second law of thermodynamics , which states that entropy or randomness must always increase. Time can only move in one direction — in other words, you cannot unscramble an egg. More specifically, by travelling into the past we are going from now (a high entropy state) into the past, which must have lower entropy.

This argument originated with the English cosmologist Arthur Eddington , and is at best incomplete. Perhaps it stops you travelling into the past, but it says nothing about time travel into the future. In practice, it is just as hard for me to travel to next Thursday as it is to travel to last Thursday.

Resolving paradoxes

There is no doubt that if we could time travel freely, we run into the paradoxes. The best known is the “ grandfather paradox ”: one could hypothetically use a time machine to travel to the past and murder their grandfather before their father’s conception, thereby eliminating the possibility of their own birth. Logically, you cannot both exist and not exist.

Read more: Time travel could be possible, but only with parallel timelines

Kurt Vonnegut’s anti-war novel Slaughterhouse-Five , published in 1969, describes how to evade the grandfather paradox. If free will simply does not exist, it is not possible to kill one’s grandfather in the past, since he was not killed in the past. The novel’s protagonist, Billy Pilgrim, can only travel to other points on his world line (the timeline he exists in), but not to any other point in space-time, so he could not even contemplate killing his grandfather.

The universe in Slaughterhouse-Five is consistent with everything we know. The second law of thermodynamics works perfectly well within it and there is no conflict with relativity. But it is inconsistent with some things we believe in, like free will — you can observe the past, like watching a movie, but you cannot interfere with the actions of people in it.

Could we allow for actual modifications of the past, so that we could go back and murder our grandfather — or Hitler ? There are several multiverse theories that suppose that there are many timelines for different universes. This is also an old idea: in Charles Dickens’ A Christmas Carol , Ebeneezer Scrooge experiences two alternative timelines, one of which leads to a shameful death and the other to happiness.

Time is a river

Roman emperor Marcus Aurelius wrote that:

“ Time is like a river made up of the events which happen , and a violent stream; for as soon as a thing has been seen, it is carried away, and another comes in its place, and this will be carried away too.”

We can imagine that time does flow past every point in the universe, like a river around a rock. But it is difficult to make the idea precise. A flow is a rate of change — the flow of a river is the amount of water that passes a specific length in a given time. Hence if time is a flow, it is at the rate of one second per second, which is not a very useful insight.

Theoretical physicist Stephen Hawking suggested that a “ chronology protection conjecture ” must exist, an as-yet-unknown physical principle that forbids time travel. Hawking’s concept originates from the idea that we cannot know what goes on inside a black hole, because we cannot get information out of it. But this argument is redundant: we cannot time travel because we cannot time travel!

Researchers are investigating a more fundamental theory, where time and space “emerge” from something else. This is referred to as quantum gravity , but unfortunately it does not exist yet.

So is time travel possible? Probably not, but we don’t know for sure!

• Time travel
• Stephen Hawking
• Albert Einstein
• Listen to this article
• Time travel paradox
• Arthur Eddington

Head of School, School of Arts & Social Sciences, Monash University Malaysia

Chief Operating Officer (COO)

Clinical Teaching Fellow

Data Manager

Director, Social Policy

Help | Advanced Search

General Relativity and Quantum Cosmology

Title: emergent time and time travel in quantum physics.

Abstract: Entertaining the possibility of time travel will invariably challenge dearly held concepts of fundamental physics. It becomes relatively easy to construct multiple logical contradictions using differing starting points from various well-established fields of physics. Sometimes, the interpretation is that only a full theory of quantum gravity will be able to settle these logical contradictions. Even then, it remains unclear if the multitude of problems could be overcome. Yet as definitive as this seems to the notion of time travel in physics, such a recourse to quantum gravity comes with its own, long-standing challenge to most of these counter-arguments to time travel: These arguments rely on time, while quantum gravity is (in)famously stuck with and dealing with the problem of time. One attempt to answer this problem within the canonical framework resulted in the Page-Wootters formalism, and its recent gauge-theoretic re-interpretation - as an emergent notion of time. Herein, we will begin a programme to study toy models implementing the Hamiltonian constraint in quantum theory, with an aim towards understanding what an emergent notion of time can tell us about the (im)possibility of time travel.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Time Travel and Modern Physics

Time travel has been a staple of science fiction. With the advent of general relativity it has been entertained by serious physicists. But, especially in the philosophy literature, there have been arguments that time travel is inherently paradoxical. The most famous paradox is the grandfather paradox: you travel back in time and kill your grandfather, thereby preventing your own existence. To avoid inconsistency some circumstance will have to occur which makes you fail in this attempt to kill your grandfather. Doesn’t this require some implausible constraint on otherwise unrelated circumstances? We examine such worries in the context of modern physics.

1. Paradoxes Lost?

2. topology and constraints, 3. the general possibility of time travel in general relativity, 4. two toy models, 5. slightly more realistic models of time travel, 6. the possibility of time travel redux, 7. even if there are constraints, so what, 8. computational models, 9. quantum mechanics to the rescue, 10. conclusions, other internet resources, related entries.

• Supplement: Remarks and Limitations on the Toy Models

Modern physics strips away many aspects of the manifest image of time. Time as it appears in the equations of classical mechanics has no need for a distinguished present moment, for example. Relativity theory leads to even sharper contrasts. It replaces absolute simultaneity, according to which it is possible to unambiguously determine the time order of distant events, with relative simultaneity: extending an “instant of time” throughout space is not unique, but depends on the state of motion of an observer. More dramatically, in general relativity the mathematical properties of time (or better, of spacetime)—its topology and geometry—depend upon how matter is arranged rather than being fixed once and for all. So physics can be, and indeed has to be, formulated without treating time as a universal, fixed background structure. Since general relativity represents gravity through spacetime geometry, the allowed geometries must be as varied as the ways in which matter can be arranged. Alongside geometrical models used to describe the solar system, black holes, and much else, the scope of variation extends to include some exotic structures unlike anything astrophysicists have observed. In particular, there are spacetime geometries with curves that loop back on themselves: closed timelike curves (CTCs), which describe the possible trajectory of an observer who returns exactly back to their earlier state—without any funny business, such as going faster than the speed of light. These geometries satisfy the relevant physical laws, the equations of general relativity, and in that sense time travel is physically possible.

Yet circular time generates paradoxes, familiar from science fiction stories featuring time travel: [ 1 ]

• Consistency: Kurt plans to murder his own grandfather Adolph, by traveling along a CTC to an appropriate moment in the past. He is an able marksman, and waits until he has a clear shot at grandpa. Normally he would not miss. Yet if he succeeds, there is no way that he will then exist to plan and carry out the mission. Kurt pulls the trigger: what can happen?
• Underdetermination: Suppose that Kurt first travels back in order to give his earlier self a copy of How to Build a Time Machine. This is the same book that allows him to build a time machine, which he then carries with him on his journey to the past. Who wrote the book?
• Easy Knowledge: A fan of classical music enhances their computer with a circuit that exploits a CTC. This machine efficiently solves problems at a higher level of computational complexity than conventional computers, leading (among other things) to finding the smallest circuits that can generate Bach’s oeuvre—and to compose new pieces in the same style. Such easy knowledge is at odds with our understanding of our epistemic predicament. (This third paradox has not drawn as much attention.)

The first two paradoxes were once routinely taken to show that solutions with CTCs should be rejected—with charges varying from violating logic, to being “physically unreasonable”, to undermining the notion of free will. Closer analysis of the paradoxes has largely reversed this consensus. Physicists have discovered many solutions with CTCs and have explored their properties in pursuing foundational questions, such as whether physics is compatible with the idea of objective temporal passage (starting with Gödel 1949). Philosophers have also used time travel scenarios to probe questions about, among other things, causation, modality, free will, and identity (see, e.g., Earman 1972 and Lewis’s seminal 1976 paper).

We begin below with Consistency , turning to the other paradoxes in later sections. A standard, stone-walling response is to insist that the past cannot be changed, as a matter of logic, even by a time traveler (e.g., Gödel 1949, Clarke 1977, Horwich 1987). Adolph cannot both die and survive, as a matter of logic, so any scheme to alter the past must fail. In many of the best time travel fictions, the actions of a time traveler are constrained in novel and unexpected ways. Attempts to change the past fail, and they fail, often tragically, in just such a way that they set the stage for the time traveler’s self-defeating journey. The first question is whether there is an analog of the consistent story when it comes to physics in the presence of CTCs. As we will see, there is a remarkable general argument establishing the existence of consistent solutions. Yet a second question persists: why can’t time-traveling Kurt kill his own grandfather? Doesn’t the necessity of failures to change the past put unusual and unexpected constraints on time travelers, or objects that move along CTCs? The same argument shows that there are in fact no constraints imposed by the existence of CTCs, in some cases. After discussing this line of argument, we will turn to the palatability and further implications of such constraints if they are required, and then turn to the implications of quantum mechanics.

Wheeler and Feynman (1949) were the first to claim that the fact that nature is continuous could be used to argue that causal influences from later events to earlier events, as are made possible by time travel, will not lead to paradox without the need for any constraints. Maudlin (1990) showed how to make their argument precise and more general, and argued that nonetheless it was not completely general.

Imagine the following set-up. We start off having a camera with a black and white film ready to take a picture of whatever comes out of the time machine. An object, in fact a developed film, comes out of the time machine. We photograph it, and develop the film. The developed film is subsequently put in the time machine, and set to come out of the time machine at the time the picture is taken. This surely will create a paradox: the developed film will have the opposite distribution of black, white, and shades of gray, from the object that comes out of the time machine. For developed black and white films (i.e., negatives) have the opposite shades of gray from the objects they are pictures of. But since the object that comes out of the time machine is the developed film itself it we surely have a paradox.

However, it does not take much thought to realize that there is no paradox here. What will happen is that a uniformly gray picture will emerge, which produces a developed film that has exactly the same uniform shade of gray. No matter what the sensitivity of the film is, as long as the dependence of the brightness of the developed film depends in a continuous manner on the brightness of the object being photographed, there will be a shade of gray that, when photographed, will produce exactly the same shade of gray on the developed film. This is the essence of Wheeler and Feynman’s idea. Let us first be a bit more precise and then a bit more general.

For simplicity let us suppose that the film is always a uniform shade of gray (i.e., at any time the shade of gray does not vary by location on the film). The possible shades of gray of the film can then be represented by the (real) numbers from 0, representing pure black, to 1, representing pure white.

Let us now distinguish various stages in the chronological order of the life of the film. In stage \(S_1\) the film is young; it has just been placed in the camera and is ready to be exposed. It is then exposed to the object that comes out of the time machine. (That object in fact is a later stage of the film itself). By the time we come to stage \(S_2\) of the life of the film, it has been developed and is about to enter the time machine. Stage \(S_3\) occurs just after it exits the time machine and just before it is photographed. Stage \(S_4\) occurs after it has been photographed and before it starts fading away. Let us assume that the film starts out in stage \(S_1\) in some uniform shade of gray, and that the only significant change in the shade of gray of the film occurs between stages \(S_1\) and \(S_2\). During that period it acquires a shade of gray that depends on the shade of gray of the object that was photographed. In other words, the shade of gray that the film acquires at stage \(S_2\) depends on the shade of gray it has at stage \(S_3\). The influence of the shade of gray of the film at stage \(S_3\), on the shade of gray of the film at stage \(S_2\), can be represented as a mapping, or function, from the real numbers between 0 and 1 (inclusive), to the real numbers between 0 and 1 (inclusive). Let us suppose that the process of photography is such that if one imagines varying the shade of gray of an object in a smooth, continuous manner then the shade of gray of the developed picture of that object will also vary in a smooth, continuous manner. This implies that the function in question will be a continuous function. Now any continuous function from the real numbers between 0 and 1 (inclusive) to the real numbers between 0 and 1 (inclusive) must map at least one number to itself. One can quickly convince oneself of this by graphing such functions. For one will quickly see that any continuous function \(f\) from \([0,1]\) to \([0,1]\) must intersect the line \(x=y\) somewhere, and thus there must be at least one point \(x\) such that \(f(x)=x\). Such points are called fixed points of the function. Now let us think about what such a fixed point represents. It represents a shade of gray such that, when photographed, it will produce a developed film with exactly that same shade of gray. The existence of such a fixed point implies a solution to the apparent paradox.

Let us now be more general and allow color photography. One can represent each possible color of an object (of uniform color) by the proportions of blue, green and red that make up that color. (This is why television screens can produce all possible colors.) Thus one can represent all possible colors of an object by three points on three orthogonal lines \(x, y\) and \(z\), that is to say, by a point in a three-dimensional cube. This cube is also known as the “Cartesian product” of the three line segments. Now, one can also show that any continuous map from such a cube to itself must have at least one fixed point. So color photography can not be used to create time travel paradoxes either!

Even more generally, consider some system \(P\) which, as in the above example, has the following life. It starts in some state \(S_1\), it interacts with an object that comes out of a time machine (which happens to be its older self), it travels back in time, it interacts with some object (which happens to be its younger self), and finally it grows old and dies. Let us assume that the set of possible states of \(P\) can be represented by a Cartesian product of \(n\) closed intervals of the reals, i.e., let us assume that the topology of the state-space of \(P\) is isomorphic to a finite Cartesian product of closed intervals of the reals. Let us further assume that the development of \(P\) in time, and the dependence of that development on the state of objects that it interacts with, is continuous. Then, by a well-known fixed point theorem in topology (see, e.g., Hocking & Young 1961: 273), no matter what the nature of the interaction is, and no matter what the initial state of the object is, there will be at least one state \(S_3\) of the older system (as it emerges from the time travel machine) that will influence the initial state \(S_1\) of the younger system (when it encounters the older system) so that, as the younger system becomes older, it develops exactly into state \(S_3\). Thus without imposing any constraints on the initial state \(S_1\) of the system \(P\), we have shown that there will always be perfectly ordinary, non-paradoxical, solutions, in which everything that happens, happens according to the usual laws of development. Of course, there is looped causation, hence presumably also looped explanation, but what do you expect if there is looped time?

Unfortunately, for the fan of time travel, a little reflection suggests that there are systems for which the needed fixed point theorem does not hold. Imagine, for instance, that we have a dial that can only rotate in a plane. We are going to put the dial in the time machine. Indeed we have decided that if we see the later stage of the dial come out of the time machine set at angle \(x\), then we will set the dial to \(x+90\), and throw it into the time machine. Now it seems we have a paradox, since the mapping that consists of a rotation of all points in a circular state-space by 90 degrees does not have a fixed point. And why wouldn’t some state-spaces have the topology of a circle?

However, we have so far not used another continuity assumption which is also a reasonable assumption. So far we have only made the following demand: the state the dial is in at stage \(S_2\) must be a continuous function of the state of the dial at stage \(S_3\). But, the state of the dial at stage \(S_2\) is arrived at by taking the state of the dial at stage \(S_1\), and rotating it over some angle. It is not merely the case that the effect of the interaction, namely the state of the dial at stage \(S_2\), should be a continuous function of the cause, namely the state of the dial at stage \(S_3\). It is additionally the case that path taken to get there, the way the dial is rotated between stages \(S_1\) and \(S_2\) must be a continuous function of the state at stage \(S_3\). And, rather surprisingly, it turns out that this can not be done. Let us illustrate what the problem is before going to a more general demonstration that there must be a fixed point solution in the dial case.

Forget time travel for the moment. Suppose that you and I each have a watch with a single dial neither of which is running. My watch is set at 12. You are going to announce what your watch is set at. My task is going to be to adjust my watch to yours no matter what announcement you make. And my actions should have a continuous (single valued) dependence on the time that you announce. Surprisingly, this is not possible! For instance, suppose that if you announce “12”, then I achieve that setting on my watch by doing nothing. Now imagine slowly and continuously increasing the announced times, starting at 12. By continuity, I must achieve each of those settings by rotating my dial to the right. If at some point I switch and achieve the announced goal by a rotation of my dial to the left, I will have introduced a discontinuity in my actions, a discontinuity in the actions that I take as a function of the announced angle. So I will be forced, by continuity, to achieve every announcement by rotating the dial to the right. But, this rotation to the right will have to be abruptly discontinued as the announcements grow larger and I eventually approach 12 again, since I achieved 12 by not rotating the dial at all. So, there will be a discontinuity at 12 at the latest. In general, continuity of my actions as a function of announced times can not be maintained throughout if I am to be able to replicate all possible settings. Another way to see the problem is that one can similarly reason that, as one starts with 12, and imagines continuously making the announced times earlier, one will be forced, by continuity, to achieve the announced times by rotating the dial to the left. But the conclusions drawn from the assumption of continuous increases and the assumption of continuous decreases are inconsistent. So we have an inconsistency following from the assumption of continuity and the assumption that I always manage to set my watch to your watch. So, a dial developing according to a continuous dynamics from a given initial state, can not be set up so as to react to a second dial, with which it interacts, in such a way that it is guaranteed to always end up set at the same angle as the second dial. Similarly, it can not be set up so that it is guaranteed to always end up set at 90 degrees to the setting of the second dial. All of this has nothing to do with time travel. However, the impossibility of such set ups is what prevents us from enacting the rotation by 90 degrees that would create paradox in the time travel setting.

Let us now give the positive result that with such dials there will always be fixed point solutions, as long as the dynamics is continuous. Let us call the state of the dial before it interacts with its older self the initial state of the dial. And let us call the state of the dial after it emerges from the time machine the final state of the dial. There is also an intermediate state of the dial, after it interacts with its older self and before it is put into the time machine. We can represent the initial or intermediate states of the dial, before it goes into the time machine, as an angle \(x\) in the horizontal plane and the final state of the dial, after it comes out of the time machine, as an angle \(y\) in the vertical plane. All possible \(\langle x,y\rangle\) pairs can thus be visualized as a torus with each \(x\) value picking out a vertical circular cross-section and each \(y\) picking out a point on that cross-section. See figure 1 .

Figure 1 [An extended description of figure 1 is in the supplement.]

Suppose that the dial starts at angle \(i\) which picks out vertical circle \(I\) on the torus. The initial angle \(i\) that the dial is at before it encounters its older self, and the set of all possible final angles that the dial can have when it emerges from the time machine is represented by the circle \(I\) on the torus (see figure 1 ). Given any possible angle of the emerging dial, the dial initially at angle \(i\) will develop to some other angle. One can picture this development by rotating each point on \(I\) in the horizontal direction by the relevant amount. Since the rotation has to depend continuously on the angle of the emerging dial, circle \(I\) during this development will deform into some loop \(L\) on the torus. Loop \(L\) thus represents all possible intermediate angles \(x\) that the dial is at when it is thrown into the time machine, given that it started at angle \(i\) and then encountered a dial (its older self) which was at angle \(y\) when it emerged from the time machine. We therefore have consistency if \(x=y\) for some \(x\) and \(y\) on loop \(L\). Now, let loop \(C\) be the loop which consists of all the points on the torus for which \(x=y\). Ring \(I\) intersects \(C\) at point \(\langle i,i\rangle\). Obviously any continuous deformation of \(I\) must still intersect \(C\) somewhere. So \(L\) must intersect \(C\) somewhere, say at \(\langle j,j\rangle\). But that means that no matter how the development of the dial starting at \(I\) depends on the angle of the emerging dial, there will be some angle for the emerging dial such that the dial will develop exactly into that angle (by the time it enters the time machine) under the influence of that emerging dial. This is so no matter what angle one starts with, and no matter how the development depends on the angle of the emerging dial. Thus even for a circular state-space there are no constraints needed other than continuity.

Unfortunately there are state-spaces that escape even this argument. Consider for instance a pointer that can be set to all values between 0 and 1, where 0 and 1 are not possible values. That is, suppose that we have a state-space that is isomorphic to an open set of real numbers. Now suppose that we have a machine that sets the pointer to half the value that the pointer is set at when it emerges from the time machine.

Figure 2 [An extended description of figure 2 is in the supplement.]

Suppose the pointer starts at value \(I\). As before we can represent the combination of this initial position and all possible final positions by the line \(I\). Under the influence of the pointer coming out of the time machine the pointer value will develop to a value that equals half the value of the final value that it encountered. We can represent this development as the continuous deformation of line \(I\) into line \(L\), which is indicated by the arrows in figure 2 . This development is fully continuous. Points \(\langle x,y\rangle\) on line \(I\) represent the initial position \(x=I\) of the (young) pointer, and the position \(y\) of the older pointer as it emerges from the time machine. Points \(\langle x,y\rangle\) on line \(L\) represent the position \(x\) that the younger pointer should develop into, given that it encountered the older pointer emerging from the time machine set at position \(y\). Since the pointer is designed to develop to half the value of the pointer that it encounters, the line \(L\) corresponds to \(x=1/2 y\). We have consistency if there is some point such that it develops into that point, if it encounters that point. Thus, we have consistency if there is some point \(\langle x,y\rangle\) on line \(L\) such that \(x=y\). However, there is no such point: lines \(L\) and \(C\) do not intersect. Thus there is no consistent solution, despite the fact that the dynamics is fully continuous.

Of course if 0 were a possible value, \(L\) and \(C\) would intersect at 0. This is surprising and strange: adding one point to the set of possible values of a quantity here makes the difference between paradox and peace. One might be tempted to just add the extra point to the state-space in order to avoid problems. After all, one might say, surely no measurements could ever tell us whether the set of possible values includes that exact point or not. Unfortunately there can be good theoretical reasons for supposing that some quantity has a state-space that is open: the set of all possible speeds of massive objects in special relativity surely is an open set, since it includes all speeds up to, but not including, the speed of light. Quantities that have possible values that are not bounded also lead to counter examples to the presented fixed point argument. And it is not obvious to us why one should exclude such possibilities. So the argument that no constraints are needed is not fully general.

An interesting question of course is: exactly for which state-spaces must there be such fixed points? The arguments above depend on a well-known fixed point theorem (due to Schauder) that guarantees the existence of a fixed point for compact, convex state spaces. We do not know what subsequent extensions of this result imply regarding fixed points for a wider variety of systems, or whether there are other general results along these lines. (See Kutach 2003 for more on this issue.)

A further interesting question is whether this line of argument is sufficient to resolve Consistency (see also Dowe 2007). When they apply, these results establish the existence of a solution, such as the shade of uniform gray in the first example. But physicists routinely demand more than merely the existence of a solution, namely that solutions to the equations are stable—such that “small” changes of the initial state lead to “small” changes of the resulting trajectory. (Clarifying the two senses of “small” in this statement requires further work, specifying the relevant topology.) Stability in this sense underwrites the possibility of applying equations to real systems given our inability to fix initial states with indefinite precision. (See Fletcher 2020 for further discussion.) The fixed point theorems guarantee that for an initial state \(S_1\) there is a solution, but this solution may not be “close” to the solution for a nearby initial state, \(S'\). We are not aware of any proofs that the solutions guaranteed to exist by the fixed point theorems are also stable in this sense.

Time travel has recently been discussed quite extensively in the context of general relativity. General relativity places few constraints on the global structure of space and time. This flexibility leads to a possibility first described in print by Hermann Weyl:

Every world-point is the origin of the double-cone of the active future and the passive past [i.e., the two lobes of the light cone]. Whereas in the special theory of relativity these two portions are separated by an intervening region, it is certainly possible in the present case [i.e., general relativity] for the cone of the active future to overlap with that of the passive past; so that, in principle, it is possible to experience events now that will in part be an effect of my future resolves and actions. Moreover, it is not impossible for a world-line (in particular, that of my body), although it has a timelike direction at every point, to return to the neighborhood of a point which it has already once passed through. (Weyl 1918/1920 [1952: 274])

A time-like curve is simply a space-time trajectory such that the speed of light is never equaled or exceeded along this trajectory. Time-like curves represent possible trajectories of ordinary objects. In general relativity a curve that is everywhere timelike locally can nonetheless loop back on itself, forming a CTC. Weyl makes the point vividly in terms of the light cones: along such a curve, the future lobe of the light cone (the “active future”) intersects the past lobe of the light cone (the “passive past”). Traveling along such a curve one would never exceed the speed of light, and yet after a certain amount of (proper) time one would return to a point in space-time that one previously visited. Or, by staying close to such a CTC, one could come arbitrarily close to a point in space-time that one previously visited. General relativity, in a straightforward sense, allows time travel: there appear to be many space-times compatible with the fundamental equations of general relativity in which there are CTC’s. Space-time, for instance, could have a Minkowski metric everywhere, and yet have CTC’s everywhere by having the temporal dimension (topologically) rolled up as a circle. Or, one can have wormhole connections between different parts of space-time which allow one to enter “mouth \(A\)” of such a wormhole connection, travel through the wormhole, exit the wormhole at “mouth \(B\)” and re-enter “mouth \(A\)” again. CTCs can even arise when the spacetime is topologically \(\mathbb{R}^4\), due to the “tilting” of light cones produced by rotating matter (as in Gödel 1949’s spacetime).

General relativity thus appears to provide ample opportunity for time travel. Note that just because there are CTC’s in a space-time, this does not mean that one can get from any point in the space-time to any other point by following some future directed timelike curve—there may be insurmountable practical obstacles. In Gödel’s spacetime, it is the case that there are CTCs passing through every point in the spacetime. Yet these CTCs are not geodesics, so traversing them requires acceleration. Calculations of the minimal fuel required to travel along the appropriate curve should discourage any would-be time travelers (Malament 1984, 1985; Manchak 2011). But more generally CTCs may be confined to smaller regions; some parts of space-time can have CTC’s while other parts do not. Let us call the part of a space-time that has CTC’s the “time travel region” of that space-time, while calling the rest of that space-time the “normal region”. More precisely, the “time travel region” consists of all the space-time points \(p\) such that there exists a (non-zero length) timelike curve that starts at \(p\) and returns to \(p\). Now let us turn to examining space-times with CTC’s a bit more closely for potential problems.

In order to get a feeling for the sorts of implications that closed timelike curves can have, it may be useful to consider two simple models. In space-times with closed timelike curves the traditional initial value problem cannot be framed in the usual way. For it presupposes the existence of Cauchy surfaces, and if there are CTCs then no Cauchy surface exists. (A Cauchy surface is a spacelike surface such that every inextendable timelike curve crosses it exactly once. One normally specifies initial conditions by giving the conditions on such a surface.) Nonetheless, if the topological complexities of the manifold are appropriately localized, we can come quite close. Let us call an edgeless spacelike surface \(S\) a quasi-Cauchy surface if it divides the rest of the manifold into two parts such that

• every point in the manifold can be connected by a timelike curve to \(S\), and
• any timelike curve which connects a point in one region to a point in the other region intersects \(S\) exactly once.

It is obvious that a quasi-Cauchy surface must entirely inhabit the normal region of the space-time; if any point \(p\) of \(S\) is in the time travel region, then any timelike curve which intersects \(p\) can be extended to a timelike curve which intersects \(S\) near \(p\) again. In extreme cases of time travel, a model may have no normal region at all (e.g., Minkowski space-time rolled up like a cylinder in a time-like direction), in which case our usual notions of temporal precedence will not apply. But temporal anomalies like wormholes (and time machines) can be sufficiently localized to permit the existence of quasi-Cauchy surfaces.

Given a timelike orientation, a quasi-Cauchy surface unproblematically divides the manifold into its past (i.e., all points that can be reached by past-directed timelike curves from \(S)\) and its future (ditto mutatis mutandis ). If the whole past of \(S\) is in the normal region of the manifold, then \(S\) is a partial Cauchy surface : every inextendable timelike curve which exists to the past of \(S\) intersects \(S\) exactly once, but (if there is time travel in the future) not every inextendable timelike curve which exists to the future of \(S\) intersects \(S\). Now we can ask a particularly clear question: consider a manifold which contains a time travel region, but also has a partial Cauchy surface \(S\), such that all of the temporal funny business is to the future of \(S\). If all you could see were \(S\) and its past, you would not know that the space-time had any time travel at all. The question is: are there any constraints on the sort of data which can be put on \(S\) and continued to a global solution of the dynamics which are different from the constraints (if any) on the data which can be put on a Cauchy surface in a simply connected manifold and continued to a global solution? If there is time travel to our future, might we we able to tell this now, because of some implied oddity in the arrangement of present things?

It is not at all surprising that there might be constraints on the data which can be put on a locally space-like surface which passes through the time travel region: after all, we never think we can freely specify what happens on a space-like surface and on another such surface to its future, but in this case the surface at issue lies to its own future. But if there were particular constraints for data on a partial Cauchy surface then we would apparently need to have to rule out some sorts of otherwise acceptable states on \(S\) if there is to be time travel to the future of \(S\). We then might be able to establish that there will be no time travel in the future by simple inspection of the present state of the universe. As we will see, there is reason to suspect that such constraints on the partial Cauchy surface are non-generic. But we are getting ahead of ourselves: first let’s consider the effect of time travel on a very simple dynamics.

The simplest possible example is the Newtonian theory of perfectly elastic collisions among equally massive particles in one spatial dimension. The space-time is two-dimensional, so we can represent it initially as the Euclidean plane, and the dynamics is completely specified by two conditions. When particles are traveling freely, their world lines are straight lines in the space-time, and when two particles collide, they exchange momenta, so the collision looks like an “\(X\)” in space-time, with each particle changing its momentum at the impact. [ 2 ] The dynamics is purely local, in that one can check that a set of world-lines constitutes a model of the dynamics by checking that the dynamics is obeyed in every arbitrarily small region. It is also trivial to generate solutions from arbitrary initial data if there are no CTCs: given the initial positions and momenta of a set of particles, one simply draws a straight line from each particle in the appropriate direction and continues it indefinitely. Once all the lines are drawn, the worldline of each particle can be traced from collision to collision. The boundary value problem for this dynamics is obviously well-posed: any set of data at an instant yields a unique global solution, constructed by the method sketched above.

What happens if we change the topology of the space-time by hand to produce CTCs? The simplest way to do this is depicted in figure 3 : we cut and paste the space-time so it is no longer simply connected by identifying the line \(L-\) with the line \(L+\). Particles “going in” to \(L+\) from below “emerge” from \(L-\) , and particles “going in” to \(L-\) from below “emerge” from \(L+\).

Figure 3: Inserting CTCs by Cut and Paste. [An extended description of figure 3 is in the supplement.]

How is the boundary-value problem changed by this alteration in the space-time? Before the cut and paste, we can put arbitrary data on the simultaneity slice \(S\) and continue it to a unique solution. After the change in topology, \(S\) is no longer a Cauchy surface, since a CTC will never intersect it, but it is a partial Cauchy surface. So we can ask two questions. First, can arbitrary data on \(S\) always be continued to a global solution? Second, is that solution unique? If the answer to the first question is \(no\), then we have a backward-temporal constraint: the existence of the region with CTCs places constraints on what can happen on \(S\) even though that region lies completely to the future of \(S\). If the answer to the second question is \(no\), then we have an odd sort of indeterminism, analogous to the unwritten book: the complete physical state on \(S\) does not determine the physical state in the future, even though the local dynamics is perfectly deterministic and even though there is no other past edge to the space-time region in \(S\)’s future (i.e., there is nowhere else for boundary values to come from which could influence the state of the region).

In this case the answer to the first question is yes and to the second is no : there are no constraints on the data which can be put on \(S\), but those data are always consistent with an infinitude of different global solutions. The easy way to see that there always is a solution is to construct the minimal solution in the following way. Start drawing straight lines from \(S\) as required by the initial data. If a line hits \(L-\) from the bottom, just continue it coming out of the top of \(L+\) in the appropriate place, and if a line hits \(L+\) from the bottom, continue it emerging from \(L-\) at the appropriate place. Figure 4 represents the minimal solution for a single particle which enters the time-travel region from the left:

Figure 4: The Minimal Solution. [An extended description of figure 4 is in the supplement.]

The particle “travels back in time” three times. It is obvious that this minimal solution is a global solution, since the particle always travels inertially.

But the same initial state on \(S\) is also consistent with other global solutions. The new requirement imposed by the topology is just that the data going into \(L+\) from the bottom match the data coming out of \(L-\) from the top, and the data going into \(L-\) from the bottom match the data coming out of \(L+\) from the top. So we can add any number of vertical lines connecting \(L-\) and \(L+\) to a solution and still have a solution. For example, adding a few such lines to the minimal solution yields:

Figure 5: A Non-Minimal Solution. [An extended description of figure 5 is in the supplement.]

The particle now collides with itself twice: first before it reaches \(L+\) for the first time, and again shortly before it exits the CTC region. From the particle’s point of view, it is traveling to the right at a constant speed until it hits an older version of itself and comes to rest. It remains at rest until it is hit from the right by a younger version of itself, and then continues moving off, and the same process repeats later. It is clear that this is a global model of the dynamics, and that any number of distinct models could be generating by varying the number and placement of vertical lines.

Knowing the data on \(S\), then, gives us only incomplete information about how things will go for the particle. We know that the particle will enter the CTC region, and will reach \(L+\), we know that it will be the only particle in the universe, we know exactly where and with what speed it will exit the CTC region. But we cannot determine how many collisions the particle will undergo (if any), nor how long (in proper time) it will stay in the CTC region. If the particle were a clock, we could not predict what time it would indicate when exiting the region. Furthermore, the dynamics gives us no handle on what to think of the various possibilities: there are no probabilities assigned to the various distinct possible outcomes.

Changing the topology has changed the mathematics of the situation in two ways, which tend to pull in opposite directions. On the one hand, \(S\) is no longer a Cauchy surface, so it is perhaps not surprising that data on \(S\) do not suffice to fix a unique global solution. But on the other hand, there is an added constraint: data “coming out” of \(L-\) must exactly match data “going in” to \(L+\), even though what comes out of \(L-\) helps to determine what goes into \(L+\). This added consistency constraint tends to cut down on solutions, although in this case the additional constraint is more than outweighed by the freedom to consider various sorts of data on \({L+}/{L-}\).

The fact that the extra freedom outweighs the extra constraint also points up one unexpected way that the supposed paradoxes of time travel may be overcome. Let’s try to set up a paradoxical situation using the little closed time loop above. If we send a single particle into the loop from the left and do nothing else, we know exactly where it will exit the right side of the time travel region. Now suppose we station someone at the other side of the region with the following charge: if the particle should come out on the right side, the person is to do something to prevent the particle from going in on the left in the first place. In fact, this is quite easy to do: if we send a particle in from the right, it seems that it can exit on the left and deflect the incoming left-hand particle.

Carrying on our reflection in this way, we further realize that if the particle comes out on the right, we might as well send it back in order to deflect itself from entering in the first place. So all we really need to do is the following: set up a perfectly reflecting particle mirror on the right-hand side of the time travel region, and launch the particle from the left so that— if nothing interferes with it —it will just barely hit \(L+\). Our paradox is now apparently complete. If, on the one hand, nothing interferes with the particle it will enter the time-travel region on the left, exit on the right, be reflected from the mirror, re-enter from the right, and come out on the left to prevent itself from ever entering. So if it enters, it gets deflected and never enters. On the other hand, if it never enters then nothing goes in on the left, so nothing comes out on the right, so nothing is reflected back, and there is nothing to deflect it from entering. So if it doesn’t enter, then there is nothing to deflect it and it enters. If it enters, then it is deflected and doesn’t enter; if it doesn’t enter then there is nothing to deflect it and it enters: paradox complete.

But at least one solution to the supposed paradox is easy to construct: just follow the recipe for constructing the minimal solution, continuing the initial trajectory of the particle (reflecting it the mirror in the obvious way) and then read of the number and trajectories of the particles from the resulting diagram. We get the result of figure 6 :

Figure 6: Resolving the “Paradox”. [An extended description of figure 6 is in the supplement.]

As we can see, the particle approaching from the left never reaches \(L+\): it is deflected first by a particle which emerges from \(L-\). But it is not deflected by itself , as the paradox suggests, it is deflected by another particle. Indeed, there are now four particles in the diagram: the original particle and three particles which are confined to closed time-like curves. It is not the leftmost particle which is reflected by the mirror, nor even the particle which deflects the leftmost particle; it is another particle altogether.

The paradox gets it traction from an incorrect presupposition. If there is only one particle in the world at \(S\) then there is only one particle which could participate in an interaction in the time travel region: the single particle would have to interact with its earlier (or later) self. But there is no telling what might come out of \(L-\): the only requirement is that whatever comes out must match what goes in at \(L+\). So if you go to the trouble of constructing a working time machine, you should be prepared for a different kind of disappointment when you attempt to go back and kill yourself: you may be prevented from entering the machine in the first place by some completely unpredictable entity which emerges from it. And once again a peculiar sort of indeterminism appears: if there are many self-consistent things which could prevent you from entering, there is no telling which is even likely to materialize. This is just like the case of the unwritten book: the book is never written, so nothing determines what fills its pages.

So when the freedom to put data on \(L-\) outweighs the constraint that the same data go into \(L+\), instead of paradox we get an embarrassment of riches: many solution consistent with the data on \(S\), or many possible books. To see a case where the constraint “outweighs” the freedom, we need to construct a very particular, and frankly artificial, dynamics and topology. Consider the space of all linear dynamics for a scalar field on a lattice. (The lattice can be though of as a simple discrete space-time.) We will depict the space-time lattice as a directed graph. There is to be a scalar field defined at every node of the graph, whose value at a given node depends linearly on the values of the field at nodes which have arrows which lead to it. Each edge of the graph can be assigned a weighting factor which determines how much the field at the input node contributes to the field at the output node. If we name the nodes by the letters a , b , c , etc., and the edges by their endpoints in the obvious way, then we can label the weighting factors by the edges they are associated with in an equally obvious way.

Suppose that the graph of the space-time lattice is acyclic , as in figure 7 . (A graph is Acyclic if one can not travel in the direction of the arrows and go in a loop.)

Figure 7: An Acyclic Lattice. [An extended description of figure 7 is in the supplement.]

It is easy to regard a set of nodes as the analog of a Cauchy surface, e.g., the set \(\{a, b, c\}\), and it is obvious if arbitrary data are put on those nodes the data will generate a unique solution in the future. [ 3 ] If the value of the field at node \(a\) is 3 and at node \(b\) is 7, then its value at node \(d\) will be \(3W_{ad}\) and its value at node \(e\) will be \(3W_{ae} + 7W_{be}\). By varying the weighting factors we can adjust the dynamics, but in an acyclic graph the future evolution of the field will always be unique.

Let us now again artificially alter the topology of the lattice to admit CTCs, so that the graph now is cyclic. One of the simplest such graphs is depicted in figure 8 : there are now paths which lead from \(z\) back to itself, e.g., \(z\) to \(y\) to \(z\).

Figure 8: Time Travel on a Lattice. [An extended description of figure 8 is in the supplement.]

Can we now put arbitrary data on \(v\) and \(w\), and continue that data to a global solution? Will the solution be unique?

In the generic case, there will be a solution and the solution will be unique. The equations for the value of the field at \(x, y\), and \(z\) are:

Solving these equations for \(z\) yields

which gives a unique value for \(z\) in the generic case. But looking at the space of all possible dynamics for this lattice (i.e., the space of all possible weighting factors), we find a singularity in the case where \(1-W_{zx}W_{xz} - W_{zy}W_{yz} = 0\). If we choose weighting factors in just this way, then arbitrary data at \(v\) and \(w\) cannot be continued to a global solution. Indeed, if the scalar field is everywhere non-negative, then this particular choice of dynamics puts ironclad constraints on the value of the field at \(v\) and \(w\): the field there must be zero (assuming \(W_{vx}\) and \(W_{wy}\) to be non-zero), and similarly all nodes in their past must have field value zero. If the field can take negative values, then the values at \(v\) and \(w\) must be so chosen that \(vW_{vx}W_{xz} = -wW_{wy}W_{yz}\). In either case, the field values at \(v\) and \(w\) are severely constrained by the existence of the CTC region even though these nodes lie completely to the past of that region. It is this sort of constraint which we find to be unlike anything which appears in standard physics.

Our toy models suggest three things. The first is that it may be impossible to prove in complete generality that arbitrary data on a partial Cauchy surface can always be continued to a global solution: our artificial case provides an example where it cannot. The second is that such odd constraints are not likely to be generic: we had to delicately fine-tune the dynamics to get a problem. The third is that the opposite problem, namely data on a partial Cauchy surface being consistent with many different global solutions, is likely to be generic: we did not have to do any fine-tuning to get this result.

This third point leads to a peculiar sort of indeterminism, illustrated by the case of the unwritten book: the entire state on \(S\) does not determine what will happen in the future even though the local dynamics is deterministic and there are no other “edges” to space-time from which data could influence the result. What happens in the time travel region is constrained but not determined by what happens on \(S\), and the dynamics does not even supply any probabilities for the various possibilities. The example of the photographic negative discussed in section 2, then, seems likely to be unusual, for in that case there is a unique fixed point for the dynamics, and the set-up plus the dynamical laws determine the outcome. In the generic case one would rather expect multiple fixed points, with no room for anything to influence, even probabilistically, which would be realized. (See the supplement on

Remarks and Limitations on the Toy Models .

It is ironic that time travel should lead generically not to contradictions or to constraints (in the normal region) but to underdetermination of what happens in the time travel region by what happens everywhere else (an underdetermination tied neither to a probabilistic dynamics nor to a free edge to space-time). The traditional objection to time travel is that it leads to contradictions: there is no consistent way to complete an arbitrarily constructed story about how the time traveler intends to act. Instead, though, it appears that the more significant problem is underdetermination: the story can be consistently completed in many different ways.

Echeverria, Klinkhammer, and Thorne (1991) considered the case of 3-dimensional single hard spherical ball that can go through a single time travel wormhole so as to collide with its younger self.

Figure 9 [An extended description of figure 9 is in the supplement.]

The threat of paradox in this case arises in the following form. Consider the initial trajectory of a ball as it approaches the time travel region. For some initial trajectories, the ball does not undergo a collision before reaching mouth 1, but upon exiting mouth 2 it will collide with its earlier self. This leads to a contradiction if the collision is strong enough to knock the ball off its trajectory and deflect it from entering mouth 1. Of course, the Wheeler-Feynman strategy is to look for a “glancing blow” solution: a collision which will produce exactly the (small) deviation in trajectory of the earlier ball that produces exactly that collision. Are there always such solutions? [ 4 ]

Echeverria, Klinkhammer & Thorne found a large class of initial trajectories that have consistent “glancing blow” continuations, and found none that do not (but their search was not completely general). They did not produce a rigorous proof that every initial trajectory has a consistent continuation, but suggested that it is very plausible that every initial trajectory has a consistent continuation. That is to say, they have made it very plausible that, in the billiard ball wormhole case, the time travel structure of such a wormhole space-time does not result in constraints on states on spacelike surfaces in the non-time travel region.

In fact, as one might expect from our discussion in the previous section, they found the opposite problem from that of inconsistency: they found underdetermination. For a large class of initial trajectories there are multiple different consistent “glancing blow” continuations of that trajectory (many of which involve multiple wormhole traversals). For example, if one initially has a ball that is traveling on a trajectory aimed straight between the two mouths, then one obvious solution is that the ball passes between the two mouths and never time travels. But another solution is that the younger ball gets knocked into mouth 1 exactly so as to come out of mouth 2 and produce that collision. Echeverria et al. do not note the possibility (which we pointed out in the previous section) of the existence of additional balls in the time travel region. We conjecture (but have no proof) that for every initial trajectory of \(A\) there are some, and generically many, multiple-ball continuations.

Friedman, Morris, et al. (1990) examined the case of source-free non-self-interacting scalar fields traveling through such a time travel wormhole and found that no constraints on initial conditions in the non-time travel region are imposed by the existence of such time travel wormholes. In general there appear to be no known counter examples to the claim that in “somewhat realistic” time-travel space-times with a partial Cauchy surface there are no constraints imposed on the state on such a partial Cauchy surface by the existence of CTC’s. (See, e.g., Friedman & Morris 1991; Thorne 1994; Earman 1995; Earman, Smeenk, & Wüthrich 2009; and Dowe 2007.)

How about the issue of constraints in the time travel region \(T\)? Prima facie , constraints in such a region would not appear to be surprising. But one might still expect that there should be no constraints on states on a spacelike surface, provided one keeps the surface “small enough”. In the physics literature the following question has been asked: for any point \(p\) in \(T\), and any space-like surface \(S\) that includes \(p\) is there a neighborhood \(E\) of \(p\) in \(S\) such that any solution on \(E\) can be extended to a solution on the whole space-time? With respect to this question, there are some simple models in which one has this kind of extendability of local solutions to global ones, and some simple models in which one does not have such extendability, with no clear general pattern. The technical mathematical problems are amplified by the more conceptual problem of what it might mean to say that one could create a situation which forces the creation of closed timelike curves. (See, e.g., Yurtsever 1990; Friedman, Morris, et al. 1990; Novikov 1992; Earman 1995; and Earman, Smeenk, & Wüthrich 2009). What are we to think of all of this?

The toy models above all treat billiard balls, fields, and other objects propagating through a background spacetime with CTCs. Even if we can show that a consistent solution exists, there is a further question: what kind of matter and dynamics could generate CTCs to begin with? There are various solutions of Einstein’s equations with CTCs, but how do these exotic spacetimes relate to the models actually used in describing the world? In other words, what positive reasons might we have to take CTCs seriously as a feature of the actual universe, rather than an exotic possibility of primarily mathematical interest?

We should distinguish two different kinds of “possibility” that we might have in mind in posing such questions (following Stein 1970). First, we can consider a solution as a candidate cosmological model, describing the (large-scale gravitational degrees of freedom of the) entire universe. The case for ruling out spacetimes with CTCs as potential cosmological models strikes us as, surprisingly, fairly weak. Physicists used to simply rule out solutions with CTCs as unreasonable by fiat, due to the threat of paradoxes, which we have dismantled above. But it is also challenging to make an observational case. Observations tell us very little about global features, such as the existence of CTCs, because signals can only reach an observer from a limited region of spacetime, called the past light cone. Our past light cone—and indeed the collection of all the past light cones for possible observers in a given spacetime—can be embedded in spacetimes with quite different global features (Malament 1977, Manchak 2009). This undercuts the possibility of using observations to constrain global topology, including (among other things) ruling out the existence of CTCs.

Yet the case in favor of taking cosmological models with CTCs seriously is also not particularly strong. Some solutions used to describe black holes, which are clearly relevant in a variety of astrophysical contexts, include CTCs. But the question of whether the CTCs themselves play an essential representational role is subtle: the CTCs arise in the maximal extensions of these solutions, and can plausibly be regarded as extraneous to successful applications. Furthermore, many of the known solutions with CTCs have symmetries, raising the possibility that CTCs are not a stable or robust feature. Slight departures from symmetry may lead to a solution without CTCs, suggesting that the CTCs may be an artifact of an idealized model.

The second sense of possibility regards whether “reasonable” initial conditions can be shown to lead to, or not to lead to, the formation of CTCs. As with the toy models above, suppose that we have a partial Cauchy surface \(S\), such that all the temporal funny business lies to the future. Rather than simply assuming that there is a region with CTCs to the future, we can ask instead whether it is possible to create CTCs by manipulating matter in the initial, well-behaved region—that is, whether it is possible to build a time machine. Several physicists have pursued “chronology protection theorems” aiming to show that the dynamics of general relativity (or some other aspects of physics) rules this out, and to clarify why this is the case. The proof of such a theorem would justify neglecting solutions with CTCs as a source of insight into the nature of time in the actual world. But as of yet there are several partial results that do not fully settle the question. One further intriguing possibility is that even if general relativity by itself does protect chronology, it may not be possible to formulate a sensible theory describing matter and fields in solutions with CTCs. (See SEP entry on Time Machines; Smeenk and Wüthrich 2011 for more.)

There is a different question regarding the limitations of these toy models. The toy models and related examples show that there are consistent solutions for simple systems in the presence of CTCs. As usual we have made the analysis tractable by building toy models, selecting only a few dynamical degrees of freedom and tracking their evolution. But there is a large gap between the systems we have described and the time travel stories they evoke, with Kurt traveling along a CTC with murderous intentions. In particular, many features of the manifest image of time are tied to the thermodynamical properties of macroscopic systems. Rovelli (unpublished) considers a extremely simple system to illustrate the problem: can a clock move along a CTC? A clock consists of something in periodic motion, such as a pendulum bob, and something that counts the oscillations, such as an escapement mechanism. The escapement mechanism cannot work without friction; this requires dissipation and increasing entropy. For a clock that counts oscillations as it moves along a time-like trajectory, the entropy must be a monotonically increasing function. But that is obviously incompatible with the clock returning to precisely the same state at some future time as it completes a loop. The point generalizes, obviously, to imply that anything like a human, with memory and agency, cannot move along a CTC.

Since it is not obvious that one can rid oneself of all constraints in realistic models, let us examine the argument that time travel is implausible, and we should think it unlikely to exist in our world, in so far as it implies such constraints. The argument goes something like the following. In order to satisfy such constraints one needs some pre-established divine harmony between the global (time travel) structure of space-time and the distribution of particles and fields on space-like surfaces in it. But it is not plausible that the actual world, or any world even remotely like ours, is constructed with divine harmony as part of the plan. In fact, one might argue, we have empirical evidence that conditions in any spatial region can vary quite arbitrarily. So we have evidence that such constraints, whatever they are, do not in fact exist in our world. So we have evidence that there are no closed time-like lines in our world or one remotely like it. We will now examine this argument in more detail by presenting four possible responses, with counterresponses, to this argument.

Response 1. There is nothing implausible or new about such constraints. For instance, if the universe is spatially closed, there has to be enough matter to produce the needed curvature, and this puts constraints on the matter distribution on a space-like hypersurface. Thus global space-time structure can quite unproblematically constrain matter distributions on space-like hypersurfaces in it. Moreover we have no realistic idea what these constraints look like, so we hardly can be said to have evidence that they do not obtain.

Counterresponse 1. Of course there are constraining relations between the global structure of space-time and the matter in it. The Einstein equations relate curvature of the manifold to the matter distribution in it. But what is so strange and implausible about the constraints imposed by the existence of closed time-like curves is that these constraints in essence have nothing to do with the Einstein equations. When investigating such constraints one typically treats the particles and/or field in question as test particles and/or fields in a given space-time, i.e., they are assumed not to affect the metric of space-time in any way. In typical space-times without closed time-like curves this means that one has, in essence, complete freedom of matter distribution on a space-like hypersurface. (See response 2 for some more discussion of this issue). The constraints imposed by the possibility of time travel have a quite different origin and are implausible. In the ordinary case there is a causal interaction between matter and space-time that results in relations between global structure of space-time and the matter distribution in it. In the time travel case there is no such causal story to be told: there simply has to be some pre-established harmony between the global space-time structure and the matter distribution on some space-like surfaces. This is implausible.

Response 2. Constraints upon matter distributions are nothing new. For instance, Maxwell’s equations constrain electric fields \(\boldsymbol{E}\) on an initial surface to be related to the (simultaneous) charge density distribution \(\varrho\) by the equation \(\varrho = \text{div}(\boldsymbol{E})\). (If we assume that the \(E\) field is generated solely by the charge distribution, this conditions amounts to requiring that the \(E\) field at any point in space simply be the one generated by the charge distribution according to Coulomb’s inverse square law of electrostatics.) This is not implausible divine harmony. Such constraints can hold as a matter of physical law. Moreover, if we had inferred from the apparent free variation of conditions on spatial regions that there could be no such constraints we would have mistakenly inferred that \(\varrho = \text{div}(\boldsymbol{E})\) could not be a law of nature.

Counterresponse 2. The constraints imposed by the existence of closed time-like lines are of quite a different character from the constraint imposed by \(\varrho = \text{div}(\boldsymbol{E})\). The constraints imposed by \(\varrho = \text{div}(\boldsymbol{E})\) on the state on a space-like hypersurface are:

• local constraints (i.e., to check whether the constraint holds in a region you just need to see whether it holds at each point in the region),
• quite independent of the global space-time structure,
• quite independent of how the space-like surface in question is embedded in a given space-time, and
• very simply and generally stateable.

On the other hand, the consistency constraints imposed by the existence of closed time-like curves (i) are not local, (ii) are dependent on the global structure of space-time, (iii) depend on the location of the space-like surface in question in a given space-time, and (iv) appear not to be simply stateable other than as the demand that the state on that space-like surface embedded in such and such a way in a given space-time, do not lead to inconsistency. On some views of laws (e.g., David Lewis’ view) this plausibly implies that such constraints, even if they hold, could not possibly be laws. But even if one does not accept such a view of laws, one could claim that the bizarre features of such constraints imply that it is implausible that such constraints hold in our world or in any world remotely like ours.

Response 3. It would be strange if there are constraints in the non-time travel region. It is not strange if there are constraints in the time travel region. They should be explained in terms of the strange, self-interactive, character of time travel regions. In this region there are time-like trajectories from points to themselves. Thus the state at such a point, in such a region, will, in a sense, interact with itself. It is a well-known fact that systems that interact with themselves will develop into an equilibrium state, if there is such an equilibrium state, or else will develop towards some singularity. Normally, of course, self-interaction isn’t true instantaneous self-interaction, but consists of a feed-back mechanism that takes time. But in time travel regions something like true instantaneous self-interaction occurs. This explains why constraints on states occur in such time travel regions: the states “ ab initio ” have to be “equilibrium states”. Indeed in a way this also provides some picture of why indeterminism occurs in time travel regions: at the onset of self-interaction states can fork into different equi-possible equilibrium states.

Counterresponse 3. This is explanation by woolly analogy. It all goes to show that time travel leads to such bizarre consequences that it is unlikely that it occurs in a world remotely like ours.

Response 4. All of the previous discussion completely misses the point. So far we have been taking the space-time structure as given, and asked the question whether a given time travel space-time structure imposes constraints on states on (parts of) space-like surfaces. However, space-time and matter interact. Suppose that one is in a space-time with closed time-like lines, such that certain counterfactual distributions of matter on some neighborhood of a point \(p\) are ruled out if one holds that space-time structure fixed. One might then ask

Why does the actual state near \(p\) in fact satisfy these constraints? By what divine luck or plan is this local state compatible with the global space-time structure? What if conditions near \(p\) had been slightly different?

And one might take it that the lack of normal answers to these questions indicates that it is very implausible that our world, or any remotely like it, is such a time travel universe. However the proper response to these question is the following. There are no constraints in any significant sense. If they hold they hold as a matter of accidental fact, not of law. There is no more explanation of them possible than there is of any contingent fact. Had conditions in a neighborhood of \(p\) been otherwise, the global structure of space-time would have been different. So what? The only question relevant to the issue of constraints is whether an arbitrary state on an arbitrary spatial surface \(S\) can always be embedded into a space-time such that that state on \(S\) consistently extends to a solution on the entire space-time.

But we know the answer to that question. A well-known theorem in general relativity says the following: any initial data set on a three dimensional manifold \(S\) with positive definite metric has a unique embedding into a maximal space-time in which \(S\) is a Cauchy surface (see, e.g., Geroch & Horowitz 1979: 284 for more detail), i.e., there is a unique largest space-time which has \(S\) as a Cauchy surface and contains a consistent evolution of the initial value data on \(S\). Now since \(S\) is a Cauchy surface this space-time does not have closed time like curves. But it may have extensions (in which \(S\) is not a Cauchy surface) which include closed timelike curves, indeed it may be that any maximal extension of it would include closed timelike curves. (This appears to be the case for extensions of states on certain surfaces of Taub-NUT space-times. See Earman, Smeenk, & Wüthrich 2009). But these extensions, of course, will be consistent. So properly speaking, there are no constraints on states on space-like surfaces. Nonetheless the space-time in which these are embedded may or may not include closed time-like curves.

Counterresponse 4. This, in essence, is the stonewalling answer which we indicated in section 1. However, whether or not you call the constraints imposed by a given space-time on distributions of matter on certain space-like surfaces “genuine constraints”, whether or not they can be considered lawlike, and whether or not they need to be explained, the existence of such constraints can still be used to argue that time travel worlds are so bizarre that it is implausible that our world or any world remotely like ours is a time travel world.

Suppose that one is in a time travel world. Suppose that given the global space-time structure of this world, there are constraints imposed upon, say, the state of motion of a ball on some space-like surface when it is treated as a test particle, i.e., when it is assumed that the ball does not affect the metric properties of the space-time it is in. (There is lots of other matter that, via the Einstein equation, corresponds exactly to the curvature that there is everywhere in this time travel worlds.) Now a real ball of course does have some effect on the metric of the space-time it is in. But let us consider a ball that is so small that its effect on the metric is negligible. Presumably it will still be the case that certain states of this ball on that space-like surface are not compatible with the global time travel structure of this universe.

This means that the actual distribution of matter on such a space-like surface can be extended into a space-time with closed time-like lines, but that certain counterfactual distributions of matter on this space-like surface can not be extended into the same space-time. But note that the changes made in the matter distribution (when going from the actual to the counterfactual distribution) do not in any non-negligible way affect the metric properties of the space-time. (Recall that the changes only effect test particles.) Thus the reason why the global time travel properties of the counterfactual space-time have to be significantly different from the actual space-time is not that there are problems with metric singularities or alterations in the metric that force significant global changes when we go to the counterfactual matter distribution. The reason that the counterfactual space-time has to be different is that in the counterfactual world the ball’s initial state of motion starting on the space-like surface, could not “meet up” in a consistent way with its earlier self (could not be consistently extended) if we were to let the global structure of the counterfactual space-time be the same as that of the actual space-time. Now, it is not bizarre or implausible that there is a counterfactual dependence of manifold structure, even of its topology, on matter distributions on spacelike surfaces. For instance, certain matter distributions may lead to singularities, others may not. We may indeed in some sense have causal power over the topology of the space-time we live in. But this power normally comes via the Einstein equations. But it is bizarre to think that there could be a counterfactual dependence of global space-time structure on the arrangement of certain tiny bits of matter on some space-like surface, where changes in that arrangement by assumption do not affect the metric anywhere in space-time in any significant way . It is implausible that we live in such a world, or that a world even remotely like ours is like that.

Let us illustrate this argument in a different way by assuming that wormhole time travel imposes constraints upon the states of people prior to such time travel, where the people have so little mass/energy that they have negligible effect, via the Einstein equation, on the local metric properties of space-time. Do you think it more plausible that we live in a world where wormhole time travel occurs but it only occurs when people’s states are such that these local states happen to combine with time travel in such a way that nobody ever succeeds in killing their younger self, or do you think it more plausible that we are not in a wormhole time travel world? [ 5 ]

An alternative approach to time travel (initiated by Deutsch 1991) abstracts away from the idealized toy models described above. [ 6 ] This computational approach considers instead the evolution of bits (simple physical systems with two discrete states) through a network of interactions, which can be represented by a circuit diagram with gates corresponding to the interactions. Motivated by the possibility of CTCs, Deutsch proposed adding a new kind of channel that connects the output of a given gate back to its input —in essence, a backwards-time step. More concretely, given a gate that takes \(n\) bits as input, we can imagine taking some number \(i \lt n\) of these bits through a channel that loops back and then do double-duty as inputs. Consistency requires that the state of these \(i\) bits is the same for output and input. (We will consider an illustration of this kind of system in the next section.) Working through examples of circuit diagrams with a CTC channel leads to similar treatments of Consistency and Underdetermination as the discussion above (see, e.g., Wallace 2012: § 10.6). But the approach offers two new insights (both originally due to Deutsch): the Easy Knowledge paradox, and a particularly clear extension to time travel in quantum mechanics.

A computer equipped with a CTC channel can exploit the need to find consistent evolution to solve remarkably hard problems. (This is quite different than the first idea that comes to mind to enhance computational power: namely to just devote more time to a computation, and then send the result back on the CTC to an earlier state.) The gate in a circuit incorporating a CTC implements a function from the input bits to the output bits, under the constraint that the output and input match the i bits going through the CTC channel. This requires, in effect, finding the fixed point of the relevant function. Given the generality of the model, there are few limits on the functions that could be implemented on the CTC circuit. Nature has to solve a hard computational problem just to ensure consistent evolution. This can then be extended to other complex computational problems—leading, more precisely, to solutions of NP -complete problems in polynomial time (see Aaronson 2013: Chapter 20 for an overview and further references). The limits imposed by computational complexity are an essential part of our epistemic situation, and computers with CTCs would radically change this.

We now turn to the application of the computational approach to the quantum physics of time travel (see Deutsch 1991; Deutsch & Lockwood 1994). By contrast with the earlier discussions of constraints in classical systems, they claim to show that time travel never imposes any constraints on the pre-time travel state of quantum systems. The essence of this account is as follows. [ 7 ]

A quantum system starts in state \(S_1\), interacts with its older self, after the interaction is in state \(S_2\), time travels while developing into state \(S_3\), then interacts with its younger self, and ends in state \(S_4\) (see figure 10 ).

Figure 10 [An extended description of figure 10 is in the supplement.]

Deutsch assumes that the set of possible states of this system are the mixed states, i.e., are represented by the density matrices over the Hilbert space of that system. Deutsch then shows that for any initial state \(S_1\), any unitary interaction between the older and younger self, and any unitary development during time travel, there is a consistent solution, i.e., there is at least one pair of states \(S_2\) and \(S_3\) such that when \(S_1\) interacts with \(S_3\) it will change to state \(S_2\) and \(S_2\) will then develop into \(S_3\). The states \(S_2, S_3\) and \(S_4\) will typically be not be pure states, i.e., will be non-trivial mixed states, even if \(S_1\) is pure. In order to understand how this leads to interpretational problems let us give an example. Consider a system that has a two dimensional Hilbert space with as a basis the states \(\vc{+}\) and \(\vc{-}\). Let us suppose that when state \(\vc{+}\) of the young system encounters state \(\vc{+}\) of the older system, they interact and the young system develops into state \(\vc{-}\) and the old system remains in state \(\vc{+}\). In obvious notation:

Similarly, suppose that:

Let us furthermore assume that there is no development of the state of the system during time travel, i.e., that \(\vc{+}_2\) develops into \(\vc{+}_3\), and that \(\vc{-}_2\) develops into \(\vc{-}_3\).

Now, if the only possible states of the system were \(\vc{+}\) and \(\vc{-}\) (i.e., if there were no superpositions or mixtures of these states), then there is a constraint on initial states: initial state \(\vc{+}_1\) is impossible. For if \(\vc{+}_1\) interacts with \(\vc{+}_3\) then it will develop into \(\vc{-}_2\), which, during time travel, will develop into \(\vc{-}_3\), which inconsistent with the assumed state \(\vc{+}_3\). Similarly if \(\vc{+}_1\) interacts with \(\vc{-}_3\) it will develop into \(\vc{+}_2\), which will then develop into \(\vc{+}_3\) which is also inconsistent. Thus the system can not start in state \(\vc{+}_1\).

But, says Deutsch, in quantum mechanics such a system can also be in any mixture of the states \(\vc{+}\) and \(\vc{-}\). Suppose that the older system, prior to the interaction, is in a state \(S_3\) which is an equal mixture of 50% \(\vc{+}_3\) and 50% \(\vc{-}_3\). Then the younger system during the interaction will develop into a mixture of 50% \(\vc{+}_2\) and 50% \(\vc{-}_2\), which will then develop into a mixture of 50% \(\vc{+}_3\) and 50% \(\vc{-}_3\), which is consistent! More generally Deutsch uses a fixed point theorem to show that no matter what the unitary development during interaction is, and no matter what the unitary development during time travel is, for any state \(S_1\) there is always a state \(S_3\) (which typically is not a pure state) which causes \(S_1\) to develop into a state \(S_2\) which develops into that state \(S_3\). Thus quantum mechanics comes to the rescue: it shows in all generality that no constraints on initial states are needed!

One might wonder why Deutsch appeals to mixed states: will superpositions of states \(\vc{+}\) and \(\vc{-}\) not suffice? Unfortunately such an idea does not work. Suppose again that the initial state is \(\vc{+}_1\). One might suggest that that if state \(S_3\) is

one will obtain a consistent development. For one might think that when initial state \(\vc{+}_1\) encounters the superposition

it will develop into superposition

and that this in turn will develop into

as desired. However this is not correct. For initial state \(\vc{+}_1\) when it encounters

will develop into the entangled state

In so far as one can speak of the state of the young system after this interaction, it is in the mixture of 50% \(\vc{+}_2\) and 50% \(\vc{-}_2\), not in the superposition

So Deutsch does need his recourse to mixed states.

This clarification of why Deutsch needs his mixtures does however indicate a serious worry about the simplifications that are part of Deutsch’s account. After the interaction the old and young system will (typically) be in an entangled state. Although for purposes of a measurement on one of the two systems one can say that this system is in a mixed state, one can not represent the full state of the two systems by specifying the mixed state of each separate part, as there are correlations between observables of the two systems that are not represented by these two mixed states, but are represented in the joint entangled state. But if there really is an entangled state of the old and young systems directly after the interaction, how is one to represent the subsequent development of this entangled state? Will the state of the younger system remain entangled with the state of the older system as the younger system time travels and the older system moves on into the future? On what space-like surfaces are we to imagine this total entangled state to be? At this point it becomes clear that there is no obvious and simple way to extend elementary non-relativistic quantum mechanics to space-times with closed time-like curves: we apparently need to characterize not just the entanglement between two systems, but entanglement relative to specific spacetime descriptions.

How does Deutsch avoid these complications? Deutsch assumes a mixed state \(S_3\) of the older system prior to the interaction with the younger system. He lets it interact with an arbitrary pure state \(S_1\) younger system. After this interaction there is an entangled state \(S'\) of the two systems. Deutsch computes the mixed state \(S_2\) of the younger system which is implied by this entangled state \(S'\). His demand for consistency then is just that this mixed state \(S_2\) develops into the mixed state \(S_3\). Now it is not at all clear that this is a legitimate way to simplify the problem of time travel in quantum mechanics. But even if we grant him this simplification there is a problem: how are we to understand these mixtures?

If we take an ignorance interpretation of mixtures we run into trouble. For suppose that we assume that in each individual case each older system is either in state \(\vc{+}_3\) or in state \(\vc{-}_3\) prior to the interaction. Then we regain our paradox. Deutsch instead recommends the following, many worlds, picture of mixtures. Suppose we start with state \(\vc{+}_1\) in all worlds. In some of the many worlds the older system will be in the \(\vc{+}_3\) state, let us call them A -worlds, and in some worlds, B -worlds, it will be in the \(\vc{-}_3\) state. Thus in A -worlds after interaction we will have state \(\vc{-}_2\) , and in B -worlds we will have state \(\vc{+}_2\). During time travel the \(\vc{-}_2\) state will remain the same, i.e., turn into state \(\vc{-}_3\), but the systems in question will travel from A -worlds to B -worlds. Similarly the \(\vc{+}\) \(_2\) states will travel from the B -worlds to the A -worlds, thus preserving consistency.

Now whatever one thinks of the merits of many worlds interpretations, and of this understanding of it applied to mixtures, in the end one does not obtain genuine time travel in Deutsch’s account. The systems in question travel from one time in one world to another time in another world, but no system travels to an earlier time in the same world. (This is so at least in the normal sense of the word “world”, the sense that one means when, for instance, one says “there was, and will be, only one Elvis Presley in this world.”) Thus, even if it were a reasonable view, it is not quite as interesting as it may have initially seemed. (See Wallace 2012 for a more sympathetic treatment, that explores several further implications of accepting time travel in conjunction with the many worlds interpretation.)

We close by acknowledging that Deutsch’s starting point—the claim that this computational model captures the essential features of quantum systems in a spacetime with CTCs—has been the subject of some debate. Several physicists have pursued a quite different treatment of evolution of quantum systems through CTC’s, based on considering the “post-selected” state (see Lloyd et al. 2011). Their motivations for implementing the consistency condition in terms of the post-selected state reflects a different stance towards quantum foundations. A different line of argument aims to determine whether Deutsch’s treatment holds as an appropriate limiting case of a more rigorous treatment, such as quantum field theory in curved spacetimes. For example, Verch (2020) establishes several results challenging the assumption that Deutsch’s treatment is tied to the presence of CTC’s, or that it is compatible with the entanglement structure of quantum fields.

What remains of the grandfather paradox in general relativistic time travel worlds is the fact that in some cases the states on edgeless spacelike surfaces are “overconstrained”, so that one has less than the usual freedom in specifying conditions on such a surface, given the time-travel structure, and in some cases such states are “underconstrained”, so that states on edgeless space-like surfaces do not determine what happens elsewhere in the way that they usually do, given the time travel structure. There can also be mixtures of those two types of cases. The extent to which states are overconstrained and/or underconstrained in realistic models is as yet unclear, though it would be very surprising if neither obtained. The extant literature has primarily focused on the problem of overconstraint, since that, often, either is regarded as a metaphysical obstacle to the possibility time travel, or as an epistemological obstacle to the plausibility of time travel in our world. While it is true that our world would be quite different from the way we normally think it is if states were overconstrained, underconstraint seems at least as bizarre as overconstraint. Nonetheless, neither directly rules out the possibility of time travel.

If time travel entailed contradictions then the issue would be settled. And indeed, most of the stories employing time travel in popular culture are logically incoherent: one cannot “change” the past to be different from what it was, since the past (like the present and the future) only occurs once. But if the only requirement demanded is logical coherence, then it seems all too easy. A clever author can devise a coherent time-travel scenario in which everything happens just once and in a consistent way. This is just too cheap: logical coherence is a very weak condition, and many things we take to be metaphysically impossible are logically coherent. For example, it involves no logical contradiction to suppose that water is not molecular, but if both chemistry and Kripke are right it is a metaphysical impossibility. We have been interested not in logical possibility but in physical possibility. But even so, our conditions have been relatively weak: we have asked only whether time-travel is consistent with the universal validity of certain fundamental physical laws and with the notion that the physical state on a surface prior to the time travel region be unconstrained. It is perfectly possible that the physical laws obey this condition, but still that time travel is not metaphysically possible because of the nature of time itself. Consider an analogy. Aristotle believed that water is homoiomerous and infinitely divisible: any bit of water could be subdivided, in principle, into smaller bits of water. Aristotle’s view contains no logical contradiction. It was certainly consistent with Aristotle’s conception of water that it be homoiomerous, so this was, for him, a conceptual possibility. But if chemistry is right, Aristotle was wrong both about what water is like and what is possible for it. It can’t be infinitely divided, even though no logical or conceptual analysis would reveal that.

Similarly, even if all of our consistency conditions can be met, it does not follow that time travel is physically possible, only that some specific physical considerations cannot rule it out. The only serious proof of the possibility of time travel would be a demonstration of its actuality. For if we agree that there is no actual time travel in our universe, the supposition that there might have been involves postulating a substantial difference from actuality, a difference unlike in kind from anything we could know if firsthand. It is unclear to us exactly what the content of possible would be if one were to either maintain or deny the possibility of time travel in these circumstances, unless one merely meant that the possibility is not ruled out by some delineated set of constraints. As the example of Aristotle’s theory of water shows, conceptual and logical “possibility” do not entail possibility in a full-blooded sense. What exactly such a full-blooded sense would be in case of time travel, and whether one could have reason to believe it to obtain, remain to us obscure.

• Aaronson, Scott, 2013, Quantum Computing since Democritus , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511979309
• Arntzenius, Frank, 2006, “Time Travel: Double Your Fun”, Philosophy Compass , 1(6): 599–616. doi:10.1111/j.1747-9991.2006.00045.x
• Clarke, C.J.S., 1977, “Time in General Relativity” in Foundations of Space-Time Theory , Minnesota Studies in the Philosophy of Science , Vol VIII, Earman, J., Glymour, C., and Stachel, J. (eds), pp. 94–108. Minneapolis: University of Minnesota Press.
• Deutsch, David, 1991, “Quantum Mechanics near Closed Timelike Lines”, Physical Review D , 44(10): 3197–3217. doi:10.1103/PhysRevD.44.3197
• Deutsch, David and Michael Lockwood, 1994, “The Quantum Physics of Time Travel”, Scientific American , 270(3): 68–74. doi:10.1038/scientificamerican0394-68
• Dowe, Phil, 2007, “Constraints on Data in Worlds with Closed Timelike Curves”, Philosophy of Science , 74(5): 724–735. doi:10.1086/525617
• Earman, John, 1972, “Implications of Causal Propagation Outside the Null Cone”, Australasian Journal of Philosophy , 50(3): 222–237. doi:10.1080/00048407212341281
• Earman, John, 1995, Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes , New York: Oxford University Press.
• Earman, John, Christopher Smeenk, and Christian Wüthrich, 2009, “Do the Laws of Physics Forbid the Operation of Time Machines?”, Synthese , 169(1): 91–124. doi:10.1007/s11229-008-9338-2
• Echeverria, Fernando, Gunnar Klinkhammer, and Kip S. Thorne, 1991, “Billiard Balls in Wormhole Spacetimes with Closed Timelike Curves: Classical Theory”, Physical Review D , 44(4): 1077–1099. doi:10.1103/PhysRevD.44.1077
• Effingham, Nikk, 2020, Time Travel: Probability and Impossibility , Oxford: Oxford University Press. doi:10.1093/oso/9780198842507.001.0001
• Fletcher, Samuel C., 2020, “The Principle of Stability”, Philosopher’s Imprint , 20: article 3. [ Fletcher 2020 available online ]
• Friedman, John and Michael Morris, 1991, “The Cauchy Problem for the Scalar Wave Equation Is Well Defined on a Class of Spacetimes with Closed Timelike Curves”, Physical Review Letters , 66(4): 401–404. doi:10.1103/PhysRevLett.66.401
• Friedman, John, Michael S. Morris, Igor D. Novikov, Fernando Echeverria, Gunnar Klinkhammer, Kip S. Thorne, and Ulvi Yurtsever, 1990, “Cauchy Problem in Spacetimes with Closed Timelike Curves”, Physical Review D , 42(6): 1915–1930. doi:10.1103/PhysRevD.42.1915
• Geroch, Robert and Gary Horowitz, 1979, “Global Structures of Spacetimes”, in General Relativity: An Einstein Centenary Survey , Stephen Hawking and W. Israel (eds.), Cambridge/New York: Cambridge University Press, Chapter 5, pp. 212–293.
• Gödel, Kurt, 1949, “A Remark About the Relationship Between Relativity Theory and Idealistic Philosophy”, in Albert Einstein, Philosopher-Scientist , Paul Arthur Schilpp (ed.), Evanston, IL: Library of Living Philosophers, 557–562.
• Hocking, John G. and Gail S. Young, 1961, Topology , (Addison-Wesley Series in Mathematics), Reading, MA: Addison-Wesley.
• Horwich, Paul, 1987, “Time Travel”, in his Asymmetries in Time: Problems in the Philosophy of Science , , Cambridge, MA: MIT Press, 111–128.
• Kutach, Douglas N., 2003, “Time Travel and Consistency Constraints”, Philosophy of Science , 70(5): 1098–1113. doi:10.1086/377392
• Lewis, David, 1976, “The Paradoxes of Time Travel”, American Philosophical Quarterly , 13(2): 145–152.
• Lloyd, Seth, Lorenzo Maccone, Raul Garcia-Patron, Vittorio Giovannetti, and Yutaka Shikano, 2011, “Quantum Mechanics of Time Travel through Post-Selected Teleportation”, Physical Review D , 84(2): 025007. doi:10.1103/PhysRevD.84.025007
• Malament, David B., 1977, “Observationally Indistinguishable Spacetimes: Comments on Glymour’s Paper”, in Foundations of Space-Time Theories , John Earman, Clark N. Glymour, and John J. Stachel (eds.), (Minnesota Studies in the Philosophy of Science 8), Minneapolis, MN: University of Minnesota Press, 61–80.
• –––, 1984, “‘Time Travel’ in the Gödel Universe”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1984(2): 91–100. doi:10.1086/psaprocbienmeetp.1984.2.192497
• –––, 1985, “Minimal Acceleration Requirements for ‘Time Travel’, in Gödel Space‐time”, Journal of Mathematical Physics , 26(4): 774–777. doi:10.1063/1.526566
• Manchak, John Byron, 2009, “Can We Know the Global Structure of Spacetime?”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 40(1): 53–56. doi:10.1016/j.shpsb.2008.07.004
• –––, 2011, “On Efficient ‘Time Travel’ in Gödel Spacetime”, General Relativity and Gravitation , 43(1): 51–60. doi:10.1007/s10714-010-1068-3
• Maudlin, Tim, 1990, “Time-Travel and Topology”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1990(1): 303–315. doi:10.1086/psaprocbienmeetp.1990.1.192712
• Novikov, I. D., 1992, “Time Machine and Self-Consistent Evolution in Problems with Self-Interaction”, Physical Review D , 45(6): 1989–1994. doi:10.1103/PhysRevD.45.1989
• Smeenk, Chris and Christian Wüthrich, 2011, “Time Travel and Time Machines”, in the Oxford Handbook on Time , Craig Callender (ed.), Oxford: Oxford University Press, 577–630..
• Stein, Howard, 1970, “On the Paradoxical Time-Structures of Gödel”, Philosophy of Science , 37(4): 589–601. doi:10.1086/288328
• Thorne, Kip S., 1994, Black Holes and Time Warps: Einstein’s Outrageous Legacy , (Commonwealth Fund Book Program), New York: W.W. Norton.
• Verch, Rainer, 2020, “The D-CTC Condition in Quantum Field Theory”, in Progress and Visions in Quantum Theory in View of Gravity , Felix Finster, Domenico Giulini, Johannes Kleiner, and Jürgen Tolksdorf (eds.), Cham: Springer International Publishing, 221–232. doi:10.1007/978-3-030-38941-3_9
• Wallace, David, 2012, The Emergent Multiverse: Quantum Theory According to the Everett Interpretation , Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780199546961.001.0001
• Wasserman, Ryan, 2018, Paradoxes of Time Travel , Oxford: Oxford University Press. doi:10.1093/oso/9780198793335.001.0001
• Weyl, Hermann, 1918/1920 [1922/1952], Raum, Zeit, Materie , Berlin: Springer; fourth edition 1920. Translated as Space—Time—Matter , Henry Leopold Brose (trans.), New York: Dutton, 1922. Reprinted 1952, New York: Dover Publications.
• Wheeler, John Archibald and Richard Phillips Feynman, 1949, “Classical Electrodynamics in Terms of Direct Interparticle Action”, Reviews of Modern Physics , 21(3): 425–433. doi:10.1103/RevModPhys.21.425
• Yurtsever, Ulvi, 1990, “Test Fields on Compact Space‐times”, Journal of Mathematical Physics , 31(12): 3064–3078. doi:10.1063/1.528960

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• Adlam, Emily, unpublished, “ Is There Causation in Fundamental Physics? New Insights from Process Matrices and Quantum Causal Modelling ”, 2022, arXiv: 2208.02721. doi:10.48550/ARXIV.2208.02721
• Rovelli, Carlo, unpublished, “ Can We Travel to the Past? Irreversible Physics along Closed Timelike Curves ”, arXiv: 1912.04702. doi:10.48550/ARXIV.1912.04702

causation: backward | determinism: causal | quantum mechanics | quantum mechanics: retrocausality | space and time: being and becoming in modern physics | time machines | time travel

Copyright © 2023 by Christopher Smeenk < csmeenk2 @ uwo . ca > Frank Arntzenius Tim Maudlin

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

Scientists use quantum entanglement to travel in time

“these simulations do not allow you to go back and alter your past, but they do allow you to create a better tomorrow by fixing yesterday’s problems today.”.

Loukia Papadopoulos

Representational image of time travel.

DKosig/iStock  

Researchers at the University of Cambridge have demonstrated that they can mimic what would happen if one could travel back in time by playing with entanglement, a central concept in quantum mechanics that allows particles to be inherently linked.

Quantum entanglement is an intriguing phenomenon that occurs when two or more particles become correlated in such a way that the state of one particle cannot be described independently of the state of the other(s), even when they are separated by large distances. This means that the properties of one particle, such as its spin or polarization, are dependent on the properties of the other particle(s).

A gift from the past

“Imagine that you want to send a gift to someone: you need to send it on day one to make sure it arrives on day three,” said lead author David Arvidsson-Shukur, from the Hitachi Cambridge Laboratory. “However, you only receive that person’s wish list on day two. So, in this chronology-respecting scenario, it’s impossible for you to know in advance what they will want as a gift and to make sure you send the right one.

“Now imagine you can change what you send on day one with the information from the wish list received on day two. Our simulation uses quantum entanglement manipulation to show how you could retroactively change your previous actions to ensure the final outcome is the one you want.”

Entanglement’s ability to instantly reflect changes in one particle’s state in another particle’s state independent of their physical proximity is one of its most remarkable features. Albert Einstein is credited with using the phrase “spooky action at a distance” to describe what appears to be happening. Due to the fact that two particles can continue to interact even when separated, quantum physics offers a unique solution to time travel.

Co-author Nicole Yunger Halpern, researcher at the National Institute of Standards and Technology (NIST) and the University of Maryland, explained that what the scientists are proposing is the entanglement of two particles.

The first particle is the one used in an experiment. It then acquires new information which leads the experimentalist to manipulate the second particle to effectively alter the first particle’s past state. This process then changes the outcome of the experiment, linking the past to the present.

Linking quantum metrology

The theorists then linked quantum metrology to their model to make it relevant to technology. A common quantum metrology experiment involves shining photons onto an object of interest, and then subsequently registering them with a unique kind of camera. The photons must be prepared in a specific way before they reach the sample for this experiment to be effective. The scientists demonstrated that even if they discover the optimum way to prepare the photons after they have already reached the sample, they can still utilize simulations of time travel to alter the original photons.

RECOMMENDED ARTICLES

“We are not proposing a time travel machine, but rather a deep dive into the fundamentals of quantum mechanics. These simulations do not allow you to go back and alter your past, but they do allow you to create a better tomorrow by fixing yesterday’s problems today,” said Arvidsson-Shukur.

The Blueprint Daily

Stay up-to-date on engineering, tech, space, and science news with The Blueprint.

By clicking sign up, you confirm that you accept this site's Terms of Use and Privacy Policy

ABOUT THE EDITOR

Loukia Papadopoulos <p>Loukia Papadopoulos is a journalist, writer, and editor with previous experience with the United Nations Momentum for Change, Leo Burnett and Al Arabiya English. She holds a D.E.C. in Pure and Applied Sciences from Marianopolis College, a B.A. in Communications and an M.Sc. in Geography, Urban and Environmental Studies from Concordia University.</p>

FEATURED VIDEO

Popular articles, mouthpad: paralyzed people can now control phones, pcs with their tongues, poop balloon war continues: south korea airdrops k-pop usbs on n. korea, first crewed boeing starliner mission lifts off successfully, heads to iss, ‘failed’ solar eruption reveals sun’s powerful gravitational pull, related articles.

Starship soars around Earth once again, survives hypersonic reentry

Humanoid tourist: Watch AI-powered robot climb the Great Wall of China

Tree-based batteries to power Europe’s fight against China’s lithium dominance

China: World’s first 3D e-skin gives robots human-like touching sense

• Collections

• APS Journals

Time Travel without Regrets

Time travel is not ruled out by general relativity, but it might well create problems for the laws of common sense. In the 28 January Physical Review Letters , a team proposes a new way of deciding the possibility or impossibility of quantum states that travel forward and backward in time. The new criterion automatically disallows quantum versions of the “grandfather paradox,” in which a person travels back in time and kills her ancestor, thereby ensuring her own demise. The team also performed an experiment that illustrates the paradox-nullifying mechanism.

General relativity, Einstein’s theory of space and time, allows the existence of closed timelike curves (CTCs)–paths that go forward in time, then back again to reconnect and form closed loops. Although it’s unclear whether CTCs can be created, physicists have nevertheless explored their possible consequences, including their influence on quantum mechanics.

An ordinary quantum event might involve two particles moving forward in time, changing each other by interacting at some time, then going their separate ways into the future. However, if one outgoing particle enters a CTC, it can double back and become one of the ingoing particles–thus influencing its own transformation. In 1991, Oxford University physicist David Deutsch proposed a consistency condition to avoid time-travel paradoxes: a particle that loops back in time in this way should be in the same quantum state when in reappears in the immediate past of the interaction as it was when it departed the interaction for the immediate future [1] .

To see how this condition works, imagine a quantum particle having states labeled 0 and 1. It travels around a CTC and, on its return, interacts with an “external” particle in such a way that 0 becomes 1 and 1 becomes 0. Such a particle presents a quantum grandfather paradox: when it comes back around the loop, it flips its former self to the opposite state. However, Deutsch showed that consistency is possible if the particle is in a superposition–a state that is equal parts 0 and 1. The interaction exchanges the 0 and the 1, but the state overall remains unchanged. For this to work, the external particle must also be in a superposition that flips back and forth.

The paradox is avoided, but a difficulty arises if the external particle is measured. Then it cannot remain in a superposition but must become definitely either 0 or 1–which means that the CTC particle cannot remain in a superposition, either. To preserve consistency, Deutsch argued that the CTC particle must exist in two parallel universes–the “1-universe” and the “0-universe”–and continually switch between them, so that no contradiction occurs in either one.

Lorenzo Maccone, of the Massachusetts Institute of Technology and the University of Pavia, Italy, and his colleagues propose a more stringent condition that avoids these difficulties. They require that any measurement of the particle going into the future should yield the same result as measuring it when it returns from the past. So any state that would alter the past when it came around again is disallowed, and no grandfather-type paradoxes can arise.

Perhaps surprisingly, “we can still have CTCs even with this strong condition,” Maccone says. Only states that avoid paradoxes after the interaction are able to exist beforehand, so the team calls their condition “post-selection.”

To demonstrate these ideas, the team performed an experiment with photons showing that the consistency condition indeed picks out specific states and destroys all the rest. Lacking an actual CTC to perform the post-selection, the team created photons in a specific quantum state for the input, a state where the polarization was not known or measured but had a correlation with another property, associated with the photon’s path. As the photon went through the experiment, it experienced changes that mimicked the 0-to-1 flipping that occurs in the imagined time-travel arrangement. The team found that only those photons that wouldn’t lead to paradoxes made it through unscathed. Although the result is in line with expectation, no one has simulated time travel in this way before.

An odd consequence of post-selection is that because the presence of a CTC annuls paradoxical states completely, it can disallow some states that seem innocuous today but have unacceptable consequences later. “In principle, one could detect the future existence of time machines by … looking for deviations now from the predictions of quantum mechanics,” says Todd Brun of the University of Southern California in Los Angeles. Although, he adds, it’s hard to know in advance what to measure.

–David Lindley

David Lindley is a freelance science writer in Alexandria, Virginia.

• D. Deutsch, “Quantum Mechanics near Closed Timelike Lines,” Phys. Rev. D 44, 3197 (1991)

More Information

Time Travel Beats Quantum Mechanics ( Focus story from 2009)

Closed Timelike Curves via Postselection: Theory and Experimental Test of Consistency

Seth Lloyd, Lorenzo Maccone, Raul Garcia-Patron, Vittorio Giovannetti, Yutaka Shikano, Stefano Pirandola, Lee A. Rozema, Ardavan Darabi, Yasaman Soudagar, Lynden K. Shalm, and Aephraim M. Steinberg

Phys. Rev. Lett. 106 , 040403 (2011)

Published January 27, 2011

Subject Areas

Related articles.

A Simple Electronic Circuit Manifests a Complex Physical Effect

Using a single set of measurements of an electronic circuit, researchers have characterized the properties of the topologically protected edge states of a quantum Hall system. Read More »

Informing Potential Remedies for Quasiparticle Poisoning

Measurements of the temperature distribution of quasiparticles in superconducting circuits reveal behavior that could inform strategies for mitigating quasiparticle-induced errors in superconducting qubits. Read More »

Quantifying Uncertainties in Quantum Simulations

A method for analyzing uncertainties in so-called analog quantum simulations could help scientists make precise predictions using these models. Read More »

Sign up to receive weekly email alerts from Physics Magazine .

Advertisement

Quantum time: Is this where the flow of existence comes from?

Why we perceive the passage of time is one of the biggest mysteries of physics. Now we could have found its source – in our most potent theory of reality

By Michael Brooks

18 April 2018

Henrik Sorensen/Getty

THE philosopher Augustine of Hippo once wrote that he felt he knew what time was, so long as no one asked him. Fast forward 16 centuries and the picture has hardly changed, says physicist Carlo Rovelli . Time is “perhaps the greatest mystery”, he says. “At the most fundamental level we currently know of, there is little that resembles time as we experience it.”

The passage of time – a uniform, universal flow that transports us inexorably from a past we cannot revisit to a future we cannot know – is perhaps the most fundamental experience of our existence. Yet our best theories suggest that it is not real . Time doesn’t flow, and past, present and future cannot sensibly be defined. There isn’t even one single time that governs the order of events.

Rovelli, who works at Aix-Marseille University in France, is just one of many physicists hunting for a better answer. As they do, a new generation of experiments is giving hope that we can probe the nature of time more searchingly than ever before. In all this, a strange realisation is crystallising, one that perhaps brings us a little closer to the heart of the mystery. Maybe we shouldn’t be so worried about our ignorance of time. Perhaps, at some level, time is just that – ignorance.

A century ago, Albert Einstein revolutionised our ideas of time. His theories of relativity gave time a physical identity as part of space-time, a malleable fabric on which reality’s events play out (see “ Why now doesn’t exist, and other strange facts about time ”).

Einstein’s ideas are mathematically sound and rigorously confirmed…

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

To continue reading, subscribe today with our introductory offers

No commitment, cancel anytime*

Offer ends 2nd of July 2024.

*Cancel anytime within 14 days of payment to receive a refund on unserved issues.

Inclusive of applicable taxes (VAT)

Existing subscribers

More from New Scientist

Explore the latest news, articles and features

How materials that rewind light can test physics' most extreme ideas

Subscriber-only

Time may be an illusion created by quantum entanglement

Quantum time travel: the experiment to 'send a particle into the past', quantum 'arrow of time' suggests early universe had no entanglement, popular articles.

Trending New Scientist articles

Time Travel May be Possible Inside the Quantum Realm

Time travel may be possible after all, particularly in the quantum realm. And based on recently published research, this may include moving both backward and forward in time.

BACKGROUND: BUT ISN’T TIME TRAVEL IMPOSSIBLE?

In classical physics, the movement of time is more or less described as a movement from a more organized state to a less organized state. Physicists called this entropy. Such movement can be seen in everyday systems like the rotting of food or the growing of a tree, or the simple process of a meal cooking on the stove. 

Due to this seeming unidirectional aspect to the movement of time, often called time’s arrow, most physicists agree that traveling backwards in time would violate a number of known processes and properties of physics, likely making it all but impossible outside of science fiction .

By comparison, moving forward in time is relatively straightforward. Simply speed up to as close to the speed of light as possible, thereby taking advantage of the relativistic effects that will cause time on the outside world to travel significantly faster than it will for you. In short, if you travel close enough to the speed of light, you will age significantly slower than the world around you, meaning that for all intents and purposes, you will have traveled into the future.

Now, based on new research published in the journal Communications Physics , traveling to the past may be back on the proverbial time travel table.

ANALYSIS: TO TRAVEL BACKWARDS YOU FIRST MUST GO QUANTUM

According to a recent press release ; “a team of physicists from the Universities of Bristol, Vienna, the Balearic Islands and the Institute for Quantum Optics and Quantum Information (IQOQI-Vienna), has shown how quantum systems can simultaneously evolve along two opposite time arrows – both forward and backward in time.”

This unique ability is governed by the quantum principle of superposition, where a single particle of matter can exist in two different states at the same time. According to the researchers behind the latest study, this unique state of matter also allows for the travel of time in both directions, forward and backward.

“We can take the sequence of things we do in our morning routine as an example,” said the study’s lead-author Dr. Giulia Rubino from the University of Bristol’s Quantum Engineering Technology Labs (QET labs). “If we were shown our toothpaste moving from the toothbrush back into its tube, we would be in no doubt it was a re-winded recording of our day. However, if we squeezed the tube gently so only a small part of the toothpaste came out, it would not be so unlikely to observe it re-entering the tube, sucked in by the tube’s decompression.”

“Extending this principle to time’s arrows,” added Rubino, “it results that quantum systems evolving in one or the other temporal direction (the toothpaste coming out of or going back into the tube), can also find themselves evolving simultaneously along both temporal directions.” 

Basically, if this quantum sized hypothetical “toothpaste” can evolve along two different paths as allowed by superposition, then it is possible that one of those paths results in the toothpaste moving back into the tube, essentially going back in time to a previous, less entropic state. According to Rubino, it is precisely this process that his team’s research shows.

“In our work, we quantified the entropy produced by a system evolving in quantum superposition of processes with opposite time arrows,” explained Rubino. “We found this most often results in projecting the system onto a well-defined time’s direction, corresponding to the most likely process of the two.”

In short, most of the time things moved forward in time, just as researchers and classical physics would predict. However, sometimes the opposite happened.

“And yet,” he added, “when small amounts of entropy are involved (for instance, when there is so little toothpaste spilled that one could see it being reabsorbed into the tube), then one can physically observe the consequences of the system having evolved along the forward and backward temporal directions at the same time.”

In conclusion, based on the size and timing of the event, the quantum realm may possess its own equivalent of a five second rule , allowing the movement back in time to a less entropic state in certain circumstances. But what does this mean in the macro world?

OUTLOOK: SO FLUX CAPACITOR OR NO FLUX CAPACITOR?

Like many things that occur in the quantum realm, the findings of this latest research may be counter-intuitive. However, the researchers behind the study say it is a real, actual principle operating inside the quantum world that may have real, macro-world level impacts.

Former President Obama Addresses Controversial Drone Program, Questions About UFOs The 44th President of the United States recently defended the use of drones in military operations while he was in office, and keeps us guessing about UFO briefings.

“Although this idea seems rather nonsensical when applied to our day-to-day experience, at its most fundamental level, the laws of the universe are based on quantum-mechanical principles.”

This revelation also likely means that macro level systems that are affected by processes in the quantum realm, like the ability of birds to sense the Earth’s magnetic field using a quantum mechanical process , may be able to take advantage of these uniquely quantum effects. Apparently, this now includes time travel.

“Although time is often treated as a continuously increasing parameter, our study shows the laws governing its flow in quantum mechanical contexts are much more complex,” said Rubino. ”This may suggest that we need to rethink the way we represent this quantity in all those contexts where quantum laws play a crucial role.”

Okay, somebody call Doc Brown. Anyone seen the keys to my DeLorean?

Follow and connect with author Christopher Plain on Twitter: @plain_fiction  

• Skip to main content
• Keyboard shortcuts for audio player

13.7 Cosmos & Culture

Can we change the past.

Marcelo Gleiser

Who has no regrets about things done in the past? Wouldn't it be nice if, somehow, we could go back to tweak a couple of bad decisions?

This sounds (and as we will see, is, to a certain extent) like science fiction.

The laws of physics prohibit traveling backwards in time for many reasons. If we did travel backwards in time and changed the course of events, we would be altering the course of history. An example often cited is the grandfather's paradox: If you traveled back in time and killed your grandfather when he was still a high school student, he wouldn't have met your grandmother and your father and you wouldn't exist.

A popular example of traveling back in time is the fascinating Canadian TV series Travelers : In a distant future, the Earth is in shambles; humans are controlled by a benevolent artificial intelligence that finds a way to project the consciousness of people into unaware hosts in the 21st century. The idea is that travelers from the future take over the minds of people in the 21st century right before they are about to die. There is some obscure talk about quantum entanglement of consciousness between traveler and host, but this is secondary. The point of the show is that the travelers go back to try to change the course of history — so that the future looks better.

Putting humans or consciousness traveling back in time aside for the moment, is there anything in science even remotely similar? Surprisingly, yes. At the level of quantum particles (we are talking individual photons, elementary particles or individual atoms), there is something called Wheeler's delayed-choice experiments that show that actions in the present can influence the past.

The experiments use something called the wave-particle duality of light and of matter, the fact that the physical nature of quantum objects is undetermined until it is measured. In other words, this means that a particle of light, or of matter, can behave either as a wave (spreading out in space, showing interference) or as a particle (staying together as a small bundle) depending on the measuring apparatus. Long and ongoing discussions about the nature of quantum physics are still trying to work out what this actually means. Do our minds determine the nature of physical reality? The interested reader can see what I wrote about this in more detail in The Island of Knowledge: The Limits of Science and the Search for Meaning .

But experiments measure — they don't ask questions of meaning. John Wheeler , the physicist who proposed such experiments in the 1970s, would have been amazed if he had seen the current results. It does seem that the present can influence the past, at least at the level of quantum objects.

In the double-slit experiment, imagine that the setup — having or not having the screen — is decided after the photon goes through the slits. That is what the arrows in the diagram represent, the possibility that the screen is there — or is not. Courtesy of Marcelo Gleiser hide caption

In the double-slit experiment, imagine that the setup — having or not having the screen — is decided after the photon goes through the slits. That is what the arrows in the diagram represent, the possibility that the screen is there — or is not.

The picture to the right explains the story. Imagine that there is a source of photons (or other small quantum particle). The photons can pass through a double slit. Behind the double slit, there is a screen. If the photons hit the screen, those conducting the experiment observe an interference pattern of bright and dark fringes, typical of waves. If the screen is not there, and there are photon counters aligned with the slits, the photons will hit either one or the other, behaving like little bullets (or particles). So far, this is the typical setup for a double-slit experiment.

The "mystery which cannot go away" (as physicist Richard Feynman famously remarked) of the double-slit experiment, is that the person performing the experiment determines the physical nature of the particle — i.e., whether it is a wave or a particle. And, with Wheeler, the mystery deepens.

Imagine that the setup — having or not having the screen — is decided after the photon goes through the slits. That is what the arrows in the diagram represent, the possibility that the screen is there — or is not. In 2007, a group in France did exactly that , letting a single photon pass through a double slit and then, after it passed through, having a random number generator choose whether the screen would be there or not to detect it. As Wheeler wrote, "Thus one decides the photon shall have come by one route or by both routes after it has already done its travel." Since then, many other groups (for example, here ) have performed refined versions of the experiment, confirming Wheeler's intuition.

An important detail is that the switching over of detecting apparatus must be faster than the time the photon has to travel to the detectors. This way, there is no way the photon could "know" what to do. (If a photon knows anything, anyway.) Experiments presented in October extended the range of the photon's trip to about 2,200 miles, and still the photon seems to always choose the path consistent with the delayed choice. It is as if — Mike McRae wrote in this Science Alert piece — "that even after the horse has bolted 2,200 miles out of the gate, it can still wait until the finish line to decide which race it ran." That is, which path to the finish line it took.

Of course, photons are not people, and to sustain a quantum superposition is very difficult, especially as the size of the object increases. Still, there is something quite amazing and mysterious about this behavior, where the path in space taken by an object seems to be impervious to time; it is as if the two choices (particle or wave; one slit or two) are suspended in time and are only enacted once the spatial arrangement is decided upon. No wonder Wheeler liked to called such ideas as being indicative of a "participatory universe," that is, of a universe where our minds are somehow deeply connected with the very fabric of space and time. After all, the choices of the apparatus may be made by a random number generator, but the apparatus and the interpretation of the data require our intent and design.

Food for thought for the future. Or maybe the past?

Unfortunately, these experiments say very little about how we could interfere with the past in events relevant to the human scale. Better to think carefully about decisions than to try to fix them backwards.

Marcelo Gleiser is a theoretical physicist and writer — and a professor of natural philosophy, physics and astronomy at Dartmouth College. He is the director of the Institute for Cross-Disciplinary Engagement at Dartmouth, co-founder of 13.7 and an active promoter of science to the general public. His latest book is The Simple Beauty of the Unexpected: A Natural Philosopher's Quest for Trout and the Meaning of Everything . You can keep up with Marcelo on Facebook and Twitter: @mgleiser

• time travel
• delayed choice
• quantum particles

• June 6, 2024 | Uncovering the Secret Life of Fungi in Bee Colonies
• June 6, 2024 | Cancer Breakthrough: Scientists Discover Game-Changing New Type of T Cells
• June 6, 2024 | Shocking Findings: High BMI Accelerates Brain Aging by 12 Years
• June 6, 2024 | Lightning Bonds: Capturing Halogen Magic in the Blink of an Eye
• June 6, 2024 | Unlocking Innate Immunity: Key Puzzle Piece Identified

Rewinding Reality: Cambridge Uses Time-Travel Simulations To Solve “Impossible” Problems

By University of Cambridge October 21, 2023

Researchers at the University of Cambridge have utilized quantum entanglement to simulate a scenario resembling backward time travel. This allows for past actions to be retroactively altered, potentially leading to improved present outcomes.

Physicists have shown that simulating models of hypothetical time travel can solve experimental problems that appear impossible to solve using standard physics.

If gamblers, investors, and quantum experimentalists could bend the arrow of time, their advantage would be significantly higher, leading to significantly better outcomes.

“We are not proposing a time travel machine, but rather a deep dive into the fundamentals of quantum mechanics.” — David Arvidsson-Shukur try { window._mNHandle.queue.push(function (){ window._mNDetails.loadTag("974871025", "600x250", "974871025"); }); } catch (error) {}

Researchers at the University of Cambridge have shown that by manipulating entanglement – a feature of quantum theory that causes particles to be intrinsically linked – they can simulate what could happen if one could travel backward in time. So that gamblers, investors and quantum experimentalists could, in some cases, retroactively change their past actions and improve their outcomes in the present.

Simulation and Time Loops

Whether particles can travel backward in time is a controversial topic among physicists, even though scientists have previously simulated models of how such spacetime loops could behave if they did exist. By connecting their new theory to quantum metrology, which uses quantum theory to make highly sensitive measurements, the Cambridge team has shown that entanglement can solve problems that otherwise seem impossible. The study was published on October 12 in the journal Physical Review Letters .

“Imagine that you want to send a gift to someone: you need to send it on day one to make sure it arrives on day three,” said lead author David Arvidsson-Shukur, from the Hitachi Cambridge Laboratory. “However, you only receive that person’s wish list on day two. So, in this chronology-respecting scenario, it’s impossible for you to know in advance what they will want as a gift and to make sure you send the right one.

“Now imagine you can change what you send on day one with the information from the wish list received on day two. Our simulation uses quantum entanglement manipulation to show how you could retroactively change your previous actions to ensure the final outcome is the one you want.”

Understanding Quantum Entanglement

The simulation is based on quantum entanglement, which consists of strong correlations that quantum particles can share and classical particles—those governed by everyday physics—cannot.

The particularity of quantum physics is that if two particles are close enough to each other to interact, they can stay connected even when separated. This is the basis of quantum computing – the harnessing of connected particles to perform computations too complex for classical computers.

“In our proposal, an experimentalist entangles two particles,” said co-author Nicole Yunger Halpern, researcher at the National Institute of Standards and Technology (NIST) and the University of Maryland. “The first particle is then sent to be used in an experiment. Upon gaining new information, the experimentalist manipulates the second particle to effectively alter the first particle’s past state, changing the outcome of the experiment.”

“The effect is remarkable, but it happens only one time out of four!” said Arvidsson-Shukur. “In other words, the simulation has a 75% chance of failure. But the good news is that you know if you have failed. If we stay with our gift analogy, one out of four times, the gift will be the desired one (for example a pair of trousers), another time it will be a pair of trousers but in the wrong size, or the wrong color, or it will be a jacket.”

Practical Applications and Limitations

To give their model relevance to technologies, the theorists connected it to quantum metrology. In a common quantum metrology experiment, photons—small particles of light—are shone onto a sample of interest and then registered with a special type of camera. If this experiment is to be efficient, the photons must be prepared in a certain way before they reach the sample. The researchers have shown that even if they learn how to best prepare the photons only after the photons have reached the sample, they can use simulations of time travel to retroactively change the original photons.

To counteract the high chance of failure, the theorists propose to send a huge number of entangled photons, knowing that some will eventually carry the correct, updated information. Then they would use a filter to ensure that the right photons pass to the camera, while the filter rejects the rest of the ‘bad’ photons.

“Consider our earlier analogy about gifts,” said co-author Aidan McConnell, who carried out this research during his master’s degree at the Cavendish Laboratory in Cambridge, and is now a PhD student at ETH, Zürich. “Let’s say sending gifts is inexpensive and we can send numerous parcels on day one. On day two we know which gift we should have sent. By the time the parcels arrive on day three, one out of every four gifts will be correct, and we select these by telling the recipient which deliveries to throw away.”

“That we need to use a filter to make our experiment work is actually pretty reassuring,” said Arvidsson-Shukur. “The world would be very strange if our time-travel simulation worked every time. Relativity and all the theories that we are building our understanding of our universe on would be out of the window.

“We are not proposing a time travel machine, but rather a deep dive into the fundamentals of quantum mechanics. These simulations do not allow you to go back and alter your past, but they do allow you to create a better tomorrow by fixing yesterday’s problems today.”

Reference: “Nonclassical Advantage in Metrology Established via Quantum Simulations of Hypothetical Closed Timelike Curves” by David R. M. Arvidsson-Shukur, Aidan G. McConnell and Nicole Yunger Halpern, 12 October 2023, Physical Review Letters . DOI: 10.1103/PhysRevLett.131.150202

This work was supported by the Sweden-America Foundation, the Lars Hierta Memorial Foundation, Girton College, and the Engineering and Physical Sciences Research Council (EPSRC), part of UK Research and Innovation (UKRI).

More on SciTechDaily

Gamma Factory: New ‘Super Light Source’ at CERN for Fascinating Insights Into Atoms

Ancient DNA Analysis Reveals Large Scale Migrations Into Bronze Age Britain

Conventional Computers Can Learn To Solve Tricky Quantum Problems in Physics and Chemistry

Electrons Waiting Their Turn: New Model Explains 3D Quantum Material

Arctic Melt Season Is Lengthening by Several Days Each Decade

Study Shows Star RZ Piscium May Be Devouring Wrecked Planets

MIT’s New Fluxonium Qubit Circuit Enables Quantum Operations With Unprecedented Accuracy

Concerning – Popular Hawaiian Tourist Spot Is Being “Overused”

5 comments on "rewinding reality: cambridge uses time-travel simulations to solve “impossible” problems".

So how do we fast track a path to getting the correct answer 4 out of 4 times so that we aren’t at a 25% correct answer ? That’s my question

not provable, I won’t get in to explaining other than given a persons preferences and a multiple amount of life scenarios of such person and prier choices made a list can be formulated with high to low preferences. There are something that simply cannot be changed that’s history and time is fleeting we make it what it is.

Weren’t we just here about a week ago with a similar scenario and that article mysteriously disappeared into some sort of blackhole shortly after it was published? Since the very basis of the worthiness of capitalism is to gain at the expense of others, I can definitely see its value. Of course the experiment could be run in the future with no problem whatsoever and if the answer should be wrong, it could be run again until the correct answer is achieved, then wait, for time to catch up to the tested event, that way if it were to turn out that time is by nature non-euclidean, even a filter would still produce unacceptable errors, such as what occurs in the high energy fields needed for particle accelerators where virtual particles interfer with the desired observation. Something like that, if we think of time in the same manner as we do space, because other research has already revealed that reality.

Surely this is the equivalent of trying to use entanglement to send information faster than light which is forbidden. The proposed filter must fail.

The gifts analogy is flawed. If I send four gifts one day one, on day two I find out the correct one, and day three I tell him to filter out the three incorrect gifts this is not time travel, simulated or otherwise

Leave a comment Cancel reply

Email address is optional. If provided, your email will not be published or shared.

Save my name, email, and website in this browser for the next time I comment.

Is Time Travel Possible?

We all travel in time! We travel one year in time between birthdays, for example. And we are all traveling in time at approximately the same speed: 1 second per second.

We typically experience time at one second per second. Credit: NASA/JPL-Caltech

NASA's space telescopes also give us a way to look back in time. Telescopes help us see stars and galaxies that are very far away . It takes a long time for the light from faraway galaxies to reach us. So, when we look into the sky with a telescope, we are seeing what those stars and galaxies looked like a very long time ago.

However, when we think of the phrase "time travel," we are usually thinking of traveling faster than 1 second per second. That kind of time travel sounds like something you'd only see in movies or science fiction books. Could it be real? Science says yes!

This image from the Hubble Space Telescope shows galaxies that are very far away as they existed a very long time ago. Credit: NASA, ESA and R. Thompson (Univ. Arizona)

How do we know that time travel is possible?

More than 100 years ago, a famous scientist named Albert Einstein came up with an idea about how time works. He called it relativity. This theory says that time and space are linked together. Einstein also said our universe has a speed limit: nothing can travel faster than the speed of light (186,000 miles per second).

Einstein's theory of relativity says that space and time are linked together. Credit: NASA/JPL-Caltech

What does this mean for time travel? Well, according to this theory, the faster you travel, the slower you experience time. Scientists have done some experiments to show that this is true.

For example, there was an experiment that used two clocks set to the exact same time. One clock stayed on Earth, while the other flew in an airplane (going in the same direction Earth rotates).

After the airplane flew around the world, scientists compared the two clocks. The clock on the fast-moving airplane was slightly behind the clock on the ground. So, the clock on the airplane was traveling slightly slower in time than 1 second per second.

Credit: NASA/JPL-Caltech

Can we use time travel in everyday life?

We can't use a time machine to travel hundreds of years into the past or future. That kind of time travel only happens in books and movies. But the math of time travel does affect the things we use every day.

For example, we use GPS satellites to help us figure out how to get to new places. (Check out our video about how GPS satellites work .) NASA scientists also use a high-accuracy version of GPS to keep track of where satellites are in space. But did you know that GPS relies on time-travel calculations to help you get around town?

GPS satellites orbit around Earth very quickly at about 8,700 miles (14,000 kilometers) per hour. This slows down GPS satellite clocks by a small fraction of a second (similar to the airplane example above).

GPS satellites orbit around Earth at about 8,700 miles (14,000 kilometers) per hour. Credit: GPS.gov

However, the satellites are also orbiting Earth about 12,550 miles (20,200 km) above the surface. This actually speeds up GPS satellite clocks by a slighter larger fraction of a second.

Here's how: Einstein's theory also says that gravity curves space and time, causing the passage of time to slow down. High up where the satellites orbit, Earth's gravity is much weaker. This causes the clocks on GPS satellites to run faster than clocks on the ground.

The combined result is that the clocks on GPS satellites experience time at a rate slightly faster than 1 second per second. Luckily, scientists can use math to correct these differences in time.

If scientists didn't correct the GPS clocks, there would be big problems. GPS satellites wouldn't be able to correctly calculate their position or yours. The errors would add up to a few miles each day, which is a big deal. GPS maps might think your home is nowhere near where it actually is!

In Summary:

Yes, time travel is indeed a real thing. But it's not quite what you've probably seen in the movies. Under certain conditions, it is possible to experience time passing at a different rate than 1 second per second. And there are important reasons why we need to understand this real-world form of time travel.

If you liked this, you may like:

October 21, 2021

10 min read

Can We Gauge Quantum Time of Flight?

Measuring the time it takes particles to travel between two points may be the best test yet for Bohmian mechanics

By Anil Ananthaswamy

Kenn Brown, Mondolithic Studios

A deceptively simple experiment that involves making precise measurements of the time it takes for a particle to go from point A to point B could cause a breakthrough in quantum physics. The findings could focus attention on an alternative to standard quantum theory called Bohmian mechanics, which posits an underworld of unseen waves that guide particles from place to place.

A new study, by a team at the Ludwig Maximilian University of Munich (L.M.U.) in Germany, makes precise predictions for such an experiment using Bohmian mechanics, a theory formulated by theoretical physicist David Bohm in the 1950s and augmented by modern-day theorists. Standard quantum theory fails in this regard, and physicists have to resort to assumptions and approximations to calculate particle transit times. “If people knew that a theory that they love so much—standard quantum mechanics—cannot make [precise] predictions in such a simple case, that should at least make them wonder,” says theorist and L.M.U. team member Serj Aristarhov.

It is no secret that the quantum world is weird. Consider a setup in which an electron gun fires the subatomic particles at a screen, as in the classic “double-slit experiment” [ see graphic below ]. You cannot predict exactly where any given electron will land to form, say, a fluorescent dot. But you can predict with precision the spatial distribution, or pattern, of dots that takes shape over time as the electrons land one by one. Some locations will have more electrons; others will have fewer. But this weirdness hides something even stranger. All else being equal, each electron will reach the detector at a slightly different time, its so-called arrival time. Just like the positions, the arrival times will have a distribution: some arrival times will be more common, and others will be less so. Textbook quantum physics has no mechanism for precisely predicting this temporal distribution. “Normal quantum theory is concerned only with ‘where’; they ignore the ‘when,’” says team member and theorist Siddhant Das. “That’s one way to diagnose that there’s something fishy.”

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

There is a deep reason for this curious shortcoming. In standard quantum theory, a physical property that can be measured is called an observable. The position of a particle, for example, is an observable. Each and every observable is associated with a corresponding mathematical entity called an operator. But the standard theory has no such operator for observing time. In 1933 Austrian theoretical physicist Wolfgang Pauli showed that quantum theory could not accommodate a time operator, at least not in the standard way of thinking about it. “We conclude therefore that the introduction of a time operator ... must be abandoned fundamentally,” he wrote.

Yet measuring particle arrival times, or their “time of flight,” is an important part of experimental physics. Detectors at CERN’s Large Hadron Collider, for example, and instruments called mass spectrometers use such measurements to calculate the masses and momenta of particles, ions and molecules. There is, however, a serious wrinkle: although these calculations concern quantum systems, they cannot be made using unadulterated quantum mechanics. Instead they require assumptions. In one method, for example, experimenters assume that once the particle leaves its source, it behaves classically, meaning it follows Newton’s equations of motion.

The result is a hybrid approach—one that is part quantum, part classical. It starts with the quantum perspective, in which each particle is represented by a mathematical abstraction called a wave function. Identically prepared particles will have identical wave functions when they are released from their source. But measuring the momentum of each particle (or, for that matter, its position) at the instant of release will yield different values each time. Taken together, these values follow a distribution that is precisely predicted by the initial wave function. Starting from this ensemble of values for identically prepared particles and assuming that a particle follows a classical trajectory once it is emitted, the result is a distribution of arrival times at the detector that depends on the initial momentum distribution.

Standard theory is also often used for another quantum-mechanical method for calculating arrival times. As a particle flies toward a detector, its wave function evolves according to the Schrödinger equation, which describes a particle’s changing state over time. Consider the one-dimensional case of a detector that is a certain horizontal distance from an emission source. The Schrödinger equation determines the wave function of the particle—and hence the probability of detecting that particle at that location—assuming that the particle crosses the location only once. (There is, of course, no clear way to substantiate this assumption in standard quantum mechanics.) Using such assumptions, physicists can calculate the probability that the particle will arrive at the detector at a given time ( t ) or earlier. “From the perspective of standard quantum mechanics, it sounds perfectly fine,” Aristarhov says. “And you expect to have a nice answer from that.”

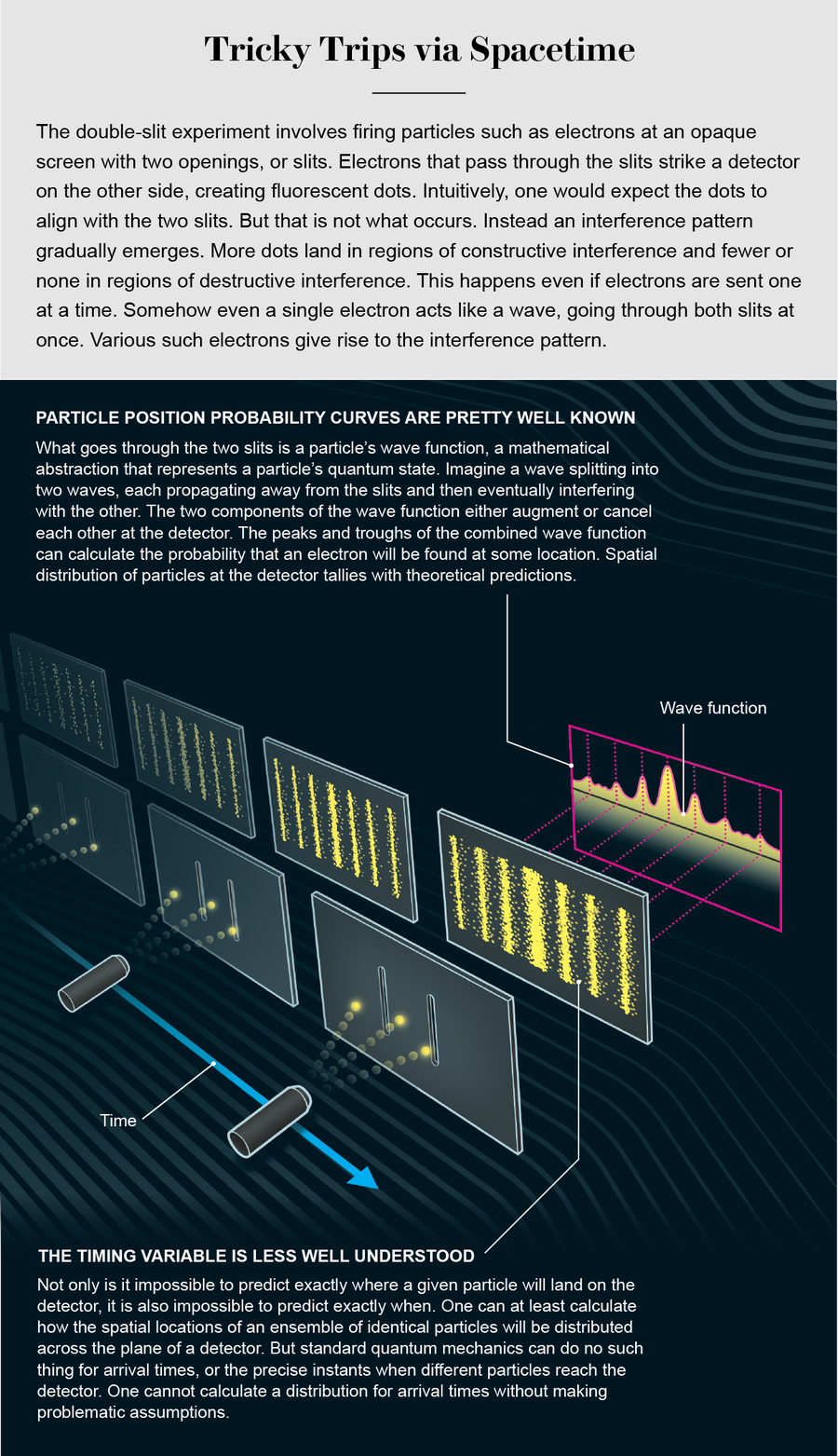
Credit: Nick Bockelman

There is a hitch, however. To go from the probability that the arrival time is less than or equal to t to the probability that it is exactly equal to t involves calculating a quantity that physicists call the quantum flux, or quantum probability current—a measure of how the probability of finding the particle at the detector location changes with time. This works well, except that at times the quantum flux can be negative. Even though it is hard to find wave functions for which the quantity becomes appreciably negative, nothing “prohibits this quantity from being negative,” Aristarhov says. “And this is a disaster.” A negative quantum flux leads to negative probabilities, and probabilities can never be less than zero.

Using the Schrödinger evolution to calculate the distribution of arrival times works only when the quantum flux is positive—a case that, in the real world, only definitively exists when the detector is in the “far field,” or at a considerable distance from the source, and the particle is moving freely in the absence of potentials. When experimentalists measure such far-field arrival times, both the hybrid and quantum-flux approaches make similar predictions that tally well with experimental findings. But they do not make clear predictions for “near field” cases, where the detector is very close to the source.

Bohmian Predictions

In 2018 Das and Aristarhov, along with their then Ph.D. adviser Detlef Dürr, an expert on Bohmian mechanics at L.M.U., who died in 2021, began working with colleagues on Bohmian-based predictions of arrival times. Bohm’s theory holds that each particle is guided by its wave function. Unlike standard quantum mechanics, in which a particle is considered to have no precise position or momentum prior to a measurement—and hence no trajectory—particles in Bohmian mechanics are real and have squiggly trajectories described by precise equations of motion (albeit ones that differ from Newton’s equations of motion).

Among the researchers’ first findings was that far-field measurements would fail to distinguish between the predictions of Bohmian mechanics and those of the hybrid or quantum-flux approaches. This is because over large distances Bohmian trajectories become straight lines, so the hybrid semiclassical approximation holds. Also, for straight far-field trajectories, the quantum flux is always positive, and its value is predicted exactly by Bohmian mechanics. “If you put a detector far enough [away] and you do Bohmian analysis, you see that it coincides with the hybrid approach and the quantum-flux approach,” Aristarhov says.

The key, then, is to do near-field measurements—but those have long been considered impossible. “The near-field regime is very volatile,” Das says. “It’s very sensitive to the initial wave-function shape you have created.” Also, “if you come very close to the region of initial preparation, the particle will just be detected instantaneously. You cannot resolve [the arrival times] and see the differences between this prediction and that prediction.”

To avoid this problem, Das and Dürr proposed an experimental setup that would allow particles to be detected far away from the source while still generating unique results that could distinguish the predictions of Bohmian mechanics from those of the more standard methods.

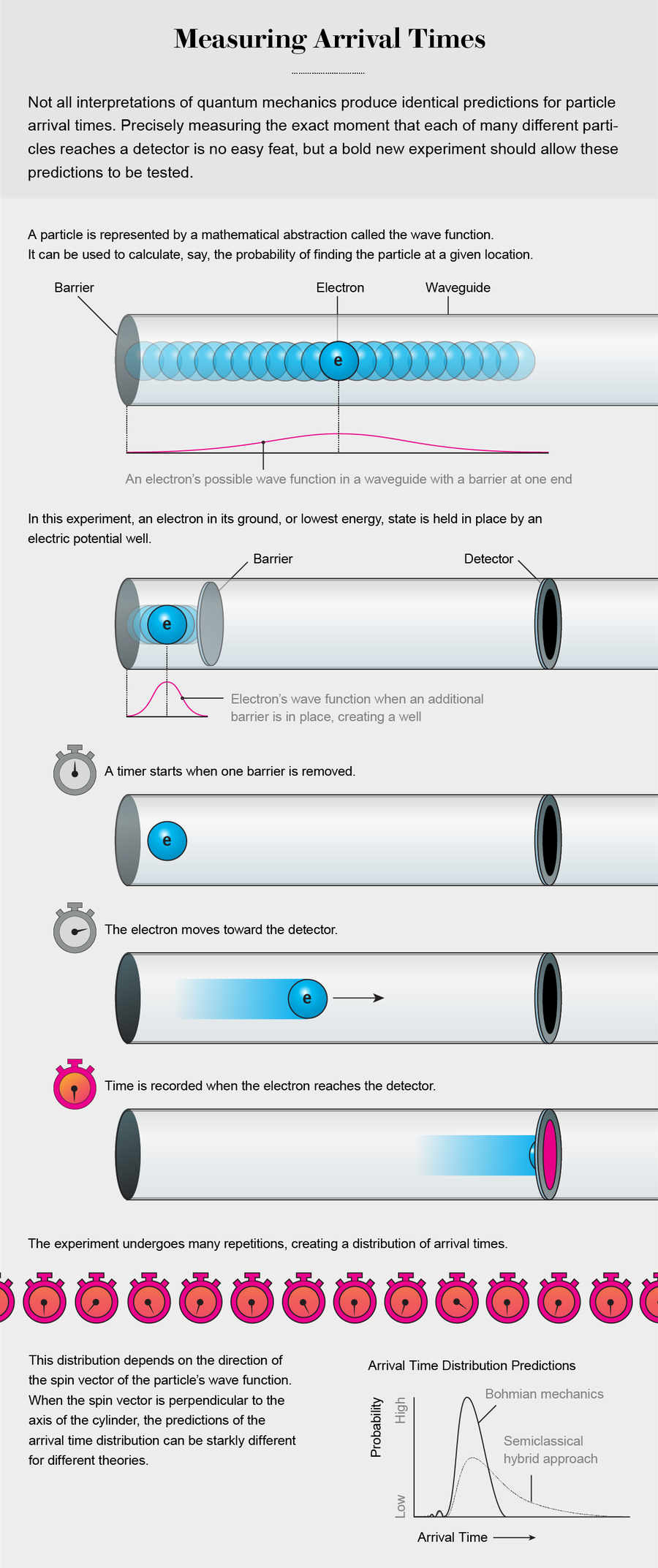
Credit: Jen Christiansen

Conceptually, the team’s proposed setup is simple. Imagine a waveguide—a cylindrical pathway that confines the motion of a particle (an optical fiber is such a waveguide for photons of light, for example). On one end of the waveguide, prepare a particle—ideally an electron or some particle of matter—in its lowest energy, or ground, state and trap it in a bowl-shaped electric potential well. This well is actually the composite of two adjacent potential barriers that collectively create the parabolic shape. If one of the barriers is switched off, the particle will still be blocked by the other that remains in place, but it is free to escape from the well into the waveguide.

Das pursued the painstaking task of fleshing out the experiment’s parameters, performing calculations and simulations to determine the theoretical distribution of arrival times at a detector placed far away from a source along a waveguide’s axis. After a few years of work, he had obtained clear results for two different types of initial wave functions associated with particles such as electrons. Each wave function can be characterized by something called its spin vector. Imagine an arrow associated with the wave function that can be pointing in any direction. The team looked at two cases: one in which the arrow points along the axis of the waveguide and another in which it is perpendicular to that axis.

The team showed that when the wave function’s spin vector is aligned along the waveguide’s axis, the distribution of arrival times predicted by the quantum-flux method is identical to that predicted by Bohmian mechanics. But these distributions differ significantly from those calculated for the hybrid approach. When the spin vector is perpendicular, the distinctions become even starker. With help from their L.M.U. colleague Markus Nöth, the researchers showed that all the Bohmian trajectories will strike the detector at or before this cutoff time. “This was very unexpected,” Das says.

Again, the Bohmian prediction differs significantly from the predictions of the semiclassical hybrid theory, which do not exhibit such a sharp arrival-time cutoff. And crucially, in this scenario, the quantum flux is negative, meaning that calculating arrival times using Schrödinger evolution becomes impossible. The standard quantum theorists “put their hands up when [the quantum flux] becomes negative,” Das says. But Bohmian mechanics continues to make predictions. “There’s a clear distinction between [it] and everything else,” Aristarhov says.

Experimentalists Enter the Fray

Quantum theorist Charis Anastopoulos of the University of Patras in Greece, an expert on arrival times, who was not involved with this work, is both impressed and circumspect. “The setup they are proposing seems plausible,” he says. And because each approach to calculating the distribution of arrival times involves a different way of thinking about quantum reality, a clear experimental finding could jolt the foundations of quantum mechanics. “It will vindicate particular ways of thinking,” Anastopoulos says. “So in this way, it will have some impact.... If it [agrees with] Bohmian mechanics, which is a very distinctive prediction, this would be a great impact, of course.”

At least one experimentalist is gearing up to make the team’s proposal a reality. Before Dürr’s death, Ferdinand Schmidt-Kaler of the Johannes Gutenberg University Mainz in Germany had been in discussions with him about testing arrival times. Schmidt-Kaler is an expert on a type of ion trap in which electric fields are used to confine a single calcium ion. An array of lasers is used to cool the ion to its quantum ground state, where the momentum and position uncertainties of the ion are at their minimum. The trap is a three-dimensional bowl-shaped region created by the combination of two electric potentials; the ion sits at the bottom of this “harmonic” potential. Switching off one of the potentials creates conditions similar to what is required by the theoretical proposal: a barrier on one side and a sloping electric potential on the other side. The ion moves down that slope, accelerates and gains velocity. “You can have a detector outside the trap and measure the arrival time,” Schmidt-Kaler says. “That is what made it so attractive.”

For now his group has done experiments in which the researchers eject the ion out of its trap and detect it outside. They showed that the time of flight is dependent on a particle’s initial wave function. The results were published in 2021 in the New Journal of Physics . Schmidt-Kaler and his colleagues have also performed not yet published tests of the ion exiting the trap only to be reflected back in by an “electric mirror” and recaptured—a process the setup achieves with 98 percent efficiency, he says. “We are underway,” Schmidt-Kaler says. “Of course, it is not tuned to optimize this measurement of the time-of-flight distribution, but it could be.”

That is easier said than done. The detector outside the ion trap will likely be a sheet of laser light, and the team will have to measure the ion’s interaction with the light sheet to nanosecond precision. The experimentalists will also need to switch off one half of the harmonic potential with similar temporal precision—another serious challenge. These and other pitfalls abound on the path between theoretical prediction and experimental realization.

Still, Schmidt-Kaler is excited about the prospect of using time-of-flight measurements to test the foundations of quantum mechanics. “This has the attraction of being completely different from other [kinds of] tests. It really is something new,” he says. “This will go through many iterations. We will see the first results, I hope, in the next year. That’s my clear expectation.” Meanwhile Aristarhov and Das are reaching out to others, too. “We really hope that the experimentalists around the world notice our work,” Aristarhov says. “We will join forces to do the experiments.”

In a yet to be published paper co-authored by Dürr before he died, the closing words could almost be an epitaph: “It should be clear by now that the chapter on time measurements in quantum physics can only be written if genuine quantum-mechanical time-of-flight data become available.” Which theory will the experimental data pick out as correct—if any? As Dürr wrote, “It’s a very exciting question.”

Watch This Next

Anil Ananthaswamy is author of The Edge of Physics (Houghton Mifflin Harcourt, 2010), The Man Who Wasn't There (Dutton, 2015), Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality (Dutton, 2018), and Why Machines Learn: The Elegant Math Behind AI (Dutton, 2024).

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• News & Views
• Published: 03 June 2024

Topological antiferromagnet

Electronic transport goes quantum at room temperature

• Su-Yang Xu   ORCID: orcid.org/0000-0002-9808-6572 1  

Nature Physics ( 2024 ) Cite this article

955 Accesses

2 Altmetric

Metrics details

• Spintronics
• Topological insulators

In solids, the quantum metric captures the quantum coherence of the electron wavefunctions. Recent experiments demonstrate the detection and manipulation of the quantum metric in a noncollinear topological antiferromagnet at room temperature.

This is a preview of subscription content, access via your institution

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 12 print issues and online access

195,33 € per year

only 16,28 € per issue

Buy this article

• Purchase on Springer Link
• Instant access to full article PDF

Prices may be subject to local taxes which are calculated during checkout

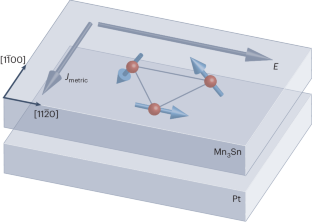
Han, J. et al. Nat. Phys. https://doi.org/10.1038/s41567-024-02476-2 (2024).

Article   Google Scholar  

Orenstein, J. et al. Annu. Rev. Condens. Matter Phys. 12 , 247–272 (2021).

Article   ADS   Google Scholar  

Tokura, Y. & Nagaosa, N. Nat. Commun. 9 , 3740 (2018).

Ma, Q., Grushin, A. G. & Burch, K. S. Nat. Mater. 20 , 1601–1614 (2021).

Tan, H. et al. Nature 614 , 440–444 (2023).

Gao, Y., Yang, S. A. & Niu, Q. Phys. Rev. Lett. 112 , 166601 (2014).

Gao, A. et al. Science 381 , 181–186 (2023).

Wang, N. et al. Nature 621 , 487–492 (2023).

Yin, J.-X., Lian, B. & Hasan, M. Z. Nature 612 , 647–657 (2022).

Download references

Author information

Authors and affiliations.

Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA, USA

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Su-Yang Xu .

Ethics declarations

Competing interests.

The author declares no competing interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Xu, SY. Electronic transport goes quantum at room temperature. Nat. Phys. (2024). https://doi.org/10.1038/s41567-024-02527-8

Download citation

Published : 03 June 2024

DOI : https://doi.org/10.1038/s41567-024-02527-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Higher Perspectives

Scientists Successfully Sent A Particle Back in Time, Is Human Time Travel Next?

Posted: May 30, 2024 | Last updated: May 31, 2024

This article may contain affiliate links .

While the concept of time is something that we as humans made up to make life easier. What even is time? Time is important in our daily lives now, but at one point we lived by the sunrise and sunset.

Science tries to help us make sense of our world and attempts to understand how much we control, and how much happens around us. New discoveries can defy the laws of physics that we have relied on so far. Recently, the way we conceptualize time has been put into question. Scientists have just supported that theoretically, time travel is possible. Here's what that means for the world as we know it. Continue reading to learn more!

Click HERE to learn what Numerology says about your life using only your Birth Date.

Fictional Knowledge Of Time Travel

Up till very recently, time travel was nothing but a concept of science fiction, meant to activate our imagination and entertain us.

The idea of time travel dates back to the 1800s when Wells published The Time Machine , a story about an inventor who builds a device that travels through a fourth, temporal dimension.

Not Just Fantasy

But what if time travel didn't just exist in the world of fantasy? This is a question that scientists try to answer at the risk of attempting to unlock a phenomenon not meant for our species. If the movies were right the price to pay could be lethal if we really do manage to figure out how to travel in time.

For all, we know we could rewrite our whole story. You and I might never exist. Before we jump the gun here's what we know so far. Are you interested in learning more about the secrets of your universe? Tap into the 4,000-year-old science of Numerological Analysis with a FREE Numerology video report!

Time Is A Made Up Concept

Thanks to some history-making scientists, we've made strides in our understanding of the universe and the makings of time. For instance, Einstein's equations brought us into the quantum realm and a more nuanced view of time.

But mathematical logician Kurt Gödel took it one step further and worked out that Einstein’s equations allowed for time travel into the past.

Scientists Took The Challenge

The problem was there was still no found method that was compatible with our physical grounds. The answer to that was: "Why stick to physical grounds?" This was the question that inspired scientists from the Argonne National Laboratory, the Moscow Institute of Physics and Technology, and ETH Zurich.

This was how they successfully sent a particle back in time.

No Past, Present Or Future

Because of the laws of gravity and physics in general that we've imposed and taught in school, we consider time as linear with no way to access the past and no way of fast-forwarding into the future.

However, this isn't an always agreed-upon statement.

It's Not That Simple

There are laws of physics that don't distinguish the future from the past and say that they all operate at the same time.

This goes against the second law of thermodynamics, which states that a closed system always moves from order to disorder. If that didn't make sense, it's basically saying that once you fry an egg, you can't revert it back to the closed initial egg.

Time Moving Linearly

Because of that second law of thermodynamics, we assumed that time was linear and always moving forward. We called this the arrow of time.

This means that once you crack an egg, it's irreversible.

Rules Were Made To Be Broken

Like an arrow released, time moves in a single direction, and we witness the effect as time.

That's why our human-made system of understanding time as moving forward works. But some laws are meant to be broken...Could this one be one of them?

Testing Time Itself

We trapped ourselves by the second law of thermodynamics. It made sense for the way that we experienced the world. However, it didn't answer all of our questions.

That's why an international team of scientists wanted to see if the second law could be broken in the quantum realm.

Powerful Computers

Keep in mind that quantum computers don't work as simply as the computer you're reading this on. While traditional computers work with a binary system of 1 or 0, a quantum computer uses a basic unit of information called a qubit where both 1 and 0 exist simultaneously. This helps it process information much faster.

In their experiment, the researchers substituted qubits for particles.

The Quantum Process

If you're interested in the details, the first step involved making sure the qubits were ordered, so that whatever happens to one, affects all the others too. Second, they launched an evolution program on the quantum computer, which used microwave radio pulses to break down that initial order into a more complex state.

Pushing Back

The third step moves them again, this time rewinding the particulates to their past, orderly selves. In simpler terms, this is the equivalent of pushing against the ripples of a pond to return them to their source, according to study author Valerii M. Vinokur.

We Jumped Through Time!

Quantum mechanics is about probability so nothing in it is ever guaranteed. Still however, the algorithm managed a time jump 85 percent of the time. That's considerable consistency!

However every time they tried to increase the number of qubits to three, the success rate dropped to about 50 percent. The researchers published their results in Scientific Reports .

Human Time Travel Isn't Happening Any Time Soon

Unfortunately despite this leap in science, we can't all just jump in a time machine just yet. This experiment shows us that sending a particle back in time is possible but that it takes an incredible amount of work and outside manipulation. Considering that humans hold around 7,000,000,000,000,000,000,000,000,000 (7 octillion) atoms or particles, there is still a lot of room for advancement with this research.

"We demonstrate that time-reversing even ONE quantum particle is an unsurmountable task for nature alone," study author Vinokur wrote . “The system comprising two particles is even more irreversible, let alone the eggs — comprising billions of particles — we break to prepare an omelet.”

The Secrets Of The Universe

As of now everything is still up in the air. Whether we will make it to a point where we can time travel is possible but unlikely, at least not in our lifetime.

According to a press release: the "timeline required for [an external force] to spontaneously appear and properly manipulate the quantum waves" to appear in nature and unscramble an egg would extend longer than that of the universe itself.”

Anything Is Possible

Research and experiments are how we move forward. We've accomplished things other generations couldn't have even dreamed so who knows just how much further we could go. "Our algorithm could be updated and used to test programs written for quantum computers and eliminate noise and errors," says study author Andrey Lebedev.

Many Possibilities

After all Time travel could also be possible if you traveled around two colliding cosmic strings, traveled through a spinning black hole, or stretched space via negative matter. So the options are endless!

The Numerology of your birth date, regardless of your Zodiac sign, can help you discover detailed information about who you truly are and what is hiding in your subconscious. You won't believe how accurate it is!

Sign up for our newsletter here!

More for You

Donald Trump Wants Five Lawmakers Indicted

Wonder Woman's Lynda Carter, 72, wows in silver swimsuit to promote new music

17 Phrases Confident People Use When They Want to Be Assertive But Not Rude

Lame-Duck Mike: 'No One Wants' It, Admits Cowboys' McCarthy

Insurance companies are monitoring homes from the sky, causing headache for some homeowners

The Only Ingredients Bobby Flay Uses To Season His Burgers

Drinking Water Recall: Full List of Companies With Ongoing Warnings

What Causes Motorcycle Death Wobble, And How Can You Fix It?

Naruto Shippuden's Best Filler, Ranked

Patricia Heaton Joins ‘Frasier', Reuniting With Kelsey Grammer

Caitlin Clark is "Not Built" For The WNBA, Says Geno Auriemma

We gave our daughter $20,000 for a wedding, but she used it for a home down payment and paid for her own wedding. Everyone was happy.

This Beer Battered Fish Is Light, Flaky, and Crispy Golden

5 Bad Habits To Avoid For Extending The Life Of Your Car's CVT Transmission

Keep Annoying Flies Out Of Your Home With Two Kitchen Ingredients

'NCIS': 14 Things You Didn't Know About The Show

What Polls Show About Donald Trump vs. Joe Biden 1 Week After NY Conviction

10 most common PINs have been revealed – see if yours is on the list

What’s the world’s tallest mountain? Here's why some feel the title should be reconsidered

Putin Rages As Reporter Asks About Attacking Nato: 'Are You As Dumb As This Table?'

• How Two Rebel Physicists Changed Quantum Theory

David Bohm and Hugh Everett were once ostracized for challenging the dominant thinking in physics. Now, science accepts their ideas, which are said to enrich our understanding of the universe.

The field of quantum mechanics dates to 1900, the year German scientist Max Planck (1858–1947) discovered that energy could come in discrete packages called quanta. It advanced in 1913, when Danish physicist Niels Bohr (1885–1962) used quantum principles to explain what had until then been inexplicable, the exact wavelengths of light emitted or absorbed by a gas of hydrogen atoms. And since the 1920s, when Werner Heisenberg (1901–1976) and Erwin Schrödinger (1887–1961) built new quantum theories, quantum mechanics has consistently proven its value as the fundamental theory of the nanoscale and as a source of technology, from computer chips and lasers to LED bulbs and solar panels.

One question, however, still puzzles: how does the quantum world relate to the more familiar human-scale one? For a century, the Copenhagen interpretation , chiefly developed by Bohr and Heisenberg in that city, has been the standard answer taught in physics courses. It posits that the quantum scale is indeterminate; that is, operates according to the laws of probability. This world is utterly different from the deterministic and predictable “classical” human scale, yet the Copenhagen interpretation doesn’t clearly explain how reality changes between the two worlds.

Heisenberg and Bohr developed the Copenhagen interpretation amidst the blossoming of new quantum theories in the first half of the twentieth century. In 1927, Heisenberg announced his important uncertainty principle : at the quantum level, certain pairs of quantities, such as momentum and position, cannot be simultaneously measured to any desired degree of precision. The more exactly you measure one, the less well you know the other. Thus, we can never fully know the quantum world, a key feature of the Copenhagen interpretation.

Indeterminism also appears in the Schrödinger wave equation at the heart of the Copenhagen view. Einstein had shown that light waves can act like swarms of particles, later called photons; in 1924, Louis de Broglie assumed the inverse, that tiny particles are also wave-like. In 1926, Schrödinger published his equation for these “matter waves.” Its solution, the “wave function” denoted by the Greek letter Ψ (psi), contains all possible information about a quantum entity such as an electron in an atom. But the information is indeterminate: Ψ is only a list of probable values for all the different physical properties, such as position or momentum, that the electron could have in its particular surroundings. The electron is said be in a superposition , simultaneously present in all its potential states of actual being.

This superposition exists until an observer measures the properties of the electron, which makes its wave function “collapse”; the cloud of possible outcomes yields just one result, a definite value emerging into the classical world. It is as if, asked to pick a card out of a deck, the instant you select the three of hearts, the other fifty-one cards fade away. In this case, we know that the rejected cards still physically exist with definite properties, but in the Copenhagen view, subatomic particles aren’t real until they’re observed. Another problem is that the notion of a sudden wave function collapse seems an arbitrary addition to the Copenhagen interpretation; it contradicts the smooth evolution in time built into the Schrödinger equation.

These troubling features, called “the measurement problem,” were hotly debated in the 1920s. But overwhelming any objections was the fact that the Copenhagen interpretation works! Its results agree precisely with experiments, the final test of any theory, and inspire real devices. Even so, David Joseph Bohm (1917–1992) and Hugh Everett III (1930–1982) sought equally valid theories without any incongruities. In the 1950s, these two American physicists dared to challenge the conventional Copenhagen interpretation with their “pilot wave” and “many-worlds” theories, respectively. Though from different backgrounds, Bohm and Everett shared characteristics that helped them seek answers: mathematical aptitude, necessary to manipulate quantum theory; and unconventional career paths, which separated them from the orthodoxy of academic physics.

Bohm was a second-generation American, born into an immigrant family from Europe that operated a furniture store in Wilkes-Barre, Pennsylvania. In high school, where his physics instructor described him as “outstanding” and “brilliant,” Bohm developed his own alternative ideas about Bohr’s hydrogen atom. After undergraduate work at Penn State, he began earning a PhD in nuclear physics in 1941 under J. Robert Oppenheimer (1904–1967) at the University of California, Berkeley. The United States was engaged in World War II at the time and was about to build an atomic bomb. Bohm’s doctoral research was classified, and he was awarded his degree in 1943 without writing a dissertation. Though Oppenheimer wanted Bohm to work with him at Los Alamos, Bohm couldn’t get security clearance as he had briefly been, in the early 1940s, a member of the Communist Party.

In 1947, supported by theorist John Wheeler, Bohm became an assistant professor at Princeton. There he taught quantum mechanics and wrote Quantum Theory (1951), in which he presented the Copenhagen interpretation, only to disavow it the next year, when he published his alternative theory in a pair of papers in the Physical Review (in 1957, he expounded his ideas further in his book Causality and Chance in Modern Physics ).

But in 1951, his life had taken a serious turn. In that Cold War era of McCarthyism, Bohm was brought before the House Committee on Un-American Activities (HUAC). He pleaded the Fifth Amendment against self-incrimination, and he was first indicted and jailed for contempt of Congress and then acquitted when the Supreme Court decriminalized this action. Still, the damage was done. Princeton didn’t renew Bohm’s contract and banned him from campus in June 1951. Unable to obtain a new academic position in the US, he began a life-long exile, taking temporary teaching positions in Brazil and elsewhere. Finally, in 1961, he accepted the offer of a chaired professorship in physics at Birkbeck College, London. He remained in that position until he retired in 1983, continuing to develop his new approach, the “pilot wave” theory.

When de Broglie postulated that tiny particles are also wave-like, he proposed the role of the waves as guiding or piloting the motions of real physical particles. Bohm fleshed out this insight by relating the pilot wave to Schrödinger’s wave function Ψ. In Bohm’s view, Ψ doesn’t collapse, but shepherds real subatomic particles into specific trajectories. This scenario yields the same results as the Schrödinger equation and resolves a great wave-particle quantum paradox. In the famous double-slit experiment , a stream of electrons or photons sent through two slits produces a pattern that could arise only from interfering waves, not particles. Bohm’s solution is that each particle traversing one of the slits rides a wave that pilots it into a complex path and generates an interference pattern from the swarm of particles.

For his part, Everett solved the measurement problem differently, as described by biographer Peter Byrne in an article , and later, a book . Born in Washington, DC, Everett showed an early interest in logical contradictions. At age twelve, he wrote to Einstein about the paradox “irresistible force meets immovable body,” and, as Everett reports, Einstein replied that there is no such paradox, but he noted Everett’s drive in attacking the problem. Everett’s father, an engineer, may have passed on his analytical abilities to his son, who graduated with honors from Catholic University as an engineer with strong backgrounds in math, operations research, and physics.

In 1953, Everett went to Princeton for graduate work. There he met Bohr, whose visit at the nearby Institute for Advanced Study sparked discussions about quantum mechanics. Later Everett said that the idea for his new theory came during a sherry-fueled session with one of Bohr’s assistants, among others. Everett was soon working out the consequences of his idea in a dissertation under John Wheeler, who had mentored Bohm and also Nobel Laureate Richard Feynman (1918–1988), and who called Everett “highly original.”

In the Copenhagen view, quantum reality as determined by the Schrödinger equation is separate from classical reality. Everett boldly asserted instead that the Schrödinger equation applies to everything, small or big, object or observer. The resulting universal wave function describes a reality without a boundary between microscopic and macroscopic or any need for the wave function to collapse. In his scheme, the measurement problem doesn’t exist.

This, however, comes at the cost of accepting a highly complex universe. If large objects and their observers obey the Schrödinger equation, then the universal wave function includes all observers and objects and their links in superposition. As Byrne explains: if the object could exist at either point A or B, in one branch of the universal wave function the observer sees the measurement result as “A,” and in another branch, a nearly identical person sees the result as “B.” (Everett called different elements of the superposition “branches.”) Further, without the jarring disruption of wave function collapse, the Schrödinger equation tells us that the branches go smoothly forward in time and do not interact, so each observer separately sees a normally unfolding macroscopic world.

In layman’s terms, this means that the universe, instead of being a unity that encompasses all reality, is filled with separate multiverses or bubbles of reality, each believed to be the entire universe by its inhabitants. The observer who saw result “A” now lives in that reality, and the person who saw “B” occupies a separately evolving reality according to their different outcome. Each of these unimaginable numbers of bubbles moves ahead into its own future, forming a totality filled with what have come to be called “parallel worlds.”

Bohr and his group scorned this grandiose idea as an answer to the measurement problem, one of his circle calling it “theology,” and another deriding Everett as “ stupid .” Wheeler had Everett rewrite his dissertation so it didn’t directly criticize the Copenhagen interpretation or its proponents. His thesis was published in 1957 and, according to Byrne, “slipped into instant obscurity.” All this should have been no surprise. As Olival Freire Jr. points out , Bohm’s earlier work—which Everett cited—had also been badly received, even with hostility, in a community dominated by Bohr and champions of the Copenhagen interpretation.

That was to change for both theories. In 1964, a bombshell result from theorist John Bell showed how to experimentally confirm the exceedingly strange quantum effect of entanglement, which Einstein called “ spooky action at a distance ”: the fact that two quantum entities can affect each other over arbitrary distances. Bell, it turns out, was strongly influenced by Bohm’s work, notes Freire. This shows that rethinking the foundations of quantum mechanics, downplayed by some physicists as only a philosophical exercise, can pay off in deep theoretical insights as well as in technology; entanglement today is used in quantum computation, communication, and cryptography.

Everett’s ideas too came to be more appreciated after The Many-Worlds Interpretation of Quantum Mechanics (Bryce DeWitt and Neill Graham, editors) was published in 1973. It included Everett’s original dissertation and related papers. This and DeWitt’s evocative phrase “many-worlds interpretation” brought new interest in Everett’s work and linked it to multiverse theory , which has been developed to solve certain problems in cosmology and as an outcome of string theory. Everett won further recognition—this time in popular culture—in 1976, when his work appeared in Analog , a leading science fiction magazine. (In fact, multiverses and parallel worlds have become staples of popular culture, as the film Everything Everywhere All at Once (2022) and the streaming series Dark Matter (2024), based on the novel by Blake Crouch, make clear.)

By 2023, Bohm’s and Everett’s seminal papers had each amassed tens of thousands of citations in the scientific literature. Surveys have also asked hundreds of physicists which interpretation of quantum mechanics they consider best. Many chose the Copenhagen view, but an equal number favor either the pilot wave or many-worlds interpretation. It’s striking that what in the 1950s were outlaw ideas, met with disbelief and antagonism, today have a significant degree of acceptance and have greatly expanded our view of the quantum world and the universe.

That Bohm and Everett could produce novel theories reflects their special circumstances and their times as well as their abilities. McCarthyism interrupted Bohm’s career but also freed him from conventional views of quantum mechanics. Historian of science Christian Forstner cites a 1981 interview in which Bohm acknowledges the upside to his departure from Princeton. It “liberated me,” Bohm admitted. “I was able to think more easily and more freely…without having to talk the language of other people.” Forstner notes that in exile, the physicist had the freedom to choose like-minded colleagues so that “the US-community and its thought-style lost importance for Bohm.” Indeed, Bohm’s exile was highly productive.

Weekly Newsletter

Get your fix of JSTOR Daily’s best stories in your inbox each Thursday.

Privacy Policy   Contact Us You may unsubscribe at any time by clicking on the provided link on any marketing message.

Everett’s expertise in operations research brought him the offer of a position with the Pentagon’s Weapons Systems Evaluation Group (WSEG) to analyze nuclear warfare after finishing his PhD. Wheeler wanted him to continue at Princeton but also knew, Byrne writes, that the lack of recognition for Everett’s ideas had left him “disappointed, perhaps bitter.” Nor did Everett enjoy truncating his thesis to mollify Bohr, and he must have realized that advocating an unpopular theory would cloud his academic career. In the end, he chose WSEG and never again worked in theoretical physics, but perhaps having this alternate possibility stiffened his resolve in presenting and defending his audacious idea. His talents shone at WSEG, but, according to Byrne, he was an alcoholic and died of a heart attack at age fifty-two.

The co-existing Copenhagen, Bohm, and Everett interpretations give the same results for many different tests of quantum behavior; and so we await the subtle experiment that distinguishes among them, showing which one is physically true and might give philosophers new insight into the nature of reality. Bohm’s and Everett’s sagas provide another valuable lesson. Science prides itself on being self-correcting; wrong theories are eventually made right, as in the old notion of a geocentric universe giving way to the modern view. The Copenhagen interpretation became unquestioned orthodoxy, but Bohm and Everett challenged it even at personal cost. That reflects the highest aspirations of science and deserves to be recognized in 2025, the upcoming International Year of Quantum Science and Technology.

Support JSTOR Daily! Join our membership program on Patreon today.

JSTOR is a digital library for scholars, researchers, and students. JSTOR Daily readers can access the original research behind our articles for free on JSTOR.

Get Our Newsletter

More stories.

• IceCube Detector Confirms Deep-Space “Ghost Particle” Phenomenon

How the Universe Forges Stars from Cosmic Clouds

The Vital Near-Magic of Fire-Eating Fungi

The Long History of Live Animal Export

Recent posts.

• The Uneven Costs of Cross-Country Connectivity
• A Potash Primer
• Lessons for American Zionism from the “Free Ireland” Cause

Support JSTOR Daily

Sign up for our weekly newsletter.

We have emailed you a PDF version of the article you requested.

Can't find the email?

Please check your spam or junk folder

You can also add [email protected] to your safe senders list to ensure you never miss a message from us.

New Quantum Engine Fueled By Ions' Entanglement

Complete the form below and we will email you a PDF version

Cancel and go back

IFLScience needs the contact information you provide to us to contact you about our products and services. You may unsubscribe from these communications at any time.

For information on how to unsubscribe, as well as our privacy practices and commitment to protecting your privacy, check out our Privacy Policy

Complete the form below to listen to the audio version of this article

Advertisement

Sign up today to get weekly science coverage direct to your inbox

© 2024 IFLScience. All Rights Reserved

Newsletters  in your inbox!

Subscribe today for our  Weekly Newsletter  in your inbox!

Quantum entanglement has enraged and baffled physicists for a century, now it might be on the verge of practical application in (very small) energy devices.

Stephen Luntz

Freelance Writer

Stephen has a science degree with a major in physics, an arts degree with majors in English Literature and History and Philosophy of Science and a Graduate Diploma in Science Communication.

Book View full profile

Book Read IFLScience Editorial Policy

Francesca Benson

Copy Editor and Staff Writer

Francesca Benson is a Copy Editor and Staff Writer with a MSci in Biochemistry from the University of Birmingham.

DOWNLOAD PDF VERSION

Quantum entanglement is no longer just a baffling feature of the subatomic world, it could enable quantum engines to produce more useful energy.

Image Credit: Vink Fan/Shutterstock.com

The strange features of quantum substances are being explored in the hope they will lead to engines more powerful and efficient than their classical counterparts. There’s still a lot we don’t understand about how the various aspects of quantum physics can help and hinder machines. A new exploration of one of quantum physics’ most distinctive features, entanglement, shows it can help boost the useful energy produced by an engine, but not the energy conversion efficiency.

Like many aspects of quantum mechanics, entanglement makes little sense to humans raised in a classical world. Einstein famously mocked it as “spooky action at a distance” – yet, eventually, the evidence for its existence became too powerful to be ignored. In the last two decades, physicists have had increasing success at entangling larger numbers of subatomic particles over increasing distances . 

Most plans for harnessing quantum entanglement for practical purposes have involved information processing and transmission, but quantum engines and quantum batteries could have a place as well. 

Last year, the first quantum engine was demonstrated , using the transformation from a fermion gas to a boson condensate and back again, instead of the differences in heat used by engines since Watt’s invention. Fermions and bosons are particles distinguished by their spins. More relevantly here, bosons can clump together much more than fermions , because the Pauli exclusion principle, which prevents two fermions occupying the same quantum state at once, doesn’t apply to them. The back and forth between an expansive fermion gas and a condensed Bose-Einstein condensate of bosons was used to drive tiny pistons.

That initial engine had an efficiency of 25 percent – a staggering achievement for a first go, but far less than the engines that drive our current world. So the race is on to make something better. Several papers have proposed using quantum entanglement, where each particle’s quantum state is inextricably linked to that of the others.

Dr Zhou Fei was part of a team that created a quantum engine based on two calcium ions in a trap, where the extent of quantum entanglement could be varied to measure its effects. The engine works on a four-stroke cycle, starting with the absorption of photons from a red laser, an expansion phase, a side-band transition to couple the system to a quantum load and finally compression. 

“Our study’s highlight is the first experimental realisation of a quantum engine with entangled characteristics. [It] quantitatively verified that entanglement can serve as a type of ‘fuel’,” Fei told the South China Morning Post . 

“We chose the entangled states of two spinning ions as the working substance, with [their] vibrational modes acting as the load. Through precise adjustments of laser frequency, amplitude, and duration, the ions were transitioned from their initial pure states to highly entangled states,” Zhou added.

The conversion efficiency, measured by the number of vibrations the engine created for each photon applied, did not improve with entanglement. However, the mechanical efficiency was higher with entanglement, meaning more useful energy was produced for the same input.

Even with increased energy, quantum engines will still have quite restricted applications. So far they only operate at temperatures close to absolute zero, for example. However, with quantum computers already needing these temperatures to work, quantum engines may fill roles associated with them, although they will need to expand significantly from this proof-of-concept.

The work is published in the journal Physical Review Letters .

ARTICLE POSTED IN

quantum entanglement,

quantum engine,

mechanical efficiency

More Space and Physics Stories

link to article

Starship Successfully Completes Fourth Test – And This Time Didn't Explode

Negative Ions Detected On Far Side Of The Moon By Instrument Aboard Chinese Lander

Russian Cosmonaut Becomes First Person To Spend 1,000 Days In Space

Can Information Escape A Black Hole?

Colossal Squid, A Titanic Trip, And Debunking Star Signs

Break It Down - The Biggest Science News Of 2024 So Far

share this!

June 6, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

peer-reviewed publication

trusted source

Study of photons in quantum computing reveals that when photons collide, they create vortices

by Weizmann Institute of Science

Vortices are a common physical phenomenon. You find them in the structure of galaxies, tornadoes and hurricanes, as well as in a cup of tea, or water as it drains from the bathtub.

Normally, vortices are formed when very fast-flowing air, water or another substance encounters an area with a slower flow. They are characterized by circular flow around a stationary axis. The role of vortices, therefore, is to bridge the tension between adjacent areas with different speed flows.

A previously unknown type of vortex has now been discovered in a study published in Science , conducted by Dr. Lee Drori, Dr. Bankim Chandra Das, Tomer Danino Zohar and Dr. Gal Winer from Prof. Ofer Firstenberg's laboratory at the Weizmann Institute of Science's Physics of Complex Systems Department.

The researchers set out to look for an efficient way of using photons to process data in quantum computers and found something unexpected: They realized that in the rare event that two photons interact, they create vortices. Not only does this discovery add to the fundamental understanding of vortices, it may ultimately contribute to the study's original goal of improving data processing in quantum computing .

The interaction between photons—light particles that also behave like waves—is only possible in the presence of matter that serves as an intermediary. In their experiment, the researchers forced photons to interact by creating a unique environment: a 10-centimeter glass cell that was completely empty, save for rubidium atoms that were so tightly packed in the center of the container that they formed a small, dense gas cloud about 1 millimeter long.

The researchers fired more and more photons through this cloud, examined their state after they had passed through it, and looked to see if they had influenced one another in any way.

"When the photons pass through the dense gas cloud, they send a number of atoms into electronically excited states known as Rydberg states," Firstenberg explains. "In these states, one of the electrons in the atom starts moving in an orbit that is 1,000 times wider than the diameter of an unexcited atom. This electron creates an electric field that influences a huge number of adjacent atoms, turning them into a kind of imaginary 'glass ball.'"

The image of a glass ball reflects the fact that the second photon present in the area cannot ignore the environment the first photon has created and, in response, it alters its speed—as if it has passed through glass.

So, when two photons pass relatively close to each other, they move at a different speed than they would have if each had been traveling alone. And when the speed of the photon changes, so does the position of the peaks and valleys of the wave it carries.

In the optimal case for the use of photons in quantum computing, the positions of the peaks and valleys become completely inverted relative to one another, owing to the influence the photons have on each other—a phenomenon known as a 180-degree phase shift.

The direction that the research took was as unique and extraordinary as the paths of the photons in the gas cloud. The study, which also included Dr. Eilon Poem and Dr. Alexander Poddubny, began eight years ago and has seen two generations of doctoral students pass through Firstenberg's laboratory.

Over time, the Weizmann scientists managed to create a dense, ultracold gas cloud, packed with atoms. As a result, they achieved something unprecedented: photons that underwent a phase shift of 180-degrees—and sometimes more.

When the gas cloud was at its densest and the photons were close to each other, they exerted the highest level of mutual influence. But when the photons moved away from each other or the atomic density around them dropped, the phase shift weakened and disappeared.

The prevalent assumption was that this weakening would be a gradual process, but researchers were in for a surprise: A pair of vortices developed when two photons were a certain distance apart. In each of these vortices, the photons completed a 360-degree phase shift and, at their center there were almost no photons at all—just as in the dark center we know from other vortices.

To understand photon vortices, think of what happens when you drag a vertically held plate through the water. The rapid movement of the water pushed by the plate meets the slower movement around it. This creates two vortices that, when viewed from above, appear to be moving together along the water's surface, but in fact, they are part of a three-dimensional configuration known as a vortex ring. The submerged part of the plate creates half a ring, which connects the two vortices visible on the surface, forcing them to move together.

Another familiar instance of vortex rings is smoke rings. In the last stages of the study, the researchers observed this phenomenon when they introduced a third photon, which added an extra dimension to the findings. The scientists discovered that the two vortices observed when measuring two photons are part of a three-dimensional vortex ring generated by the mutual influence of the three photons. These findings demonstrate just how similar the newly discovered vortices are to those known from other environments.

The vortices may have stolen the show in this study, but the researchers are continuing to work toward their goal of quantum data processing. The next stage of the study will be to fire the photons into each other and measure the phase shift of each photon separately.

Depending on the strength of the phase shifts, the photons could be used as qubits—the basic units of information in quantum computing. Unlike the units of regular computer memory, which can either be 0 or 1, quantum bits can represent a range of values between 0 and 1 simultaneously.

Journal information: Science

Provided by Weizmann Institute of Science

Explore further

Feedback to editors

A novel spray device helps researchers capture fast-moving cell processes

13 hours ago

Tropical forests adjust strategies to thrive even when soils are nutrient poor, large field experiment shows

Boeing's astronaut capsule arrives at the space station after thruster trouble

14 hours ago

New material records mechanical stress through luminescence

Computer model demonstrates desire for social proximity improves flight routes among pigeons

Schooling fish expend less energy in turbulent water compared to solitary swimmers, study finds

JWST discovers large variety of carbon-rich gases that serve as ingredients for future planets around very low-mass star

Scientists develop fatigue-free ferroelectric material

Fish out of water: How killifish embryos adapt their development

The first example of cellular origami discovered in protist

Relevant physicsforums posts, interference of two ultra short laser pulses.

Jun 5, 2024

Prism Spectrometer Objective: Optics Question

May 29, 2024

Viewing 1k x 1k slab of desert sand during extreme cold/hot temps?

May 22, 2024

How to narrow a beam to 1 mm diameter?

May 17, 2024

Questions about the Paraxial region for a single spherical surface

May 12, 2024

Collimation of a Gaussian beam

May 10, 2024

More from Optics

Related Stories

Tailoring electron vortex beams with customizable intensity patterns by electron diffraction holography

Apr 23, 2024

Physicists uses light to build complex structures

Jul 5, 2023

Scientists get photons to interact with pairs of atoms for the first time

Aug 26, 2021

Let there be light: Many photons are better than one for advancing quantum technologies

Dec 27, 2023

Singles become pairs: New insights into the light scattering of atoms

Oct 26, 2023

Quantum processor reveals bound states of photons hold strong even in the midst of chaos

Dec 7, 2022

Recommended for you

Researchers observe quantum critical Bose gas of magnons in quasi-2D antiferromagnet

21 hours ago

Calcium oxide's quantum secret: Nearly noiseless qubits

15 hours ago

Highly sensitive diamond quantum magnetometer can achieve practical ambient condition magnetoencephalography

19 hours ago

Toward testing the quantum behavior of gravity: A photonic quantum simulation

Researchers draw inspiration from ancient Alexandria to optimize quantum simulations

New model suggests partner anti-universe could explain accelerated expansion without the need for dark energy

Jun 4, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

A Groundbreaking Scientific Discovery Just Gave Humanity the Keys to Interstellar Travel

In a first, this warp drive actually obeys the laws of physics.

If a superluminal—meaning faster than the speed of light—warp drive like Alcubierre’s worked, it would revolutionize humanity’s endeavors across the universe , allowing us, perhaps, to reach Alpha Centauri, our closest star system, in days or weeks even though it’s four light years away.

However, the Alcubierre drive has a glaring problem: the force behind its operation, called “negative energy,” involves exotic particles—hypothetical matter that, as far as we know, doesn’t exist in our universe. Described only in mathematical terms, exotic particles act in unexpected ways, like having negative mass and working in opposition to gravity (in fact, it has “anti-gravity”). For the past 30 years, scientists have been publishing research that chips away at the inherent hurdles to light speed revealed in Alcubierre’s foundational 1994 article published in the peer-reviewed journal Classical and Quantum Gravity .

Now, researchers at the New York City-based think tank Applied Physics believe they’ve found a creative new approach to solving the warp drive’s fundamental roadblock. Along with colleagues from other institutions, the team envisioned a “positive energy” system that doesn’t violate the known laws of physics . It’s a game-changer, say two of the study’s authors: Gianni Martire, CEO of Applied Physics, and Jared Fuchs, Ph.D., a senior scientist there. Their work, also published in Classical and Quantum Gravity in late April, could be the first chapter in the manual for interstellar spaceflight.

POSITIVE ENERGY MAKES all the difference. Imagine you are an astronaut in space, pushing a tennis ball away from you. Instead of moving away, the ball pushes back, to the point that it would “take your hand off” if you applied enough pushing force, Martire tells Popular Mechanics . That’s a sign of negative energy, and, though the Alcubierre drive design requires it, there’s no way to harness it.

Instead, regular old positive energy is more feasible for constructing the “ warp bubble .” As its name suggests, it’s a spherical structure that surrounds and encloses space for a passenger ship using a shell of regular—but incredibly dense—matter. The bubble propels the spaceship using the powerful gravity of the shell, but without causing the passengers to feel any acceleration. “An elevator ride would be more eventful,” Martire says.

That’s because the density of the shell, as well as the pressure it exerts on the interior, is controlled carefully, Fuchs tells Popular Mechanics . Nothing can travel faster than the speed of light, according to the gravity-bound principles of Albert Einstein’s theory of general relativity . So the bubble is designed such that observers within their local spacetime environment—inside the bubble—experience normal movement in time. Simultaneously, the bubble itself compresses the spacetime in front of the ship and expands it behind the ship, ferrying itself and the contained craft incredibly fast. The walls of the bubble generate the necessary momentum, akin to the momentum of balls rolling, Fuchs explains. “It’s the movement of the matter in the walls that actually creates the effect for passengers on the inside.”

Building on its 2021 paper published in Classical and Quantum Gravity —which details the same researchers’ earlier work on physical warp drives—the team was able to model the complexity of the system using its own computational program, Warp Factory. This toolkit for modeling warp drive spacetimes allows researchers to evaluate Einstein’s field equations and compute the energy conditions required for various warp drive geometries. Anyone can download and use it for free . These experiments led to what Fuchs calls a mini model, the first general model of a positive-energy warp drive. Their past work also demonstrated that the amount of energy a warp bubble requires depends on the shape of the bubble; for example, the flatter the bubble in the direction of travel, the less energy it needs.

THIS LATEST ADVANCEMENT suggests fresh possibilities for studying warp travel design, Erik Lentz, Ph.D., tells Popular Mechanics . In his current position as a staff physicist at Pacific Northwest National Laboratory in Richland, Washington, Lentz contributes to research on dark matter detection and quantum information science research. His independent research in warp drive theory also aims to be grounded in conventional physics while reimagining the shape of warped space. The topic needs to overcome many practical hurdles, he says.

Controlling warp bubbles requires a great deal of coordination because they involve enormous amounts of matter and energy to keep the passengers safe and with a similar passage of time as the destination. “We could just as well engineer spacetime where time passes much differently inside [the passenger compartment] than outside. We could miss our appointment at Proxima Centauri if we aren’t careful,” Lentz says. “That is still a risk if we are traveling less than the speed of light.” Communication between people inside the bubble and outside could also become distorted as it passes through the curvature of warped space, he adds.

While Applied Physics’ current solution requires a warp drive that travels below the speed of light, the model still needs to plug in a mass equivalent to about two Jupiters. Otherwise, it will never achieve the gravitational force and momentum high enough to cause a meaningful warp effect. But no one knows what the source of this mass could be—not yet, at least. Some research suggests that if we could somehow harness dark matter , we could use it for light-speed travel, but Fuchs and Martire are doubtful, since it’s currently a big mystery (and an exotic particle).

Despite the many problems scientists still need to solve to build a working warp drive, the Applied Physics team claims its model should eventually get closer to light speed. And even if a feasible model remains below the speed of light, it’s a vast improvement over today’s technology. For example, traveling at even half the speed of light to Alpha Centauri would take nine years. In stark contrast, our fastest spacecraft, Voyager 1—currently traveling at 38,000 miles per hour—would take 75,000 years to reach our closest neighboring star system.

Of course, as you approach the actual speed of light, things get truly weird, according to the principles of Einstein’s special relativity . The mass of an object moving faster and faster would increase infinitely, eventually requiring an infinite amount of energy to maintain its speed.

“That’s the chief limitation and key challenge we have to overcome—how can we have all this matter in our [bubble], but not at such a scale that we can never even put it together?” Martire says. It’s possible the answer lies in condensed matter physics, he adds. This branch of physics deals particularly with the forces between atoms and electrons in matter. It has already proven fundamental to several of our current technologies, such as transistors, solid-state lasers, and magnetic storage media.

The other big issue is that current models allow a stable warp bubble, but only for a constant velocity. Scientists still need to figure out how to design an initial acceleration. On the other end of the journey, how will the ship slow down and stop? “It’s like trying to grasp the automobile for the first time,” Martire says. “We don’t have an engine just yet, but we see the light at the end of the tunnel.” Warp drive technology is at the stage of 1882 car technology, he says: when automobile travel was possible, but it still looked like a hard, hard problem.

The Applied Physics team believes future innovations in warp travel are inevitable. The general positive energy model is a first step. Besides, you don’t need to zoom at light speed to achieve distances that today are just a dream, Martire says. “Humanity is officially, mathematically, on an interstellar track.”

Before joining Popular Mechanics , Manasee Wagh worked as a newspaper reporter, a science journalist, a tech writer, and a computer engineer. She’s always looking for ways to combine the three greatest joys in her life: science, travel, and food.

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Physics .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

The Source of All Consciousness May Be Black Holes

Immortality Is Impossible Until We Beat Physics

How a Lunar Supercollider Could Upend Physics

Is Consciousness Everywhere All at Once?

One Particle Could Shatter Our Concept of Reality

Do Black Holes Die?

Are Multiverse Films Like ‘The Flash’ Realistic?

Why Time Reflections Are a ‘Holy Grail’ in Physics

Why Our Existence Always Contains Some Uncertainty

Copies of You Could Live Inside Quantum Computers

There’s an ‘Anti-Universe’ Going Backward in Time