algorithm for travelling salesman

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, ($O(2^n n^2)$), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is $O(n!)$, which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are $4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24$ different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

Check the length of every possible route, one route at a time.
Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

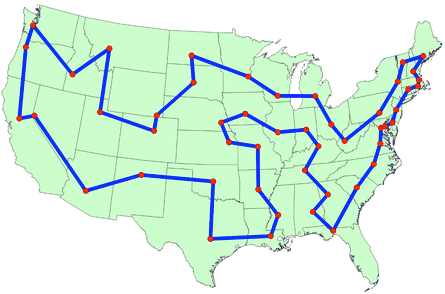
Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

Visit every city.
The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of $O(n^2) $.

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is $O(n!)$, like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as $4 \cdot 3 \cdot 2 \cdot 1 = 24$. And for just 12 cities for example, there are $12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600$ possible routes!

See the time complexity for the greedy algorithm $O(n^2)$, versus the time complexity for finding the shortest route by comparing all routes $O(n!)$, in the image below.

Time complexity for checking all routes versus running a greedy algorithm and finding a near-optimal solution instead.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from $n!$ to $(n-1)!$.

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually $ \frac{(n-1)!}{2}$.

But even if we can reduce the number of routes we need to check to $ \frac{(n-1)!}{2}$, the time complexity is still $ O(n!)$, because for very big $n$, reducing $n$ by one and dividing by 2 does not make a significant change in how the time complexity grows when $n$ is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Travelling Salesman Problem (Greedy Approach)

Travelling salesperson algorithm.

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

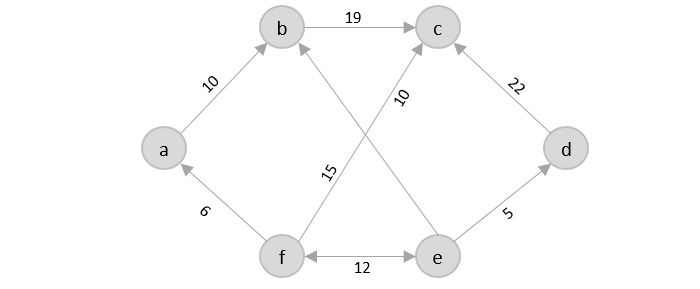
There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G’) which will record the path the salesman is going to take from one node to another.

The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Consider the following graph with six cities and the distances between them −

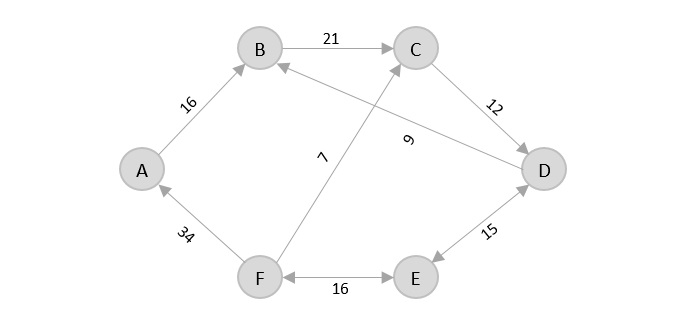
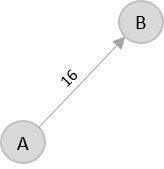
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

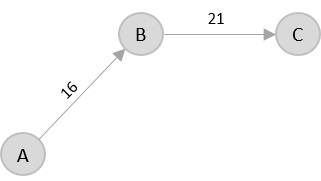
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

There’s only one edge between C → D, therefore it is added to the output graph.

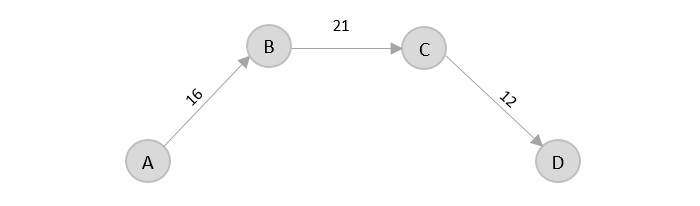
There’s two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

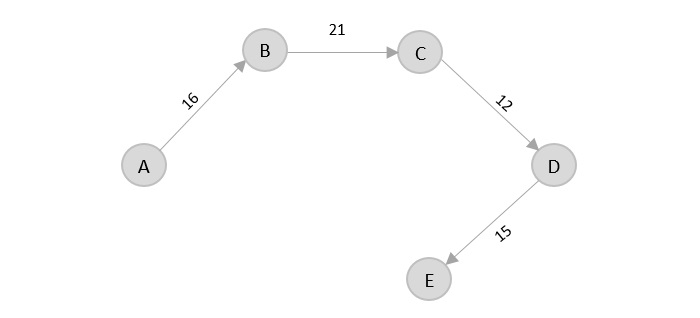
There’s only one edge from e, that is E → F. Therefore, it is added into the output graph.

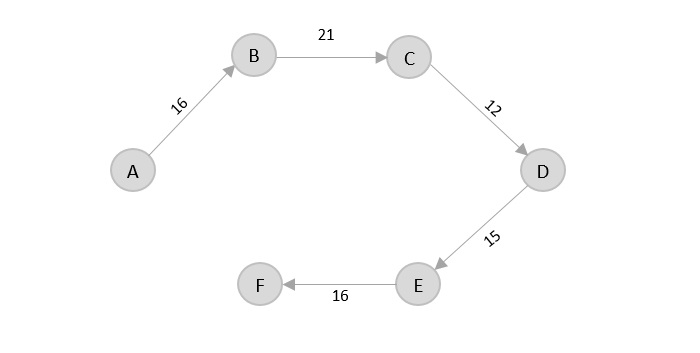
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

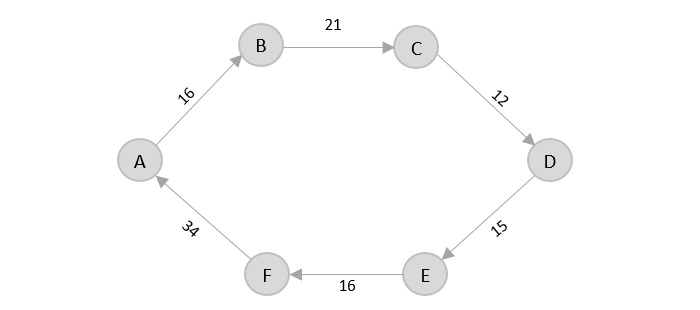
The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

Learning center series

Travelling salesman problem explained

Published on April 26, 2024
by Oguzhan Uyar
Last updated: 2 months ago

Revolutionize your understanding of the Travelling Salesman Problem (TSP); a mind-boggling conundrum that has compelled academia and industry alike. In the upcoming lines, we decode the key concepts, algorithms, and anticipated solutions for 2024 to this age-old dilemma.

Now, picture the TSP as a globetrotting traveling salesman who’s whirlwind journey. He must stop at every city once, only the origin city once, and find the quickest shortest possible route back home. If daunting to visualize, consider this: the possible number of routes in the problem concerning just 20 cities exceeds the number of atoms in the observable universe.

Fathom the sheer magnitude?

So, what is the Travelling Salesman Problem, and why has it remained unsolved for years? Let’s snap together the puzzle of this notorious problem that spans mathematics, computer science, and beyond. Welcome to an insightful voyage into the astonishing world of the TSP. Delve deeper into how optimizing travel routes can transform the efficiency of solving the Travelling Salesman Problem, marking a milestone in the journey toward more effective logistics and navigational strategies.

Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms

Defining the travelling salesman problem: a comprehensive overview.

The Travelling Salesman Problem, often abbreviated as TSP, has a strong footing in the realm of computer science. To the untrained eye, it presents itself as a puzzle: a salesperson or traveling salesman must traverse through a number of specific cities before an ending point and return to their ending point as of origin, managing to do so in the shortest possible distance. But this problem is not simply a conundrum for those fond of riddles; it holds immense significance in the broad field of computer science and optimization. Optimizing travel routes is the key to solving the Travelling Salesman Problem efficiently, ensuring the shortest and most cost-effective journey for salespeople or travelers.

The sheer computational complexity of TSP is what sets it apart, and incidentally, why it is considered a challenging problem to solve. Its complexity derives from the factorial nature of the problem: whenever a new city is added, the total number of possibilities increases exponentially. Thus, as the problem scope enlarges, it swiftly becomes computationally prohibitive to simply calculate all possible solutions to identify an optimal shortest route through. Consequently, developing effective and efficient algorithms to solve the TSP has become a priority in the world of computational complexity.

Polynomial Time Solution: The TSP can be solved by a deterministic Turing machine in polynomial time, which means that the number of steps to solve the problem can be at most 1.5 times the optimal global solution.

One such algorithm is the dynamic programming approach that can solve TSP problems in polynomial time. The approach uses a recursive formula to compute the shortest possible route that visits all other nodes in the cities exactly once and ends at all nodes in the starting point or city. Moreover, linear programming and approximation algorithms have also been used to find near-optimal solutions. Discover how dynamic programming and other strategies serve as algorithms for optimizing routes , enhancing efficiency in plotting course paths.

Unraveling TSP Algorithms: From Brute Force to Heuristics

A multitude of algorithms have been developed to contend with the TSP. The brute force method, for example, entails considering the shortest distance for all possible permutations of cities, calculating the total distance for six cities along each route, and selecting the shortest distance for one. While brute force promises an optimal solution, it suffers from exponential computational complexity, rendering it unfeasible for large datasets.

TSP Complexity: A TSP with just 10 cities has 362,880 possible routes , making brute force infeasible for larger instances.

On the other hand, we have heuristic algorithms that generate good, albeit non-optimal, solutions in reasonable timeframes. The greedy algorithm, for instance, initiates from a starting city and looks for the shortest distance from other nodes to the next node minimizes the distance, and guarantees speed but is not necessarily an optimal solution.

Algorithmic Potential: Local Solutions 4/3 Times Optimal Global: The theoretical conjecture suggests an algorithm that can provide a local solution within 4/3 times the optimal global solution.

Record Local TSP Solution: The record for a local solution to the Traveling Salesman Problem (TSP) is 1.4 times the optimal global solution, achieved in September 2012 by Andr´as Seb˝o and Jens Vygen.

Exploring further, we encounter more refined heuristic solutions such as the genetic algorithm and simulated annealing algorithm. These algorithms deploy probabilistic rules, with the former incorporating principles of natural evolution and the latter being inspired by the cooling process in metallurgy. They differ significantly from each other in terms of how they search for solutions, but when compared to brute force, they often offer a promising trade-off between quality and computational effort.

Certainly, the TSP is far more than a problem to puzzle over during a Sunday afternoon tea. It’s a complex computational task with real-world implications, and unraveling it requires more than brute force; it demands the application of sophisticated algorithms designed to balance efficiency and quality of results. Nevertheless, with a better understanding of the problem statement and its dynamics, you can unlock the potential to not just solve problems faster, but to do so more intelligently.

Delivery notifications and tracking improve customer satisfaction by 27%.

Metrobi automatically notifies your receivers of ETAs, provides delivery tracking, and collects delivery feedback.

Practical Solutions to the Travelling Salesman Problem

Implementing tsp solutions: a step-by-step guide, a comprehensive process for implementing tsp solutions.

Developing complete, practical solutions for the Travelling Salesman Problem (TSP) requires a good grasp of specific algorithms. Visual aids, for example, such as finding all the edges leading out of a given city, can help to simplify the process. Enhance your ability to solve the Travelling Salesman Problem by mastering route optimization with Google Maps , streamlining your path and saving significant time on the go.

TSP's Computer Science Quest for Shortest Routes: The TSP involves finding the shortest route to visit a set of cities exactly once before returning to the starting city, aiming to minimize travel distance.

Travelling Salesman Problem Explained - Travelling Salesman Problem -

One popular approach to TSP problem solving is the dynamic programming approach, which involves breaking down the problem into smaller sub-problems and recursively solving them. Other approaches include approximation algorithms, which generate near-optimal solutions to small problems in polynomial time, and bound algorithms, which aim to find an upper bound on the optimal solution given graph top. Discover how software for planning routes can revolutionize your approach to the TSP problem, offering near-optimal solutions that enhance efficiency and effectiveness in logistical planning.

TSP Variants: ASTP and STSP The TSP can be divided into two types: the asymmetric traveling salesman problem (ASTP) and the symmetric traveling salesman problem (STSP)

Practical code implementation

Before diving into code manipulations, it’s worth noting that practical implementation varies based on the specifics of the problem and the chosen algorithm. Let’s further deconstruct these notions by examining the steps for code implementation for a pre-determined shortest path first. It’s crucial to efficiently concede each point of the shortest path, call other nodes, connect each node, and conclude each route. Hereby, I shall delve into the practicalities of coding from an output standpoint, concentrating on readability, scalability, and execution efficiency. Uncover how optimizing routes can elevate your coding practices for more efficient, scalable, and readable solutions in logistics and transportation.

TSP Instance Size: The size of the TSP instances used in the studies is 100 nodes.

Cluster Quantity in TSP Instances: The number of clusters in the TSP instances used in the studies is 10 .

The Quantity of Instances per Cluster in Studies: The number of instances in each cluster used in the studies is 100.

Optimizing TSP Solutions: Tips and Tricks

Tsp solutions optimization techniques.

An optimized solution for the TSP is often accomplished using advanced algorithms and techniques. Optimization techniques allow professionals to solve more intricate problems, rendering them invaluable tools when handling large datasets and attempting to achieve the best possible solution. Several approaches can be taken, such as heuristic and metaheuristic approaches, that can provide near-optimal solutions with less use of resources. Discover the key to enhancing your logistics operations by mastering the art of optimizing delivery routes , thereby achieving efficiency and reducing costs significantly.

Expert Advice for Maximum Efficiency Minimum Cost

Even the most proficient problem solvers can gain from learning expert tips and tricks. These nuggets of wisdom often provide the breakthrough needed to turn a good solution into a great one. The TSP is no exception. Peering into the realm of experts can provide novel and creative ways to save time, increase computation speed, manage datasets, and achieve the most efficient shortest route around.

By comprehending and implementing these solutions to the Travelling Salesman Problem, one can unravel the complex web of nodes and paths. This equips any problem-solver with invaluable insights that make navigating through real-world TSP applications much more manageable. By adopting sophisticated routing planner software , businesses can significantly streamline their delivery operations, ensuring a more predictable and cost-effective way of dealing with the challenges presented by the Travelling Salesman Problem.

Real-World Applications of the Travelling Salesman Problem

Tsp in logistics and supply chain management.

The Travelling Salesman Problem (TSP) is not confined to theoretical mathematics or theoretical computer science either, it shines in real-world applications too. One of its most potent applications resides in the field of logistics and supply chain management. Explore how the latest gratis route planning applications can revolutionize logistics and supply chain efficiency by uncovering the top 10 free software tools for 2024.

With globalization, the importance of more efficient routes for logistics and supply chain operations has risen dramatically. Optimizing routes and decreasing costs hold the key to success in this arena. Here’s where TSP comes into play. Discover how Planning for Multiple Stops can revolutionize your logistics, ensuring the most efficient paths are taken. Dive into our post to see how it streamlines operations and reduces expenses.

In the vast complexity of supply chain networks, routing can be a colossal task. TSP algorithms bring clarity to the chaos, eliminating redundant paths and pointing to the optimal route covering the most distance, shortest path, and least distance between all the necessary points—leading to a drastic dip in transportation costs and delivery times. Uncover how optimizing delivery routes can revolutionize your logistics, ensuring efficiency and cost-effectiveness in your delivery operations.

Real-World Examples

Consider the case of UPS – the multinational package delivery company. They’ve reportedly saved hundreds of millions of dollars yearly by implementing route optimization algorithms originating from the Travelling Salesman Problem. The solution, named ORION, helped UPS reduce the distance driven by their drivers roughly by 100 million miles annually. Understand the intricacies of the problem of routing vehicles to appreciate how businesses like UPS can significantly benefit from efficient logistical strategies and route optimization systems.

TSP in GIS and Urban Planning: Optimal Route

TSP’s contributions to cities aren’t confined to logistics; it is invaluable in Geographic Information Systems (GIS) and urban planning as well. A city’s efficiency revolves around transportation. The better the transport networks and systems, the higher the city’s productivity. And as city authorities continuously strive to upgrade transportation systems, they find an ally in TSP. Discover how TSP enhances road architecture by integrating specialized truck routing solutions , elevating urban transport strategies.

Advanced GIS systems apply TSP to design more efficient routes and routing systems for public transportation. The aim of the route is to reach maximum locations with the least travel time and least distance, ensuring essential amenities are accessible to everyone in the city. Discover how dynamic routing optimization can enhance city-wide transportation efficiency and accessibility for all residents.

The city of Singapore, known for its efficient public transportation system, owes part of its success to similar routing algorithms. The Land Transport Authority uses TSP-related solutions to plan bus routes, reducing travel durations and enhancing accessibility across the city.

Delving Deeper: The Complexity and History of the Travelling Salesman Problem

Understanding the complexity of tsp.

TSP is fascinating not just for its inherent practicality but also for the complexity it brings along. TSP belongs to a class of problems known as NP-hard, a category that houses some of the most complex problems in computer science. But what makes TSP so gnarled?

Unravel the Intricacies: Why is TSP complex?

TSP is a combinatorial optimization problem, which simply means that it’s all about figuring out the most often optimal solution among a vast number of possible solutions or combinations of approximate solutions. The real challenge comes from an innocent-sounding feature of TSP: As the number of cities (we call them nodes) increases, the complexity heightens exponentially, not linearly. The number of possible routes takes a dramatic upward turn as you add more nodes, clearly exemplifying why TSP is no walk-in-the-park problem. Discover how leveraging multi-stop itinerary planning can transform this complex task, offering a streamlined solution to navigate through the myriad of possibilities efficiently.

NP-hard and TSP: A Connection Explored

In computer science, we use the terms P and NP for classifying problems. P stands for problems where a solution can be found in ‘polynomial time’. NP stands for ‘nondeterministic polynomial time’, which includes problems where a solution can be verified in polynomial time. The concept of ‘NP-hardness’ applies to TSP. Any problem that can be ‘reduced’ to an NP problem in polynomial time is described as NP-hard. In simpler terms, it’s harder than the hardest problems of NP. TSP holds a famed position in this class, making it a noteworthy example of an NP-hard problem. Discovering efficient solutions for the Traveling Salesman Problem (TSP) exemplifies how optimizing routes can streamline complex logistical challenges, showcasing the practical impact of advancements in algorithmic route optimization.

A Look Back: The History of the Travelling Salesman Problem

TSP is not a new kid on the block. Its roots can be traced back to the 1800s, and the journey since then has been nothing short of a compelling tale of mathematical and computational advancements.

The Origins and Evolution of TSP

Believe it or not, the Travelling Salesman Problem was first formulated as a mathematical problem in the 1800s. This was way before the advent of modern computers. Mathematicians and logisticians were intrigued by the problem and its implications. However, it wasn’t until the mid-20th century that the problem started to gain more widespread attention. Over the years, the TSP has transformed from a theoretical model to a practical problem that helps solve real-world issues.

A Classic Shortest Route Problem Since 1930s: The TSP is a classic optimization problem within the field of operations research, first studied during the 1930s.

Milestones in TSP Research

Looking at all the cities and milestones in TSP research, the story is truly impressive. From some of the initial heuristic algorithms to solve smaller instances of TSP, to geometric methods and then approximation algorithms, TSP research has seen a lot. More recently, we have also seen practical solutions to TSP using quantum computing — a testament to how far we’ve come. Each of these milestones signifies an innovative shift in how we understand and solve TSP. Discovering the top delivery route planning software in 2024, we navigated through the advancements in TSP solutions to identify which applications excel in streamlining delivery logistics.

Wrapping Up The Journey With Algorithms and Solutions

The Travelling Salesman Problem (TSP) remains a complex enigma of business logistics, yet, the advent of sophisticated algorithms and innovative solutions are paving avenues to optimize routing, reduce travel costs further, and enhance customer interactions.

Navigating the TSP intricacies is no longer a daunting challenge but a worthwhile investment in refining operational efficiency and delivering unparalleled customer experiences. With advanced toolsets and intelligent systems, businesses are closer to making more informed, strategic decisions. Elevate your logistical operations and customer satisfaction with the strategic integration of route scheduling solutions .

Now, it’s your turn. Reflect on your current logistics complexities. How can your business benefit from implementing these key concepts and algorithms? Consider where you could incorporate these practices to streamline and revolutionize your daily operations.

Remember, in the world of dynamic business operations, mastering the TSP is not just an option, but a strategic imperative. As you move forward into 2024, embrace the art of solving the TSP. Unravel the potential, decipher the complexities, and unlock new horizons for your business.

Ready for the challenge?

What is route optimization?

Top route optimization algorithms

What is multi-stop route planning and why is it important?

What is multi stop route planning and why is it important?

How to optimize routes with Google Maps

7 benefits of using route scheduling software

Benefits of using route scheduling software

Why delivery route optimization is crucial

What does a route planning software do?

Truck route planning vs common route planning

‟I am able to do twice as many orders because I don't spend time delivering”

‟The quality of customer service is great!”

‟My favorite drivers are there for me”

Field Trip Flowers

‟I've got a partner to help me grow, succeed and expand”

Gonzalez Y Gonzalez

Route Optimization
travelling salesman problem

dynamic route optimization

vehicle routing problem

free route planning software

truck route

route planning software

Shopify Local Delivery
best shopify delivery apps

Become A Floral Designer
floral designer

Small Business Finances
small business cash flow management

Tips for better small business cash flow management

Retail Industry Legislation and Policies
retail compliance

Small Business Metrics
small business metrics

Customer Relations
retail customer complaints

Types of Shipping Methods
International shipping

Click and collect shipping

omnichannel logistics

Last Mile Delivery Glossary
green transportation

Benefits of green transportation to your business

payload capacity

Success Stories

Dorchester Brewing Company

Rebel Bread

LuNo Culinary

Smart Lunches

Wicked Bagel

DELIVER WITH METROBI

Grow with confidence

Atlanta courier service
Austin courier service
Boston courier service
Chicago courier service
Denver courier service
Miami courier service
New York City courier service
Los Angeles courier service
Philadelphia courier service
San Francisco courier service
Washington DC courier service
See all locations
Driver Network
Software Only

55 Court St, Boston, MA 02108
[email protected]
Team Metrobi
Privacy policy
Terms of service
Write for us NEW

Refer us to a company, you earn $250 and they earn $250. Learn more

Delivery Management Software
Shopify Delivery Planner App
Metrobi Delivery API NEW
Zapiet: Pickup Delivery NEW
See all integrations
Metrobi vs. Onfleet
Metrobi vs. Roadie
Metrobi vs. Roadie Support
See all comparisons
Bulk Order Delivery Service
Express Urgent Delivery Service
Fixed Route Delivery Service
On Demand Delivery Service
Overnight Delivery Service
Same Day Delivery Service
Scheduled Delivery Service
Wholesale Delivery Service
See all delivery services
Artisan Food
Food Producers
See all industries

Want to access our large pool of drivers?

We started Metrobi to take operations off your plate. We provide drivers (rated 4.97/5), dedicated operation managers (70% cheaper), and routing software with a receiver notification system.

elogii-route-optimization-software-side-banner

Home > Blog > Travelling Salesman Problem: Definition, Algorithms & Solutions

Travelling Salesman Problem: Definition, Algorithms & Solutions

Explore the Traveling Salesman Problem, its algorithms, real-world applications, and practical solutions for optimizing delivery routes in logistics.

The Traveling Salesman Problem (TSP) is all about figuring out the shortest route for a salesperson to visit several cities, starting from one place and possibly ending at another. It's a well-known problem in computer science and operations research, with real-world uses in logistics and delivery.

There are many possible routes, but the goal is to find the one that covers the least distance or costs the least. This is what mathematicians and computer scientists have been working on for decades.

This isn’t just a theory problem. Using route optimization algorithms to find better routes can help delivery businesses make more money. It also helps to lower their greenhouse gas emissions by traveling less.

In theoretical computer science, the Traveling Salesman Problem (TSP) gets a lot of attention because it’s simple to explain but tough to solve. It’s a type of problem called combinatorial optimization and is known as NP-hard. This means the number of possible routes grows very quickly as more cities are added. Since there isn’t an efficient algorithm to solve TSP quickly, computer scientists use approximation algorithms. These methods test many different routes and pick the shortest one that costs the least.

You can solve the main problem by trying every possible route and picking the best one, but this brute-force method gets tricky as you add more destinations. The number of possible routes grows quickly, quickly overwhelming even the fastest computers. For just 10 destinations, there are over 300,000 possible routes. When there are 15 destinations, the number of routes can skyrocket to over 87 billion.

For bigger real-world Traveling Salesman Problems, tools like Google Maps Route Planner or Excel just don’t cut it anymore. Businesses turn to approximate solutions using quick TSP algorithms that use smart shortcuts. Trying to find the exact best route with dynamic programming isn’t usually practical for large problems.

In this post:

Three Common Algorithms for the Traveling Salesman Problem

Academic solutions for the traveling salesman problem, real-world uses of the traveling salesman problem, practical solutions for tsp and vrp, faqs about the travelling salesman problem.

boost-efficiency-wih-route-optimization-software-desktop

1. Brute-Force Method

The brute-force method, sometimes called the naive approach, tries every possible route to find the shortest one. To use this method, you list all possible routes, calculate the distance for each one, and then pick the shortest route as the best solution.

This method works only for small problems and is mostly used for teaching in theoretical computer science. For larger problems, it's not practical.

2. Branch and Bound Method

The branch and bound method starts with an initial route, usually from the start point to the first city. It then explores different ways to extend the route by adding one city at a time. For each new route, it checks the length and compares it to the best route found so far. If the current route is longer than the best one, the algorithm "prunes" or cuts off that route, since it won’t be the best solution.

This pruning helps make the algorithm more efficient by focusing only on the most promising routes. The process continues until all possible routes have been checked, and the shortest one is chosen as the best solution. Branch and bound is a smart way to handle tough problems like the traveling salesman problem.

3. Nearest Neighbor Method

The nearest neighbor algorithm starts from a random point. From there, it finds the closest city that hasn't been visited yet and adds it to the route. This process is repeated by moving to the next closest unvisited city until all cities are included in the route. Finally, the route loops back to the starting city to complete the tour.

Although the nearest neighbor method is simple and fast, it often doesn't find the best possible route. For large or complex problems, it might end up with a route much longer than the optimal one. Still, it’s a useful starting point for solving the traveling salesman problem and can quickly provide a good enough solution.

This approach can also be used as the first step to create a decent route, which can then be improved with more advanced algorithms to get an even better solution.

Researchers have been working for years to find the best solutions for the Traveling Salesman Problem. Here are some of the recent advancements:

Machine Learning for Vehicle Routing . MIT researchers use machine learning to tackle large, complex problems by breaking them into smaller, more manageable ones.
Zero Suffix Method . Developed by researchers in India, this technique addresses the classical symmetric Traveling Salesman Problem.
Biogeography-Based Optimization Algorithm . Inspired by animal migration patterns, this method uses nature's strategies to find optimization solutions.
Meta-Heuristic Multi-Restart Iterated Local Search (MRSILS) . This approach claims to be more effective than genetic algorithms when working with clusters.
Multi-Objective Evolutionary Algorithm . Based on the NSGA-II framework, this method solves multiple Traveling Salesman Problems simultaneously.
Multi-Agent System . This system handles the Traveling Salesman Problem for N cities with fixed resources.

Even though solving the Traveling Salesman Problem is complex, approximate solutions—often using artificial intelligence and machine learning—are valuable across many industries.

For instance, TSP solutions can enhance efficiency in last-mile delivery. Last-mile delivery is the final stage in the supply chain, where goods move from a warehouse or depot to the customer. This step is also the biggest cost factor in the supply chain. It typically costs about $10.10, while customers only pay around $8.08, with companies covering the difference to stay competitive. Reducing these costs can significantly boost business profitability.

Reducing costs in last-mile delivery is a lot like solving a Vehicle Routing Problem (VRP) . VRP is a broader version of the Travelling Salesman Problem and is a key topic in mathematical optimization. Instead of finding just one best route, VRP focuses on finding the most efficient set of routes. It might involve multiple depots, many delivery locations, and several vehicles. Like the Travelling Salesman Problem, finding the best solution for VRP is also a tough challenge.

Academic solutions for the Traveling Salesman Problem (TSP) and Vehicle Routing Problem (VRP) aim to find the perfect answer to these tough problems. However, these solutions often aren't practical for real-world issues, especially when dealing with last-mile logistics.

Academic solvers focus on perfection, which means they can take a long time—sometimes hours, days, or even years—to compute the best solutions. For a delivery business that needs to plan routes every day , waiting that long isn't feasible. They need quick results to get their drivers and goods moving as soon as possible. Many businesses turn to tools like Google Maps Route Planner for a faster option.

In contrast, real-life TSP and VRP solvers use route optimization algorithms that provide near-perfect solutions in much less time. This allows delivery businesses to plan routes efficiently and swiftly, keeping their operations running smoothly.

What is a Hamiltonian cycle, and why is it key to the Travelling Salesman Problem?

A Hamiltonian cycle is a route in a graph that visits every point (vertex) exactly once before returning to where it started. It's essential for solving the Travelling Salesman Problem (TSP) because TSP is about finding the shortest Hamiltonian cycle that minimizes the total travel distance or time.

How does linear programming help with the Travelling Salesman Problem?

Linear programming (LP) is a mathematical technique used to optimize a linear function while meeting certain constraints. For the TSP, LP is useful for creating and solving a simpler version of the problem to find bounds or approximate solutions. It often involves relaxing some constraints, like integer constraints, to make the problem easier to handle.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion is a method where a function solves a problem by breaking it down into smaller, similar problems and calling itself to handle these smaller problems. In the context of the TSP, recursion is used in approaches like "Divide and Conquer," which breaks the main problem into smaller parts, making it easier to solve. This helps reduce repetitive calculations and speeds up finding a solution.

Why is time complexity important for understanding the Travelling Salesman Problem?

Time complexity measures how the time required to solve a problem grows as the size of the problem increases. For the Travelling Salesman Problem, knowing the time complexity is important because it helps estimate how long different algorithms will take, especially since TSP is NP-hard. As the number of cities grows, finding a solution can become very slow and challenging.

How to Boost Profitability and Efficiency with a Sales Route Planner

Boost sales efficiency and profits with our route planner. Optimize routes, prioritize leads, and streamline field sales operations for maximum...

Distribution Center Processes and Best Practices You Need to Know

Discover key distribution center practices, from receiving to last-mile coordination. Enjoy a seamless supply chain and enhanced customer...

The leading Route Optimization resource

Be the first to know when new articles are released. eLogii has a market-leading blog and resources centre designed specifically to help business across countless distribution and field-services sub sectors worldwide to succeed with actionable content and tips.

Algorithms for the Travelling Salesman Problem

Printables.com

The Travelling Salesman Problem (TSP) is a classic algorithmic problem in the field of computer science and operations research, focusing on optimization. It seeks the shortest possible route that visits every point in a set of locations just once.
The TSP problem is highly applicable in the logistics sector , particularly in route planning and optimization for delivery services. TSP solving algorithms help to reduce travel costs and time.
Real-world applications often require adaptations because they involve additional constraints like time windows, vehicle capacity, and customer preferences.
Advances in technology and algorithms have led to more practical solutions for real-world routing problems. These include heuristic and metaheuristic approaches that provide good solutions quickly.
Tools like Routific use sophisticated algorithms and artificial intelligence to solve TSP and other complex routing problems, transforming theoretical solutions into practical business applications.

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest possible route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one — the one that will require the least distance or cost — is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem in graph theory. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm for solving travelling salesman problems in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

A random scattering of 22 black dots on a white background.

The main problem can be solved by calculating every permutation using a brute force approach, and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially, soon surpassing the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

The same 22 black dots, joined by a single black line in a continuous loop. The resulting shape is an irregular polygon.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

TThe brute-force approach, also known as the naive approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the brute-force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one — this is the optimal solution.

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route beyond the first pair of cities, one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the traveling salesman problem.

3. The nearest neighbor method

To implement the nearest neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the nearest neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the nearest neighbor algorithm serves as a good starting point for tackling the traveling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition. ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP.
Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization.
Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used.
Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II.
Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource.

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, approximate solutions — often produced using artificial intelligence and machine learning — are useful in all verticals.

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.

The same field of dots from the last images, now in three groups each joined by a single continuous loop. The three loops meet in the middle so that the image looks almost like a flower with three oddly-shaped petals.

Minimizing costs in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

What is a hamiltonian cycle, and why is it important in solving the travelling salesman problem.

A Hamiltonian cycle is a complete loop that visits every vertex in a graph exactly once before returning to the starting vertex. It's crucial for the TSP because the problem essentially seeks to find the shortest Hamiltonian cycle that minimizes travel distance or time.

What role does linear programming play in solving the Travelling Salesman Problem?

Linear programming (LP) is a mathematical method used to optimize a linear objective function, subject to linear equality and inequality constraints. In the context of TSP, LP can help in formulating and solving relaxation of the problem to find bounds or approximate solutions, often by ignoring the integer constraints (integer programming being a subset of LP) to simplify the problem.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion involves a function calling itself to solve smaller sub-problems of the same type as the larger problem. In TSP, recursion is used in methods like the "Divide and Conquer" strategy, breaking down the problem into smaller, manageable subsets, which can be particularly useful in dynamic programming solutions. It reduces redundancy and computation time, making the problem more manageable.

Why is understanding time complexity important when studying the Travelling Salesman Problem?

Time complexity refers to the computational complexity that describes the amount of computer time it takes to solve a problem. For TSP, understanding time complexity is crucial because it helps predict the performance of different algorithms, especially given that TSP is NP-hard and solutions can become impractically slow as the number of cities increases.

Liked this article? See below for more recommended reading!

A man wearing a red T-shirt with the word "Delivery" across the front stands at the open door of a van. He is holding a small package and looking at his watch.

Solving the Vehicle Routing Problem (2024)

Decorative graphic repeating the post title with a Google Maps screenshot.

How To Optimize Multi-Stop Routes With Google Maps (2024)

Photograph of a rural scene that suggests the Alps. In the foreground is a green meadow with a scattering of purple wildflowers and some trees, sloping down to a collection of small huts or cabins on a piece of level ground. In the background are snow-capped mountains.

How Route Optimization Impacts Our Earth

Key Products

Route Optimization API

Optimize routing, task allocation and dispatch

Directions and Distance Matrix API

Calculate accurate ETAs, distances and directions

Navigation API & SDKs

Provide turn-by-turn navigation instructions

Live Tracking API & SDKs

Track and manage assets in real time

All Products

Product Demos

See NextBillion.ai APIs & SDKs In action

Integrations

Easily integrate our products with your tools

Platform Overview

Learn about how Nextbillion.ai's platform is designed

Routing Customizations

Learn about NextBillion.ai's routing & map customizations capabilities

Supply Chain & Logistics

Get regulation-compliant truck routes

Fleet Management

Solve fleet tracking, routing and navigation

Last-Mile Delivery

Maximize fleet utilization with optimal routes

On-Demand Delivery

Real-time ETA calculation

Middle Mile Delivery

Real-time ETA Calculation

Ride Hailing

Optimized routes for cab services

Non-Emergency Medical Transport

Optimize routing and dispatch

Field Workforce

Field Services

Automate field service scheduling

Waste Collection

Efficient route planning with road restrictions

BY BUSINESS TYPE

Logistics technology providers

Fleet owners

BY LOGISTICS TYPE

Long haul trucking

Middle-mile logistics

Last-mile delivery

Urban mobility

Field services

Non-emergency transportation

See NextBillion.ai APIs & SDKs in Action

Case Studies

Discover what customers are building in real time with NextBillion.ai

Get in-depth and detailed insights

Product Updates

Latest product releases and enhancements

Navigate the spatial world with engaging and informative content

NextBillion.ai vs. Google Route Optimization API

Experience a more powerful optimization and scheduling platform, better optimized routes, advanced integration capabilities and flexible pricing with NextBillion.ai.

API Documentation

Comprehensive API guides and references

Interactive API examples

Integrate tools you use to run your business

Technical Blogs

Deep-dive into the technical details

Get quick answers to common queries

FEATURED TECHNICAL BLOG

How to Implement Route Optimization API using Python

Learn how to implement route optimization for vehicle fleet management using python in this comprehensive tutorial.

ROUTE OPTIMIZATION API

API Reference

DISTANCE MATRIX API

Navigation api & sdk.

Android SDK

Flutter SDK

Documentation

Integration

NEXTBILLION.AI

Partner with us

Our story, vision and mission

Meet our tribe

Latest scoop on product updates, partnerships and more

Come join us - see open positions

Reach out to us for any product- or media-related queries

For support queries, write to us at

To partner with us, contact us at

For all media-related queries, reach out to us at

For all career-related queries, reach out to us at

Request a Demo

Table of Contents

9 Best Algorithms for Traveling Salesman Problem Solutions

Rishabh singh.

March 15, 2024

In the field of combinatorial optimization, the Traveling Salesman Problem (TSP) is a well-known puzzle with applications ranging from manufacturing and circuit design to logistics and transportation. The goal of cost-effectiveness and efficiency has made it necessary for businesses and industries to identify the best TSP solutions. It’s not just an academic issue, either. Using route optimization algorithms to find more profitable routes for delivery companies also lowers greenhouse gas emissions since fewer miles are traveled.

What is the Traveling Salesman Problem?

The TSP has captivated mathematicians, computer scientists, and operations researchers for decades. At its core, the problem is deceptively simple: given a list of cities and the distances between each pair, find the shortest possible route that visits each city once and then returns to the origin city. Despite its simplicity, the TSP is notoriously difficult to solve, especially as the number of cities increases.

In this technical blog, we’ll examine some top algorithms for Traveling Salesman Problem solutions and describe their advantages, disadvantages and practical uses.

Explore NextBillion.ai’s Route Optimization API , which uses advanced algorithms to solve TSP in real-world scenarios.

The Branch-and-Bound Method

The nearest neighbor method, ant colony optimization.

Genetic Algorithms

The Lin-Kernighan Heuristic

Chained lin-kernighan heuristic, the christofides algorithm, concorde tsp solver.

These algorithms represent a diverse toolkit of Traveling Salesman Problem solutions, each with its advantages and trade-offs. Understanding their mechanisms and applications can help select the right approach for specific instances and requirements, whether you seek exact solutions or efficient approximations. So, let’s take a closer look at these algorithms and how they work.

Brute Force Algorithm

The simplest method for solving the TSP is the brute force algorithm. It includes looking at every way the cities could be scheduled and figuring out how far away each approach is overall. Since it ensures that the best solution will be found, it is not useful for large-scale situations due to its time complexity, which increases equally with the number of cities.

This is a detailed explanation of how the TSP is solved by the brute force algorithm:

Create Every Permutation: Make every combination of the cities that is possible. There are a total of n! permutations to think about for n cities. Every combination shows a possible sequence where the salesman could visit the cities.

Determine the Total Distance for Every Combination: Add up the distances between each city in the permutation to find the overall distance traveled for each one. To finish the trip, consider the time from the final city to the starting point.

Determine the Best Option: Observe which permutation produces the smallest total distance and record it. This permutation represents the ideal tour. Return the most effective permutation to the TSP as the solution after examining every option.

Give back the best answer possible: Return the most effective permutation to the TSP as the solution after all possible combinations have been examined.

Even though this implementation gives an exact solution for the TSP, it becomes costly to compute for larger instances due to its time complexity, which increases factorially with the number of cities.

The Branch-and-Bound method can be used to solve the Traveling Salesman Problem (TSP) and other combinatorial optimization problems. To effectively find a suitable space and the best answer, divide-and-conquer strategies are combined with eliminating less-than-ideal solutions.

This is how the Branch and Bound method for the Traveling Salesman Problem works:

Start : First, give a simple answer. You could find this by starting with an empty tour or using a heuristic method.

Limit Calculation : Find the lowest total cost of the current partial solution. This limit shows the least amount of money needed to finish the tour.

Divide : Select a variable that is associated with the subsequent stage of the tour. This could mean picking out the next city to visit.

When making branches, think about the possible values for the variable you’ve chosen. Each branch stands for a different choice or option.

Cutting down : If a branch’s lower bound is higher than the best-known solution right now, cut it because you know that it can’t lead to the best solution.

Exploration : Keep using the branch-and-bound method to look into the other branches. Keep cutting and branching until all of your options have been thought through.

New Ideal Solution : Save the best solution you found while doing research. You should change the known one if a new, cheaper solution comes along.

Termination : Continue investigating until all possible paths have been considered and no more choices exist that could lead to a better solution. End the algorithm when all possible outcomes have been studied.

Selecting the order in which to visit the cities is one of the decision variables for the Traveling Salesman Problem. Usually, methods like the Held-Karp lower bound are used to calculate the lower bound. The technique identifies and cuts branches that are likely to result in less-than-ideal solutions as it carefully investigates various combinations of cities.

A heuristic algorithm called the Nearest Neighbor method estimates solutions to the Traveling Salesman Problem (TSP). In contrast to exact methods like brute force or dynamic programming, which always get the best results, the Nearest Neighbor method finds a quick and reasonable solution by making local, greedy choices.

Here is a detailed explanation of how the nearest-neighbor method solves the TSP problem:

Starting Point : Pick a city randomly to be the tour’s starting point.

Picking Something Greedy: Select the next city on the tour to visit at each stage based on how close the current city is to the not-explored city. Usually, a selected measurement is used to calculate the distance between cities (e.g., Euclidean distance).

Go and Mark: Visit the closest city you picked, add it to your tour, and mark it as observed.

Additionally: Continue this manner until every city has been visited at least once.

Go Back to the Beginning City: After visiting all the other cities, return to the starting city to finish the tour.

The nearest-neighbor method’s foundation is making locally optimal choices at each stage and hoping that the sum of these choices will produce a reasonable overall solution. Compared to exact algorithms, this greedy approach drastically lowers the level of computation required, which makes it appropriate for relatively large cases of the TSP.

ACO, or Ant Colony Optimization, is a metaheuristic algorithm that draws inspiration from ants’ seeking habits. It works very well for resolving a combination of optimization issues, such as the TSP (Traveling Salesman Problem). The idea behind ACO is to imitate ant colonies’ chemical trail communication to determine the best routes.

Ant Colony Optimization provides the following solution for the Traveling Salesman Problem:

Starting Point: A population of synthetic ants should be planted in a random starting city. Every ant is a possible solution for the TSP.

Initialization of The scents: Give each edge in the problem space (connections between cities) an initial amount of synthetic pheromone. The artificial ants communicate with one another via the fragrance.

Ant Motion: Each ant creates a tour by constantly selecting the next city to visit using a combination of fragrance levels and a heuristic function.

The quantity of fragrance on the edge that links the candidate city to the current city, as well as a heuristic measure that could be based on factors like distance between cities, impact the chances of selecting a specific city.

Ants mimic how real ants use chemical trails for communication by following paths with higher fragrance levels.

Update on Pheromones: The pheromone concentration on every edge is updated once every ant has finished traveling.

The update involves placing fragrances on the borders of the best tours and evaporating existing fragrances to copy the natural breakdown of chemical paths, which is intended to encourage the search for successful paths.

Repetition: For the fixed number of cycles or until a shift standard is satisfied, repeat the steps of ant movement, fragrance update, and tour construction.

Building Solution : After a few iterations, the artificial ants develop an answer, which is considered the algorithm’s outcome. This solution approximates the most efficient TSP tour.

Enhancement: To improve progress and solution quality, the process can be optimized by adjusting parameters like the influence of the heuristic function and the rate at which fragrances evaporate.

Ant Colony Optimization is excellent at solving TSP cases by using the ant population’s group ability. By striking a balance between exploration and exploitation, the algorithm can find potential paths and take advantage of success. It is a well-liked option in the heuristics field since it has been effectively used to solve various optimization issues.

Genetic Algorithm

Genetic Algorithms (GAs) are optimization algorithms derived from the concepts of genetics and natural selection. These algorithms imitate evolution to find predictions for complex problems, such as the Traveling Salesman Problem (TSP).

Here is how genetic algorithms resolve the TSP:

Starting Point: select a starting group of possible TSP solutions. Every possible tour that visits every city exactly once is represented by each solution.

Assessment: Examine each solution’s fitness within the population. Fitness is commonly defined in the TSP environment as the opposite of the total distance traveled. Tour length is a determining factor in fitness scores.

Choice: Choose people from the population to be the parents of the following generation. Each person’s fitness level determines the likelihood of selection. More fit solutions have a higher chance of being selected.

Transformation (Recombination): To produce offspring, perform crossover, or recombination, on pairs of chosen parents. To create new solutions, crossover entails sharing information between parent solutions.

Crossover can be applied in various ways for TSP, such as order crossover (OX) or partially mapped crossover (PMX), to guarantee that the resulting tours preserve the authenticity of city visits.

Change: Change some of the offspring solutions to introduce arbitrary changes. A mutation can involve flipping two cities or changing the order of a subset of cities.

Mutations add diversity to the population when discovering new regions of the solution space.

Substitute: Parents and children together make up the new generation of solutions that will replace the old ones. A portion of the top-performing solutions from the previous generation may be retained in the new generation as part of a privileged replacement process.

Finalization: For a predetermined number of generations or until a convergence criterion is satisfied, repeat the selection, crossover, mutation, and replacement processes.

Enhancement: Modify variables like population size, crossover rate, and mutation rate to maximize the algorithm’s capacity to identify excellent TSP solutions.

When it comes to optimizing combinations, genetic algorithms are exceptional at sifting through big solution spaces and identifying superior answers. Because of their capacity to duplicate natural evolution, they can adjust to the TSP’s structure and find almost ideal tours. GAs are an effective tool in the field of evolutionary computation because they have been successfully applied to a wide range of optimization problems.

The Lin-Kernighan Heuristic is a local search algorithm that iteratively improves a tour by performing a series of edge exchanges.

How the Lin-Kernighan Heuristic works as a Traveling Salesman Problem solution:

Initial Tour: It begins with an initial tour, which can be generated by any heuristic method, allowing it to start from a reasonable solution.

Edge Exchanges: The algorithm identifies pairs of edges in the tour that can be exchanged to reduce the total tour length. This local optimization step is crucial in refining the tour.

Move Selection: It performs the best exchange and updates the tour, ensuring continuous improvement.

Repetition: The process is repeated until no further improvements can be found, ensuring a thorough search of the local neighborhood.

The heuristic uses variable-depth searches, making it adaptive and efficient for large datasets, as it can adjust the search depth based on the problem’s complexity. This adaptability and focus on local optimizations enable the Lin-Kernighan Heuristic to effectively handle large instances of TSP, often producing near-optimal solutions with relatively low computational effort.

The Chained Lin-Kernighan (CLK) Heuristic is an advanced extension of the Lin-Kernighan heuristic, designed to further enhance solution quality and efficiency for large instances of the TSP.

Here’s how Chained Lin-Kernighan can be used as a Traveling Salesman Problem solution:

Initial Tour: Start with an initial tour generated by any heuristic method.

Lin-Kernighan Improvements: Apply the Lin-Kernighan heuristic to iteratively improve the tour by performing a series of edge exchanges until no further improvements can be found.

K-Opt Moves: Introduce more complex k-opt moves, where multiple edges are swapped simultaneously to escape local minima and explore a larger solution space.

Tour Perturbation: Perturb the current tour by making substantial changes, such as removing a segment and reinserting it elsewhere, to jump to a new region of the solution space.

Reapplication: Reapply the Lin-Kernighan heuristic to the perturbed tour to refine it further.

Chaining Process: Repeat the perturbation and reapplication steps, creating a chain of tours that explore different regions of the solution space.

Selection: Select the best tour found during the chaining process.

By combining Lin-Kernighan improvements with more complex k-opt moves and tour perturbations, CLK often finds near-optimal solutions. The chaining process helps escape local minima by exploring new regions of the solution space, leading to better solutions. This algorithm is highly effective for large TSP instances, maintaining efficiency while improving solution quality.

The Christofides Algorithm is a well-known approximation algorithm for Traveling Salesman Problem solutions that guarantee an output within 1.5 times the optimal tour length. It combines several techniques to produce high-quality solutions efficiently.

Here’s how Christofides Algorithm resolves the TSP:

Minimum Spanning Tree (MST): Construct a minimum spanning tree of the graph, connecting all vertices with the least total edge weight without forming any cycles.

Odd Degree Vertices: Identify all vertices in the MST that have an odd degree. The number of these vertices is always even.

Minimum Weight Matching: Find a minimum weight matching for the odd degree vertices. This step pairs the odd degree vertices with the least possible total edge weight, resulting in a perfect matching.

Eulerian Circuit: Combine the edges of the MST and the minimum weight matching to form a multigraph with an Eulerian circuit (a circuit that visits every edge exactly once).

Hamiltonian Circuit: Convert the Eulerian circuit to a Hamiltonian circuit by skipping repeated vertices, which results in a valid TSP tour.

The Christofides Algorithm guarantees a solution within 1.5 times the optimal tour length, which is a significant advantage in approximation algorithms. This algorithm is particularly valuable in scenarios where an exact solution is not necessary, but a near-optimal solution is acceptable within a guaranteed bound. Its balance between computational efficiency and solution quality makes it a robust choice for approximating Traveling Salesman Problem solutions.

The Christofides Algorithm is a well-known

The Concorde TSP Solver is widely regarded as the state-of-the-art exact algorithm for Traveling Salesman Problem solutions. It is notable for its ability to handle large and complex instances efficiently, combining multiple advanced techniques to find optimal solutions.

How Concorde TSP Solver resolves the TSP:

Cutting Planes: Concorde uses cutting-plane methods to solve the linear programming relaxation of the TSP. This involves finding hyperplanes (cuts) that progressively tighten the feasible region of the solution space, excluding infeasible solutions and honing in on the optimal tour.

Branch and Bound: The algorithm employs branch-and-bound techniques to systematically explore subsets of solutions. By branching on decision variables and bounding using the current best solution, it effectively prunes large portions of the solution space, reducing the number of tours that need to be examined.

Heuristics: Concorde incorporates various heuristic methods to generate initial feasible solutions and improve intermediate solutions. These heuristics, such as the Lin-Kernighan heuristic and others, provide high-quality starting points and guide the search process.

Cutting Plane Management: The solver manages a pool of cutting planes, dynamically adding and removing them as needed. This ensures that the algorithm remains efficient and can handle large-scale problems without being overwhelmed by the number of cuts.

Concorde’s blend of cutting-edge mathematical techniques and practical heuristics is designed to find exact solutions, meaning it guarantees the optimality of the tour. Despite the complexity of TSP, Concorde’s advanced techniques allow it to solve instances with thousands of cities within a reasonable timeframe, making it the go-to solver for benchmark testing and large-scale applications. Its ability to deliver exact solutions for large-scale problems cements its reputation as the leading TSP solver.

approximation algorithm for Traveling Salesman Problem solutions that guarantee an output within 1.5 times the optimal tour length. It combines several techniques to produce high-quality solutions efficiently.

The Traveling Salesman Problem (TSP) remains a fundamental challenge in optimization, with a wide array of algorithms offering diverse approaches to finding solutions. Understanding these algorithms provides valuable insights for tackling complex routing problems, advancing both theoretical research and practical applications in various fields.

If you’re looking for a solution to help optimize routing for your business, NextBillion.ai offers an advanced Route Optimization API that solves real-life TSP and VRP problems and can be easily integrated with your applications.

Book a demo today to see firsthand how it works!

It is not possible to solve the Traveling Salesman Problem with Dijkstra’s algorithm. Dijkstra’s algorithm, a single-source shortest path algorithm, finds the shortest possible route from a given source node to every other node in a weighted graph. In comparison, the Traveling Salesman Problem looks for the quickest route that stops in every city exactly once before returning to the starting point.

The term “traveling salesman” refers to a scenario where a salesperson visits different cities to sell goods or services. The goal of this problem is to find the shortest route that goes to each city once and returns to the starting point. It is a fundamental problem in algorithmic optimization to determine the best order of city trips and minimize travel time or distance.

“Route salesman” or just “sales representative” are other terms for a traveling salesman. These people go to various places to sell goods and services to customers. The traveling salesman, who determines the shortest route to visit multiple cities, is often referred to as a “touring agent” or simply as the “salesman” in the context of mathematical optimization.

The minimum distance a salesman needs to visit each city exactly once and then return to the starting city is known as the shortest distance in the Traveling Salesman Problem (TSP). It stands for the ideal tour duration that reduces the total travel distance. The goal of solving the TSP, an essential issue in combinatorial optimization, is finding the shortest distance.

Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

ENGINEERING
What's the point?
life cycles
engineering
data visualization
biogeochemistry
social science
computer science
epidemiology

11 Animated Algorithms for the Traveling Salesman Problem

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action.

TSP Algorithms and heuristics

Although we haven’t been able to quickly find optimal solutions to NP problems like the Traveling Salesman Problem, "good-enough" solutions to NP problems can be quickly found [1] .

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action. Researchers often use these methods as sub-routines for their own algorithms and heuristics. This is not an exhaustive list.

For ease of visual comparison we use Dantzig49 as the common TSP problem, in Euclidean space. Dantzig49 has 49 cities — one city in each contiguous US State, plus Washington DC.

1: Greedy Algorithm

A greedy algorithm is a general term for algorithms that try to add the lowest cost possible in each iteration, even if they result in sub-optimal combinations.

In this example, all possible edges are sorted by distance, shortest to longest. Then the shortest edge that will neither create a vertex with more than 2 edges, nor a cycle with less than the total number of cities is added. This is repeated until we have a cycle containing all of the cities.

Although all the heuristics here cannot guarantee an optimal solution, greedy algorithms are known to be especially sub-optimal for the TSP.

2: Nearest Neighbor

The nearest neighbor heuristic is another greedy algorithm, or what some may call naive. It starts at one city and connects with the closest unvisited city. It repeats until every city has been visited. It then returns to the starting city.

Karl Menger, who first defined the TSP, noted that nearest neighbor is a sub-optimal method:

"The rule that one first should go from the staring point to the closest point, then to the point closest to this, etc., in general does not yield the shortest route."

The time complexity of the nearest neighbor algorithm is O(n^2) . The number of computations required will not grow faster than n^2.

3: Nearest Insertion

Insertion algorithms add new points between existing points on a tour as it grows.

One implementation of Nearest Insertion begins with two cities. It then repeatedly finds the city not already in the tour that is closest to any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible. It stops when no more insertions remain.

The nearest insertion algorithm is O(n^2)

4: Cheapest Insertion

Like Nearest Insertion, Cheapest Insertion also begins with two cities. It then finds the city not already in the tour that when placed between two connected cities in the subtour will result in the shortest possible tour. It inserts the city between the two connected cities, and repeats until there are no more insertions left.

The cheapest insertion algorithm is O(n^2 log2(n))

5: Random Insertion

Random Insertion also begins with two cities. It then randomly selects a city not already in the tour and inserts it between two cities in the tour. Rinse, wash, repeat.

Time complexity: O(n^2)

6: Farthest Insertion

Unlike the other insertions, Farthest Insertion begins with a city and connects it with the city that is furthest from it.

It then repeatedly finds the city not already in the tour that is furthest from any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible.

7: Christofides Algorithm

Christofides algorithm is a heuristic with a 3/2 approximation guarantee. In the worst case the tour is no longer than 3/2 the length of the optimum tour.

Due to its speed and 3/2 approximation guarantee, Christofides algorithm is often used to construct an upper bound, as an initial tour which will be further optimized using tour improvement heuristics, or as an upper bound to help limit the search space for branch and cut techniques used in search of the optimal route.

For it to work, it requires distances between cities to be symmetric and obey the triangle inequality, which is what you'll find in a typical x,y coordinate plane (metric space). Published in 1976, it continues to hold the record for the best approximation ratio for metric space.

The algorithm is intricate [2] . Its time complexity is O(n^4)

A problem is called k-Optimal if we cannot improve the tour by switching k edges.

Each k-Opt iteration takes O(n^k) time.

2-Opt is a local search tour improvement algorithm proposed by Croes in 1958 [3] . It originates from the idea that tours with edges that cross over aren’t optimal. 2-opt will consider every possible 2-edge swap, swapping 2 edges when it results in an improved tour.

2-opt takes O(n^2) time per iteration.

3-opt is a generalization of 2-opt, where 3 edges are swapped at a time. When 3 edges are removed, there are 7 different ways of reconnecting them, so they're all considered.

The time complexity of 3-opt is O(n^3) for every 3-opt iteration.

10: Lin-Kernighan Heuristic

Lin-Kernighan is an optimized k-Opt tour-improvement heuristic. It takes a tour and tries to improve it.

By allowing some of the intermediate tours to be more costly than the initial tour, Lin-Kernighan can go well beyond the point where a simple 2-Opt would terminate [4] .

Implementations of the Lin-Kernighan heuristic such as Keld Helsgaun's LKH may use "walk" sequences of 2-Opt, 3-Opt, 4-Opt, 5-Opt, “kicks” to escape local minima, sensitivity analysis to direct and restrict the search, as well as other methods.

LKH has 2 versions; the original and LKH-2 released later. Although it's a heuristic and not an exact algorithm, it frequently produces optimal solutions. It has converged upon the optimum route of every tour with a known optimum length. At one point in time or another it has also set records for every problem with unknown optimums, such as the World TSP, which has 1,900,000 locations.

11: Chained Lin-Kernighan

Chained Lin-Kernighan is a tour improvement method built on top of the Lin-Kernighan heuristic:

Lawrence Weru

Larry is a TEDx speaker, Harvard Medical School Dean's Scholar, Florida State University "Notable Nole," and has served as an invited speaker at Harvard, FSU, and USF. Larry's contributions are featured by Harvard University, Fast Company, and Gizmodo Japan, and cited in books by Routledge and No Starch Press. His stories and opinions are published in Slate, Vox, Toronto Star, Orlando Sentinel, and Vancouver Sun, among others. He illustrates the sciences for a more just and sustainable world.

2020 Presidential Election County Level Muddy Map Paid Members Public

2020 US Presidential Election Interactive County-Level Vote Map

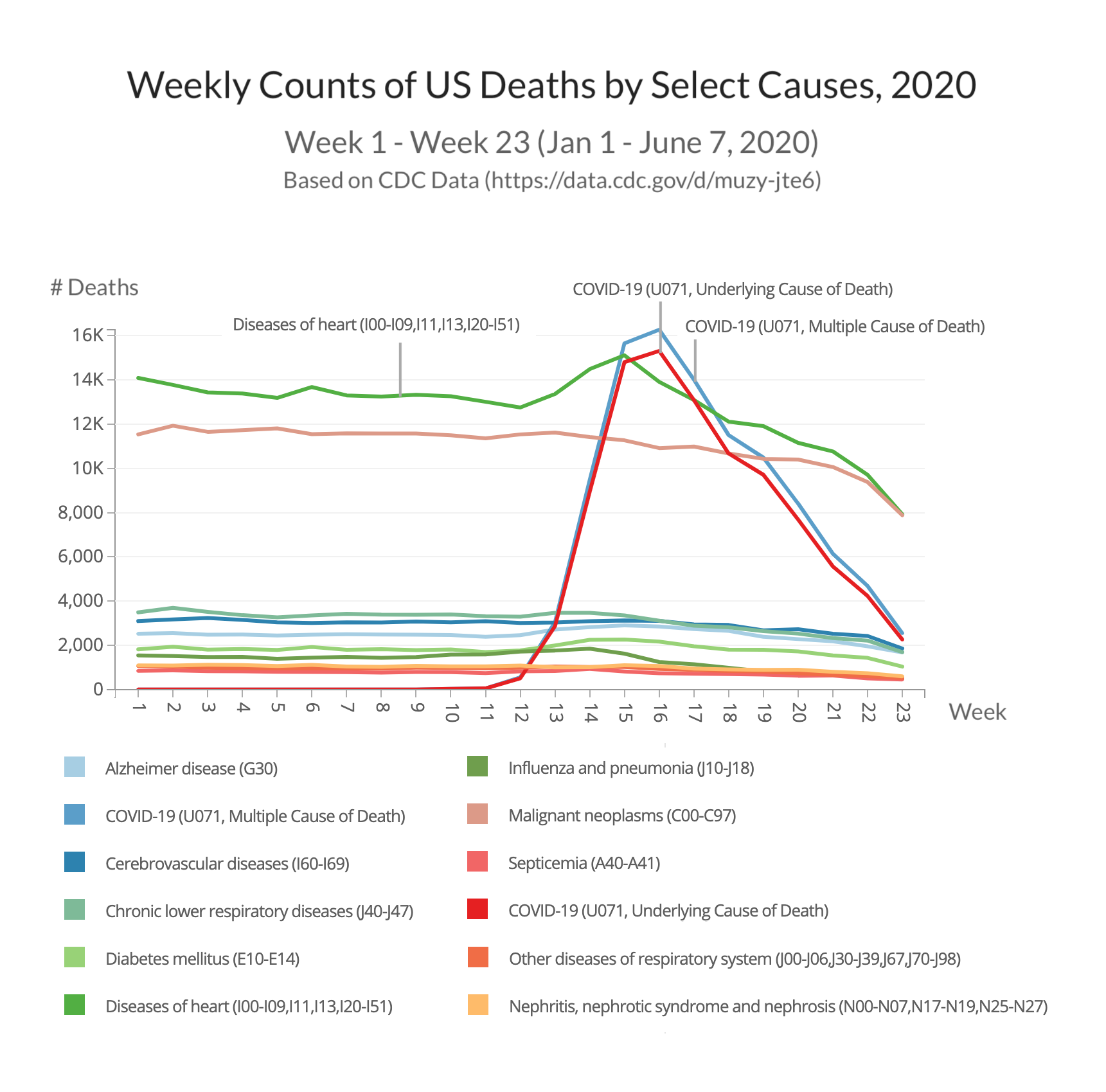
Weekly Counts of US Deaths by Select Causes through June 2020 Paid Members Public

This graph uses CDC data to compare COVID deaths with other causes of deaths.

STEM Lounge Newsletter

Be the first to receive the latest updates in your inbox.

Featured Posts

Tokyo olympics college medal count 🏅.

Muddy America : Color Balancing The US Election Map - Infographic

The trouble with the purple election map.

This website uses cookies to ensure you get the best experience on our website. You may opt out by using any cookie-blocking technology, such as your browser add-on of choice. Got it!

Traveling Salesman Algorithms

From naive to christofide, how to read this article.

Our article was written using a component-based library called Idyll. In addition to buttons and sliders you will see the following in this article... This component is an external link which will redirect you to another page. This component is an internal link which will send you to a part of the page when clicked on. This component is an action link which will trigger some event on the page to do something. Lastly, this article is only supported on Chrome; other browsers have an SVG rendering bug that can show up.

Introduction

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

In essence, this question is asking us (the salesman) to visit each of the cities via the shortest path that gets us back to our origin city. We can conceptualize the TSP as a graph where each city is a node, each node has an edge to every other node, and each edge weight is the distance between those two nodes.

The first computer coded solution of TSP by Dantzig, Fulkerson, and Johnson came in the mid 1950’s with a total of 49 cities. Since then, there have been many algorithmic iterations and 50 years later, the TSP problem has been successfully solved with a node size of 24,978 cities! Multiple variations on the problem have been developed as well, such as mTSP , a generalized version of the problem and Metric TSP , a subcase of the problem.

The original Traveling Salesman Problem is one of the fundamental problems in the study of combinatorial optimization—or in plain English: finding the best solution to a problem from a finite set of possible solutions . This field has become especially important in terms of computer science, as it incorporate key principles ranging from searching, to sorting, to graph theory.

Real World Applications

However, before we dive into the nitty gritty details of TSP, we would like to present some real-world examples of the problem to illustrate its importance and underlying concepts. Applications of the TSP include:

Click on an example to the left for more information!

Santa delivering presents.
Fulfilling an order in a warehouse.
Designing and building printed circuit boards.
Analyzing an X-Ray.
GPS satellite systems.
School bus scheduling.

Finding Solutions – Exact vs. Approximation

The difficulty in solving a combinatorial optimization problem such as the TSP lies not in discovering a single solution, but rather quickly verifying that a given solution is the optimal solution. To verify, without a shadow of a doubt, that a single solution is optimized requires both computing all the possible solutions and then comparing your solution to each of them. We will call this solution the Exact solution. The number of computations required to calculate this Exact solution grows at an enormous rate as the number of cities grow as well. For example, the total number of possible paths for 7 cities is just over 5,000 , for 10 cities it is over 3.6 million , and for 13 cities it is over 6 billion . Clearly, this growth rate quickly eclipses the capabilities of modern personal computers and determining an exact solution may be near impossible for a dataset with even 20 cities. We will explore the exact solution approach in greater detail during the Naïve section.

The physical limitations of finding an exact solution lead us towards a very important concept – approximation algorithms . In an approximation algorithm, we cannot guarantee that the solution is the optimal one, but we can guarantee that it falls within a certain proportion of the optimal solution. The real strength of approximation algorithms is their ability to compute this bounded solution in an amount of time that is several orders of magnitude quicker than the exact solution approach. Later on in this article we will explore two different approximation algorithms, Nearest Neighbor and Christofide’s Algorithm , and the many facets of each approach.

The Naïve Approach

We can imagine that from a starting city, there are ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 possibilities for the second city. Following this connection, the second city will then have ∣ V ∣ − 2 |V| - 2 ∣ V ∣ − 2 possibilities, and so on and so on... Since our path is bidirectional, it follows that some cycles we calculate at will be disposible as they are duplicates if reversed. Thus we arrive at ( ∣ V ∣ − 1 ) ! / 2 (|V| - 1)!/2 ( ∣ V ∣ − 1 ) ! / 2 possible paths.

This figure can better be expressed as having a bound O ( ∣ V ∣ ! ) O(|V|!) O ( ∣ V ∣ ! ) possible paths. As explored above, a factorial upper bound is simply far too great for real applications.

Nearest Neighbor

Choose the next city in the path to be the closest city that you have not already visited. Once all cities have been visited, the salesman return home.

Next: Click here for a quick walkthrough of the algorithm!

Christofides Algorithm

Steps: Intro MST Odd Vertices Matches Eulerian Hamiltonian

This section is meant to serve as a “slide show” that will walk you through the previously outlined 5 steps of Christofides’ Algorithm. At each step after this one you will be able to switch between a Small Dataset , Medium Dataset , and Large Dataset , Clear the edges in the graph, and move to the previous step and Next Step in the algorithm.

In addition, each step can be accessed by clicking its corresponding button underneath the map to the right. Next Step: Minimum Spanning Tree

Algorithm Analysis

While the Naïve and dynamic programming approaches always calculate the exact solution, it comes at the cost of enormous runtime; datasets beyond 15 vertices are too large for personal computers. The most common approximation algorithm, Nearest Neighbor, can produce a very good result (within 25% of the exact solution) for most cases, however it has no guarantee on its error bound. That said, Christofides algorithm has the current best error bound of within 50% of the exact solution for approximation algorithms. Christofides produces this result in a “good” runtime compared to Naïve and dynamic, but it still significantly slower than the Nearest Neighbor approach.

In the chart above the runtimes of the naive, dynamic programming, nearest neighbors, and Christofides’ are plotted. The x-axis represents the number of cities that the algorithm works on while the y-axis represents the worst-case amount of calculations it will need to make to get a solution. As you can see, as the number of cities increases every algorithm has to do more calculations however naive will end up doing significantly more. Note how with 20 cities, the naive algorithm is 5,800,490,399 times slower than even the minimally faster dynamic programming algorithm.

Closing Thoughts

We would like to thank Dr. Heer, Matthew Conlen, Younghoon Kim, and Kaitlyn Zhou for their contributions to CSE 442, the UW Interactive Data Lab, Idyll, and much more. This article would not have been possible without their support and guidance.

Sources, References, and Links:

Inspiration from Idyll articles: Flight, Barnes Hut

Traveling Salesman Problem

The traveling salesman problem (TSP) asks the question, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?".

This project

The goal of this site is to be an educational resource to help visualize, learn, and develop different algorithms for the traveling salesman problem in a way that's easily accessible
As you apply different algorithms, the current best path is saved and used as input to whatever you run next. (e.g. shortest path first -> branch and bound). The order in which you apply different algorithms to the problem is sometimes referred to the meta-heuristic strategy.

Heuristic algorithms

Heuristic algorithms attempt to find a good approximation of the optimal path within a more reasonable amount of time.

Construction - Build a path (e.g. shortest path)

Shortest Path

Arbitrary Insertion

Furthest insertion.

Nearest Insertion
Convex Hull Insertion*
Simulated Annealing*

Improvement - Attempt to take an existing constructed path and improve on it

2-Opt Inversion
2-Opt Reciprcal Exchange*

Exhaustive algorithms

Exhaustive algorithms will always find the best possible solution by evaluating every possible path. These algorithms are typically significantly more expensive then the heuristic algorithms discussed next. The exhaustive algorithms implemented so far include:

Random Paths

Depth First Search (Brute Force)

Branch and Bound (Cost)
Branch and Bound (Cost, Intersections)*

Dependencies

These are the main tools used to build this site:

web workers
material-ui

Contributing

Pull requests are always welcome! Also, feel free to raise any ideas, suggestions, or bugs as an issue.

This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example,

With 10 points there are 181,400 paths to evaluate.
With 11 points, there are 1,814,000.
With 12 points there are 19,960,000.
With 20 points there are 60,820,000,000,000,000, give or take.
With 25 points there are 310,200,000,000,000,000,000,000, give or take.

This is factorial growth, and it quickly makes the TSP impractical to brute force. That is why heuristics exist to give a good approximation of the best path, but it is very difficult to determine without a doubt what the best path is for a reasonably sized traveling salesman problem.

This is a recursive, depth-first-search algorithm, as follows:

From the starting point
For all other points not visited
If there are no points left return the current cost/path
Else, go to every remaining point and
Mark that point as visited
" recurse " through those paths (go back to 1. )

Implementation

Nearest neighbor.

This is a heuristic, greedy algorithm also known as nearest neighbor. It continually chooses the best looking option from the current state.

sort the remaining available points based on cost (distance)
Choose the closest point and go there
Chosen point is no longer an "available point"
Continue this way until there are no available points, and then return to the start.

Two-Opt inversion

This algorithm is also known as 2-opt, 2-opt mutation, and cross-aversion. The general goal is to find places where the path crosses over itself, and then "undo" that crossing. It repeats until there are no crossings. A characteristic of this algorithm is that afterwards the path is guaranteed to have no crossings.

While a better path has not been found.
For each pair of points:
Reverse the path between the selected points.
If the new path is cheaper (shorter), keep it and continue searching. Remember that we found a better path.
If not, revert the path and continue searching.

This is a heuristic construction algorithm. It select a random point, and then figures out where the best place to put it will be.

First, go to the closest point
Choose a random point to go to
Find the cheapest place to add it in the path
Continue from #3 until there are no available points, and then return to the start.

This is an impractical, albeit exhaustive algorithm. It is here only for demonstration purposes, but will not find a reasonable path for traveling salesman problems above 7 or 8 points.

I consider it exhaustive because if it runs for infinity, eventually it will encounter every possible path.

From the starting path
Randomly shuffle the path
If it's better, keep it
If not, ditch it and keep going

Two-Opt Reciprocal Exchange

This algorithm is similar to the 2-opt mutation or inversion algorithm, although generally will find a less optimal path. However, the computational cost of calculating new solutions is less intensive.

The big difference with 2-opt mutation is not reversing the path between the 2 points. This algorithm is not always going to find a path that doesn't cross itself.

It could be worthwhile to try this algorithm prior to 2-opt inversion because of the cheaper cost of calculation, but probably not.

Swap the points in the path. That is, go to point B before point A, continue along the same path, and go to point A where point B was.

Branch and Bound on Cost

This is a recursive algorithm, similar to depth first search, that is guaranteed to find the optimal solution.

The candidate solution space is generated by systematically traversing possible paths, and discarding large subsets of fruitless candidates by comparing the current solution to an upper and lower bound. In this case, the upper bound is the best path found so far.

While evaluating paths, if at any point the current solution is already more expensive (longer) than the best complete path discovered, there is no point continuing.

For example, imagine:

A -> B -> C -> D -> E -> A was already found with a cost of 100.
We are evaluating A -> C -> E, which has a cost of 110. There is no point evaluating the remaining solutions.

Instead of continuing to evaluate all of the child solutions from here, we can go down a different path, eliminating candidates not worth evaluating:

A -> C -> E -> D -> B -> A
A -> C -> E -> B -> D -> A

Implementation is very similar to depth first search, with the exception that we cut paths that are already longer than the current best.

This is a heuristic construction algorithm. It selects the closest point to the path, and then figures out where the best place to put it will be.

Choose the point that is nearest to the current path

Branch and Bound (Cost, Intersections)

This is the same as branch and bound on cost, with an additional heuristic added to further minimize the search space.

While traversing paths, if at any point the path intersects (crosses over) itself, than backtrack and try the next way. It's been proven that an optimal path will never contain crossings.

Implementation is almost identical to branch and bound on cost only, with the added heuristic below:

This is a heuristic construction algorithm. It selects the furthest point from the path, and then figures out where the best place to put it will be.

Choose the point that is furthest from any of the points on the path

Convex Hull

This is a heuristic construction algorithm. It starts by building the convex hull , and adding interior points from there. This implmentation uses another heuristic for insertion based on the ratio of the cost of adding the new point to the overall length of the segment, however any insertion algorithm could be applied after building the hull.

There are a number of algorithms to determine the convex hull. This implementation uses the gift wrapping algorithm .

In essence, the steps are:

Determine the leftmost point
Continually add the most counterclockwise point until the convex hull is formed
For each remaining point p, find the segment i => j in the hull that minimizes cost(i -> p) + cost(p -> j) - cost(i -> j)
Of those, choose p that minimizes cost(i -> p -> j) / cost(i -> j)
Add p to the path between i and j
Repeat from #3 until there are no remaining points

Simulated Annealing

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.

For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms

Visualize algorithms for the traveling salesman problem. Use the controls below to plot points, choose an algorithm, and control execution. (Hint: try a construction alogorithm followed by an improvement algorithm)

Interview Problems on Graph
Practice Graph
MCQs on Graph
Graph Tutorial
Graph Representation
Graph Properties
Types of Graphs
Graph Applications
BFS on Graph
DFS on Graph
Graph VS Tree
Transpose Graph
Dijkstra's Algorithm
Minimum Spanning Tree
Prim’s Algorithm
Topological Sorting
Floyd Warshall Algorithm
Strongly Connected Components
Advantages & Disadvantages

Traveling Salesman Problem using Genetic Algorithm

AuPrerequisites: Genetic Algorithm , Travelling Salesman Problem In this article, a genetic algorithm is proposed to solve the travelling salesman problem . Genetic algorithms are heuristic search algorithms inspired by the process that supports the evolution of life. The algorithm is designed to replicate the natural selection process to carry generation, i.e. survival of the fittest of beings. Standard genetic algorithms are divided into five phases which are:

Creating initial population.
Calculating fitness.
Selecting the best genes.
Crossing over.
Mutating to introduce variations.

These algorithms can be implemented to find a solution to the optimization problems of various types. One such problem is the Traveling Salesman Problem . The problem says that a salesman is given a set of cities, he has to find the shortest route to as to visit each city exactly once and return to the starting city. Approach: In the following implementation, cities are taken as genes, string generated using these characters is called a chromosome, while a fitness score which is equal to the path length of all the cities mentioned, is used to target a population. Fitness Score is defined as the length of the path described by the gene. Lesser the path length fitter is the gene. The fittest of all the genes in the gene pool survive the population test and move to the next iteration. The number of iterations depends upon the value of a cooling variable. The value of the cooling variable keeps on decreasing with each iteration and reaches a threshold after a certain number of iterations. Algorithm:

Pseudo-code

How the mutation works? Suppose there are 5 cities: 0, 1, 2, 3, 4. The salesman is in city 0 and he has to find the shortest route to travel through all the cities back to the city 0. A chromosome representing the path chosen can be represented as:

This chromosome undergoes mutation. During mutation, the position of two cities in the chromosome is swapped to form a new configuration, except the first and the last cell, as they represent the start and endpoint.

Original chromosome had a path length equal to INT_MAX , according to the input defined below, since the path between city 1 and city 4 didn’t exist. After mutation, the new child formed has a path length equal to 21 , which is a much-optimized answer than the original assumption. This is how the genetic algorithm optimizes solutions to hard problems.

Below is the implementation of the above approach:

Time complexity: O(n^2) as it uses nested loops to calculate the fitness value of each gnome in the population. Auxiliary Space : O(n)

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

Solving Travelling Salesman (TSP) Using 2-Opt Algorithm in Python
Solving Traveling Salesman Problem through Optimization Techniques
Approximation Algorithm for Travelling Salesman Problem (2023)
Travelling Salesman Problem (TSP) Algorithm Implementation
Information
Travelling Salesman Problem

VIDEO

Travelling Salesman Problem
travelling salesman problem || brute force algorithm || graph theory || SEC || 4 yrs math honours
Traveling Salesmen Problem using ACO , GA, NN Algorithm
Genetic algorithm & Travelling salesman problem (IT)
Traveling Salesman Problem
Travelling Salesman Problem using Branch and Bound Method|| Solved Example|| Easy Tips

COMMENTS

Travelling salesman problem
Travelling salesman problem
Traveling Salesman Problem (TSP) Implementation
Traveling Salesman Problem (TSP) Implementation
DSA The Traveling Salesman Problem
DSA The Traveling Salesman Problem
Travelling Salesman Problem using Dynamic Programming
Travelling Salesman Problem using Dynamic Programming
Travelling Salesman Problem: Python, C++ Algorithm
Algorithm for Traveling Salesman Problem. We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP). Before starting the algorithm, let's get acquainted with some terminologies: A graph G= (V, E), which is a set of vertices and edges. V is the set of vertices. E is the set of edges.
Travelling Salesman Problem (Greedy Approach)
Travelling Salesman Problem (Greedy Approach)
Travelling salesman problem explained
Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms Defining the Travelling Salesman Problem: A Comprehensive Overview. The Travelling Salesman Problem, often abbreviated as TSP, has a strong footing in the realm of computer science. To the untrained eye, it presents itself as a puzzle: a salesperson or traveling ...
Traveling Salesman Problem: Exact Solutions vs. Heuristic vs ...
Traveling Salesman Problem: Exact Solutions vs. Heuristic ...
Travelling Salesman Problem: Definition, Algorithms & Solutions
Three Common Algorithms for the Traveling Salesman Problem 1. Brute-Force Method. The brute-force method, sometimes called the naive approach, tries every possible route to find the shortest one. To use this method, you list all possible routes, calculate the distance for each one, and then pick the shortest route as the best solution. ...
PDF Approximation Algorithms: Traveling Salesman Problem
3.1 Approximation Ratio. We will show that the Christofies algorithm is a 3 -approximation algorithm for the metric TSP. 2. problem. We first note that an Euler tour of T / = T ∪ M exists because all vertices are of even degree. We now bound the cost of the matching M. Lemma 3 c(M) ≤ 1 c(H∗). 2.
Algorithms for the Travelling Salesman Problem
Algorithms for the Travelling Salesman Problem
Best Algorithms for the Traveling Salesman Problem
Best Algorithms for the Traveling Salesman Problem
Travelling Salesman Problem
Travelling Salesman Problem
11 Animated Algorithms for the Traveling Salesman Problem
11 Animated Algorithms for the Traveling Salesman Problem
Traveling salesman problem
problem. traveling salesman problem, an optimization problem in graph theory in which the nodes (cities) of a graph are connected by directed edges (routes), where the weight of an edge indicates the distance between two cities. The problem is to find a path that visits each city once, returns to the starting city, and minimizes the distance ...
How to Solve Traveling Salesman Problem
The traveling salesman problem is a classic problem in combinatorial optimization. This problem is finding the shortest path a salesman should take to traverse a list of cities and return to the origin city. ... The 2-opt algorithm is a simple local search method with a special swapping mechanism that works as its heuristic. The main idea ...
Traveling Salesman Algorithms
The original Traveling Salesman Problem is one of the fundamental problems in the study of combinatorial optimization—or in plain English: finding the best solution to a problem from a finite set of possible solutions. This field has become especially important in terms of computer science, as it incorporate key principles ranging from ...
Heuristic Algorithms for the Traveling Salesman Problem
Heuristic Algorithms for the Traveling Salesman Problem
Convex Hull
This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example, With 10 points there are 181,400 paths to evaluate. With 20 points there are 60,820,000,000,000,000, give or take.
6.6: Hamiltonian Circuits and the Traveling Salesman Problem
Hamiltonian Circuits and the Traveling Salesman Problem
How To Solve Travelling Salesman Problem With Simulated Annealing
The bottom plot shows the route of the best solution we found through the SA algorithm. From a simple 'eye-test' this new solution is much better than the initial and seems to be quite optimal. Summary. In this post we have gone over the travelling salesman problem, which asks us to find the shortest route for a set of cities (points).
Traveling Salesman Problem using Genetic Algorithm
Traveling Salesman Problem using Genetic Algorithm

DSA Tutorial

Checking All Routes to Solve The Traveling Salesman Problem

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

Time Complexity for Solving The Traveling Salesman Problem

Actual Traveling Salesman Problems Are More Complex

COLOR PICKER

Contact Sales

Report Error

Top Tutorials

Travelling Salesman Problem (Greedy Approach)

Travelling salesman problem explained

Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms

Unraveling TSP Algorithms: From Brute Force to Heuristics

Delivery notifications and tracking improve customer satisfaction by 27%.

Practical Solutions to the Travelling Salesman Problem

Practical code implementation

Optimizing TSP Solutions: Tips and Tricks

Expert Advice for Maximum Efficiency Minimum Cost

Real-World Applications of the Travelling Salesman Problem

Real-World Examples

TSP in GIS and Urban Planning: Optimal Route

Delving Deeper: The Complexity and History of the Travelling Salesman Problem

Unravel the Intricacies: Why is TSP complex?

NP-hard and TSP: A Connection Explored

A Look Back: The History of the Travelling Salesman Problem

The Origins and Evolution of TSP

Milestones in TSP Research

Wrapping Up The Journey With Algorithms and Solutions

Grow with confidence

Want to access our large pool of drivers?

Travelling Salesman Problem: Definition, Algorithms & Solutions

Table Of Contents

Three Common Algorithms for the Traveling Salesman Problem

1. Brute-Force Method

2. Branch and Bound Method

3. Nearest Neighbor Method

What is a Hamiltonian cycle, and why is it key to the Travelling Salesman Problem?

How does linear programming help with the Travelling Salesman Problem?

What is recursion, and how does it apply to the Travelling Salesman Problem?

Why is time complexity important for understanding the Travelling Salesman Problem?

Similar posts

How to Boost Profitability and Efficiency with a Sales Route Planner

Distribution Center Processes and Best Practices You Need to Know

The leading Route Optimization resource

Algorithms for the Travelling Salesman Problem

Three popular Travelling Salesman Problem Algorithms

1. The brute-force approach

2. The branch and bound method

3. The nearest neighbor method

How route optimization algorithms work to solve the Travelling Salesman Problem.

Real-world TSP applications

Real-life TSP and VRP solvers

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Frequently Asked Questions

What role does linear programming play in solving the Travelling Salesman Problem?

What is recursion, and how does it apply to the Travelling Salesman Problem?

Related articles

Solving the Vehicle Routing Problem (2024)

How To Optimize Multi-Stop Routes With Google Maps (2024)

How Route Optimization Impacts Our Earth

Key Products

Supply Chain & Logistics

Field Workforce

BY BUSINESS TYPE

BY LOGISTICS TYPE

NextBillion.ai vs. Google Route Optimization API

FEATURED TECHNICAL BLOG

How to Implement Route Optimization API using Python

ROUTE OPTIMIZATION API

DISTANCE MATRIX API

NEXTBILLION.AI

9 Best Algorithms for Traveling Salesman Problem Solutions

What is the Traveling Salesman Problem?

Popular Traveling Salesman Problem Solution Algorithms

The Branch-and-Bound Method

The Lin-Kernighan Heuristic

Brute Force Algorithm

Genetic Algorithm

In this Article