radio waves travel faster than sound waves give reason

Home » Science » Physics » Difference Between Radio Waves and Sound Waves

Difference Between Radio Waves and Sound Waves

Main difference – radio waves vs. sound waves.

Sounds are made of waves and radios produce sound. However, when we talk about radio waves , we are not talking about the sound waves produced by the radio. Rather, we are talking about the waves that transmit radio signals. The main difference between radio waves and sound waves is that radio waves are a type of electromagnetic wave that can travel when there is no medium , whereas sound waves are a type of mechanical wave that cannot travel if there is no medium .

What are Radio Waves

Radio waves are electromagnetic waves . These are waves composed of electric and magnetic fields , which are oscillating at right angles to each other. The energy of an electromagnetic wave propagates at a direction at right angles to the oscillations in both the electric and magnetic fields. In the diagram below, the black arrows show the oscillations in electric and magnetic fields. The direction of propagation of the wave is indicated by the grey arrow.

Difference Between Radio Waves and Sound Waves - Electromagnetic_Waves

Oscillations in an electromagnetic wave.

Since the actual oscillations take place at right angles to the direction of wave propagation, radio waves are transverse waves . Since radio waves are not mechanical, they do not need a medium to travel in; they can travel even in a vacuum. Like all types of electromagnetic waves, radio waves travel at a speed of about 300 000 km per second in a vacuum. When radio waves enter into other material, they slow down a little.

When you tune a radio to listen to a particular frequency, the radio takes in the signals at that frequency. Then, the radio’s circuits convert the electric signals into the movements in the speaker. These movements create movements in the air in front of the speaker, recreating the sound.

Difference Between Radio Waves and Sound Waves - Old_Radio

An old radio

What are Sound Waves

Sound waves are mechanical longitudinal waves . “Mechanical” means that sound waves must have a medium to pass through. The sound is really composed of the back-and-forth motion of molecules that make up the medium. These back-and-forth motions of molecules cause them to come towards each other, forming compressions . Then, the molecules move away from each other, forming rarefactions . This happens over and over again. Humans can “hear” sounds when a molecule undergoes this back-and-forth motion about 20-20 000 times per second. We say that sound waves are “longitudinal” because the movement of molecules take place parallel to the direction that the sound travels in. The speed of sound in a medium depends on the density of the material. Sound travels through air at room temperature and pressure at a speed of about 340 m per second. Typically, sound can travel faster in liquids and even faster in solids. Sound can travel through diamond at a speed of about 12 km per second 1 .

Difference Between Radio Waves and Sound Waves - Sound_Waves

Sound is really a pressure wave , composed of compressions and rarefactions in the molecules that make up the medium.

Radio waves are electromagnetic waves that can travel through a vacuum.

Sound waves are mechanical waves that require a medium to travel through.

Wave classification

Radio waves are transverse waves. They can be polarised.

Sound waves are longitudinal waves. They cannot be polarised.

Radio waves are much faster, typically travelling millions of metres per second.

Sound waves are much slower, typically travelling a few hundred or a few thousand metres per second.

1 . Nave, R. (2012). Speed of Sound . Retrieved September 17, 2015, from HyperPhysics Concepts

Image Courtesy

“Electromagnetic wave” by User:LennyWikidata (Own work) [ CC BY-SA 3.0 ], via Wikimedia Commons

“Dad’s Radio” by PROAlan Levine (Own work) [ CC BY 2.0 ], via flickr

“Diagram showing physical manifestation of a sound wave through air from a speaker to a human ear” by Pluke (Own work) [ CC0 1.0 ], via Wikimedia Commons (modified)

About the Author: Nipun

5.1.1: Speeds of Different Types of Waves

Last updated
Save as PDF
Page ID 26167

Kyle Forinash and Wolfgang Christian

The speed of a wave is fixed by the type of wave and the physical properties of the medium in which it travels. An exception is electromagnetic waves which can travel through a vacuum. For most substances the material will vibrate obeying a Hooke's law force as a wave passes through it and the speed will not depend on frequency. Electromagnetic waves in a vacuum and waves traveling though a linear medium are termed linear waves and have constant speed. Examples:

For sound waves in a fluid (for example air or water) the speed is determined by \(v=(B/\rho )^{1/2}\) where \(B\) is the bulk modulus or compressibility of the fluid in newtons per meter squared and \(\rho\) is the density in kilograms per cubic meter.
For sound waves in a solid the speed is determined by \(v= (Y/\rho )^{1/2}\) where \(Y\) is Young's modulus or stiffness in Newtons per meter squared and \(\rho\) is the density in kilograms per meter cubed.
For waves on a string the speed is determined by \(v=(T/\mu )^{1/2}\) where \(T\) is the tension in the string in Newtons and \(\mu\) is the mass per length in kilograms per meter.
Although electromagnetic waves do not need a medium to travel (they can travel through a vacuum) their speed in a vacuum, \(c = (1/\mu _{o} ε_{o})^{1/2} = 3.0\times 10^{8}\text{ m/s}\) is governed by two physical constants, the permeability \(\mu_{o}\) and the permittivity, \(ε_{o}\) of free space (vacuum).

Table \(\PageIndex{1}\)

Here is a more comprehensive list of the speed of sound in various materials .

As we saw in the previous chapter, there is a relationship between the period, wavelength and speed of the wave. The period of a cork floating in the water is affected by how fast the wave passes (wave speed) and the distance between peaks (wavelength). The relationship between speed, period and wavelength of a sine wave is given by \(v=\lambda /T\) where wavelength and period for a sine wave were defined previously. This can also be written as \(v=\lambda f\) since frequency is the inverse of period and is true for all linear waves. Notice that, since wave speed is normally a fixed quantity the frequency and wavelength will be inversely proportion; higher frequencies mean shorter wavelengths.

Often it is easier to write \(ω = 2πf\) where \(\omega\) is the angular frequency in radians per second instead of having to write \(2\pi f\) everywhere. Likewise it is easier to write \(k=2\pi /\lambda \) where \(k\) is the wave number in radians per meter rather than having to write \(2\pi /\lambda\) a lot. (Note that \(k\) is not a spring constant here.) Using these new definitions the speed of a wave can also be written as \(v=f\lambda =\omega /k\).

If the medium is uniform the speed of a wave is fixed and does not change. There are circumstances where the speed of a particular wave does change, however. Notice that the speed of sound in air depends on the density of the air (mass per volume). But the density of air changes with temperature and humidity. So the speed of sound can be different on different days and in different locations. The temperature dependence of the speed of sound in air is given by \(v = 344 + 0.6 (T - 20)\) in meters per second where \(T\) is the temperature in Celsius (\(T\) here is temperature, not period). Notice that at room temperature (\(20^{\circ}\text{C}\)) sound travels at \(344\text{ m/s}\).

The speed of sound can also be affected by the movement of the medium in which it travels. For example, wind can carry sound waves further (i.e. faster) if the sound is traveling in the same direction or it can slow the sound down if the sound is traveling in a direction opposite to the wind direction.

Electromagnetic waves travel at \(\text{c} = 3.0\times 10^{8}\text{ m/s}\) in a vacuum but slow down when they pass through a medium (for example light passing from air to glass). This occurs because the material has a different value for the permittivity and/or permeability due to the interaction of the wave with the atoms of the material. The amount the speed changes is given by the index of refraction \(n=c/v\) where \(c\) is the speed of light in a vacuum and \(v\) is the speed in the medium. The frequency of the wave does not change when it slows down so, since \(v=\lambda f\), the wavelength of electromagnetic waves in a medium must be slightly smaller.

Video/audio examples:

What is the speed of sound in a vacuum? Buzzer in a bell jar . Why is there no sound when the air is removed from the jar?
Demonstration of speed of sound in different gasses . Why is there no sound when the air is removed from the jar?
These two videos demonstrate the Allasonic effect. The speed of sound is different in a liquid with air bubbles because the density is different. As the bubbles burst, the speed of sound changes, causing the frequency of sound waves in the liquid column to change, thus changing the pitch. Example: one , two . What do you hear in each case?
The Zube Tube is a toy that has a spring inside attached to two plastic cups on either end. Vibrations in the spring travel at different speeds so a sound starting at one end (for example a click when you shake the tube and the spring hits the cup) ends up changing pitch at the other end as the various frequencies arrive. In other words this is a nonlinear system. See if you can figure out from the video which frequencies travel faster, high frequencies or low.

Mini-lab on measuring the speed of sound .

Questions on Wave Speed:

\(f=1/T,\quad v=f\lambda ,\quad v=\omega /k,\quad k=2\pi /\lambda,\quad \omega =2\pi f,\quad y(x,t)=A\cos (kx-\omega t+\phi ),\quad v=\sqrt{B/Q}\)

Light travels at \(3.0\times 10^{8}\text{ m/s}\) but sound waves travel at about \(344\text{ m/s}\). What is the time delay for light and sound to arrive from a source that is \(10,000\text{ m}\) away (this can be used to get an approximate distance to a thunderstorm)?
What two mistakes are made in science fiction movies where you see and hear an explosion in space at the same time?
Consult the table for the speed of sound in various substances. If you have one ear in the water and one ear out while swimming in a lake and a bell is rung that is half way in the water some distance away, which ear hears the sound first?
At \(20\text{C}\) the speed of sound is \(344\text{ m/s}\). How far does sound travel in \(1\text{ s}\)? How far does sound travel in \(60\text{ s}\)?
Compare the last two answers with the distance traveled by light which has a speed of \(3.0\times 10^{8}\text{ m/s}\). Why do you see something happen before you hear it?
The speed of sound in water is \(1482\text{ m/s}\). How far does sound travel under water in \(1\text{ s}\)? How far does sound travel under water in \(60\text{ s}\)?
What happens to the speed of sound in air as temperature increases?
Using the equation for the speed of sound at different temperatures, what is the speed of sound on a hot day when the temperature is \(30^{\circ}\text{C}\)? Hint: \(v = 344\text{ m/s} + 0.6 (T - 20)\) where \(T\) is the temperature in Celsius.
Using the speed of sound at \(30^{\circ}\text{C}\) from the last question, recalculate the distance traveled for the cases in question four.
Suppose on a cold day the temperature is \(-10^{\circ}\text{C}\: (14^{\circ}\text{F}\)). You are playing in the marching band outside. How long does it take the sound from the band to reach the spectators if they are \(100\text{ m}\) away?
What is the difference in the speed of sound in air on a hot day (\(40^{\circ}\text{C}\)) and a cold day (\(0^{\circ}\text{C}\))?
What would an orchestra sound like if different instruments produced sounds that traveled at different speeds?
The speed of a wave is fixed by the medium it travels in so, for a given situation, is usually constant. What happens to the frequency of a wave if the wavelength is doubled?
What happens to the wavelength of a wave if the frequency is doubled and has the same speed?
Suppose a sound wave has a frequency \(200\text{ Hz}\). If the speed of sound is \(343\text{ m/s}\), what wavelength is this wave?
What factors determine the speed of sound in air?
Why do sound waves travel faster through liquids than air?
Why do sound waves travel faster through solids than liquids?
The speed of sound in a fluid is given by \(v=\sqrt{B/Q}\) where \(B\) is the Bulk Modulus (compressibility) and \(Q\) is the density. What happens to the speed if the density of the fluid increases?
What must be true about the compressibility, \(B\), of water versus air, given that sound travels faster in water and water is denser than air?
The speed of sound in a fluid is given by \(v=\sqrt{B/Q}\) where \(B\) is the Bulk Modulus (compressibility) and \(Q\) is the density. Can you think of a clever way to measure the Bulk Modulus of a fluid if you had an easy way to measure the speed of sound in a fluid? Explain.
The speed of sound on a string is given by \(v=\sqrt{T/\mu}\) where \(T\) is the tension in Newtons and \(\mu\) is the linear density (thickness) in \(\text{kg/m}\). You also know that \(v=f\lambda\). Give two ways of changing the frequency of vibration of a guitar string based on the knowledge of these two equations.
For the previous question, increasing the tension does what to the frequency? What does using a denser string do to the frequency?
The following graph is of a wave, frozen in time at \(t = 0\). The equation describing the wave is \(y(x,t)=A\cos (kx-\omega t+\phi )\). Sketch the effect of doubling the amplitude, \(A\).

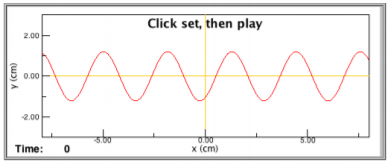
Figure \(\PageIndex{1}\)

For the following graph of a wave, sketch the effect of doubling the wavelength.

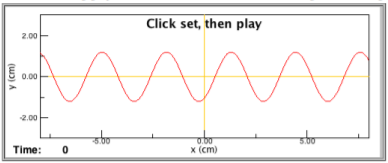
Figure \(\PageIndex{2}\)

The mathematical description of a sine wave is given by \(y(x,t)=A\cos (kx-\omega t+\phi )\). Explain what each of the terms \((A, k, \omega, \phi )\) represent.

15.1 The Electromagnetic Spectrum

Section learning objectives.

By the end of this section, you will be able to do the following:

Define the electromagnetic spectrum, and describe it in terms of frequencies and wavelengths
Describe and explain the differences and similarities of each section of the electromagnetic spectrum and the applications of radiation from those sections

Teacher Support

The learning objectives in this section will help your students master the following standards

(A) examine and describe oscillatory motion and wave propagation in various types of media;
(B) investigate and analyze characteristics of waves, including velocity, frequency, amplitude, and wavelength, and calculate using the relationship between wave speed, frequency, and wavelength;
(C) compare characteristics and behaviors of transverse waves, including electromagnetic waves and the electromagnetic spectrum, and characteristics and behaviors of longitudinal waves, including sound waves; and
(F) describe the role of wave characteristics and behaviors in medical and industrial applications.

In addition, the High School Physics Laboratory Manual addresses content in this section in the lab titled: Light and Color, as well as the following standards:

(C) compare characteristics and behaviors of transverse waves, including electromagnetic waves and the electromagnetic spectrum, and characteristics and behaviors of longitudinal waves, including sound waves.
(B) compare and explain the emission spectra produced by various atoms.

Section Key Terms

[BL] Explain that the term spectrum refers to a physical property that has a broad range with values that are continuous in some cases and, in other cases, discrete. Ask for other examples of spectra, for example, sound, people’s heights, etc.

[OL] Ask students to name ways that sunlight affects Earth. Provide examples that students don’t name: photosynthesis, weather, climate, seasons, warming, etc. Discuss energy transformations that take place after light enters the atmosphere, such as transformations in food chains and ecosystems. Ask students if they can explain how the energy in fossil fuels was originally light energy.

Misconception Alert

The light we can see is called visible light. Dispel any misconceptions that visible light is somehow different from radiation we cannot see, except for frequency and wavelength. The fact that some radiation is visible has to do with how the eye functions, not with the radiation itself.

The Electromagnetic Spectrum

We generally take light for granted, but it is a truly amazing and mysterious form of energy. Think about it: Light travels to Earth across millions of kilometers of empty space. When it reaches us, it interacts with matter in various ways to generate almost all the energy needed to support life, provide heat, and cause weather patterns. Light is a form of electromagnetic radiation (EMR) . The term light usually refers to visible light , but this is not the only form of EMR. As we will see, visible light occupies a narrow band in a broad range of types of electromagnetic radiation.

[OL] Discuss electric, magnetic, and gravitational fields. Point out how these three fields are similar, and how they differ.

[AL] Describe vectors as having magnitude and direction, and explain that fields are vector quantities. In these cases, the fields are made up of forces acting in a direction.

Electromagnetic radiation is generated by a moving electric charge, that is, by an electric current. As you will see when you study electricity, an electric current generates both an electric field , E , and a magnetic field , B . These fields are perpendicular to each other. When the moving charge oscillates, as in an alternating current, an EM wave is propagated. Figure 15.2 shows how an electromagnetic wave moves away from the source—indicated by the ~ symbol.

[BL] Review wave properties: frequency, wavelength, and amplitude. Ask students to recall sound and water waves, and explain how they relate to these properties.

[OL] Explain that an important difference between EM waves and other waves is that they can travel across empty space.

[AL] Ask if students remember the differences between longitudinal and transverse waves. Give examples. Explain that waves carry energy, not matter.

Watch Physics

Electromagnetic waves and the electromagnetic spectrum.

This video, link below, is closely related to the following figure. If you have questions about EM wave properties, the EM spectrum, how waves propagate, or definitions of any of the related terms, the answers can be found in this video .

Grasp Check

In an electromagnetic wave, how are the magnetic field, the electric field, and the direction of propagation oriented to each other?

All three are parallel to each other and are along the x -axis.
All three are mutually perpendicular to each other.
The electric field and magnetic fields are parallel to each other and perpendicular to the direction of propagation.
The magnetic field and direction of propagation are parallel to each other along the y -axis and perpendicular to the electric field.

Direct students to use this video as a way of connecting to the information in the following two figures, as well as to the following table.

Virtual Physics

Radio waves and electromagnetic fields.

This simulation demonstrates wave propagation. The EM wave is propagated from the broadcast tower on the left, just as in Figure 15.2 . You can make the wave yourself or allow the animation to send it. When the wave reaches the antenna on the right, it causes an oscillating current. This is how radio and television signals are transmitted and received.

Where do radio waves fall on the electromagnetic spectrum?

Radio waves have the same wavelengths as visible light.
Radio waves fall on the high-frequency side of visible light.
Radio waves fall on the short-wavelength side of visible light.
Radio waves fall on the low-frequency side of visible light.

Connect the discussion from the previous video, in which the generation of an electromagnetic wave is described, to this application of transmission and reception of electromagnetic waves. In particular, point out how the reception of the radio wave is essentially identical to the method by which the wave is generated. Explain also that these electromagnetic waves are the carrier waves on which audio or visual signals—either analog or digital—are placed, so that they can be transmitted to receivers within a certain range of the broadcast antenna.

From your study of sound waves, recall these features that apply to all types of waves:

Wavelength —The distance between two wave crests or two wave troughs, expressed in various metric measures of distance
Frequency —The number of wave crests that pass a point per second, expressed in hertz (Hz or s –1 )
Amplitude : The height of the crest above the null point

As mentioned, electromagnetic radiation takes several forms. These forms are characterized by a range of frequencies. Because frequency is inversely proportional to wavelength, any form of EMR can also be represented by its range of wavelengths. Figure 15.3 shows the frequency and wavelength ranges of various types of EMR. With how many of these types are you familiar?

Take a few minutes to study the positions of the various types of radiation on the EM spectrum, above. The narrow band that is visible light extends from lower-frequency red light to higher-frequency violet light. Frequencies just below the visible are called infrared (below red) and those just above are ultraviolet (beyond violet). Radio waves , which overlap with the frequencies used for media broadcasts of TV and radio signals, occupy frequencies even lower than infrared (IR). The microwave radiation that you see on the diagram is the same radiation that is used in a microwave oven. What we feel as radiant heat is also a form of low-frequency EMR. The high-frequency radiation to the right of ultraviolet (UV) includes X-rays and gamma (γ) rays.

[BL] Notice that most harmful forms of EM radiation are on the high-frequency end of the spectrum.

[OL] Ask which forms of EM radiation students have heard about. Ask them to describe the types of radiation they remember, and correct any misconceptions. Discuss the difference between ionizing radiation and nonionizing radiation, and the difference between electromagnetic radiation and other types of radiation—alpha, beta, etc.

Heat waves, a type of infrared radiation, are basically no different from other EM waves. We feel them as heat because they have a frequency that interacts with our bodies in a way that transforms EM energy into thermal energy.

Boundless Physics

Maxwell’s Equations

The Scottish physicist James Clerk Maxwell (1831–1879) is regarded widely to have been the greatest theoretical physicist of the nineteenth century. Although he died young, Maxwell not only formulated a complete electromagnetic theory, represented by Maxwell’s equations , he also developed the kinetic theory of gases, and made significant contributions to the understanding of color vision and the nature of Saturn’s rings.

Maxwell brought together all the work that had been done by brilliant physicists, such as Ørsted, Coulomb, Ampere, Gauss, and Faraday, and added his own insights to develop the overarching theory of electromagnetism. Maxwell’s equations are paraphrased here in words because their mathematical content is beyond the level of this text. However, the equations illustrate how apparently simple mathematical statements can elegantly unite and express a multitude of concepts—why mathematics is the language of science.

Electric field lines originate on positive charges and terminate on negative charges. The electric field is defined as the force per unit charge on a test charge, and the strength of the force is related to the electric constant, ε 0 .
Magnetic field lines are continuous, having no beginning or end. No magnetic monopoles are known to exist. The strength of the magnetic force is related to the magnetic constant, μ 0 .
A changing magnetic field induces an electromotive force (emf) and, hence, an electric field. The direction of the emf opposes the change, changing direction of the magnetic field.
Magnetic fields are generated by moving charges or by changing electric fields.

Maxwell’s complete theory shows that electric and magnetic forces are not separate, but different manifestations of the same thing—the electromagnetic force. This classical unification of forces is one motivation for current attempts to unify the four basic forces in nature—the gravitational, electromagnetic, strong nuclear, and weak nuclear forces. The weak nuclear and electromagnetic forces have been unified, and further unification with the strong nuclear force is expected; but, the unification of the gravitational force with the other three has proven to be a real head-scratcher.

One final accomplishment of Maxwell was his development in 1855 of a process that could produce color photographic images. In 1861, he and photographer Thomas Sutton worked together on this process. The color image was achieved by projecting red, blue, and green light through black-and-white photographs of a tartan ribbon, each photo itself exposed in different-colored light. The final image was projected onto a screen (see Figure 15.4 ).

Features that encouraged mathematicians and physicists to accept Maxwell’s equations is that they are seen as being both elegant and—considering the difference between an electric charge and a magnetic dipole, which give rise to the respective fields—essentially symmetrical. When scientists are looking for an approach to developing a new theory, they usually begin with the simplest and most symmetrical explanations. An example of such symmetry is the fact that electrons and protons have equal and opposite charges. You can see the symmetry in the four statements, given above, that describe the equations. The first two statements show a similar treatment of electric and magnetic fields, and the last two describe how a magnetic field can generate an electric field, and vice versa.

From our present-day perspective, we can now see the significance of Maxwell’s equations. This was the first step in the quest to unify all natural forces under one theory. After Maxwell unified the electric and magnetic forces as the electromagnetic force, others unified this force with the weak nuclear force, and there is evidence that the strong nuclear force can be unified with the electroweak force. The only force that has resisted unification with the others is the gravitational force. A theory that would unify all forces is often referred as a grand unified theory or a theory of everything . The quest for such a theory is still underway.

According to Maxwell’s equations, electromagnetic force gives rise to electric force and magnetic force.
According to Maxwell’s equations, electric force and magnetic force are different manifestations of electromagnetic force.
According to Maxwell’s equations, electric force is the cause of electromagnetic force.
According to Maxwell’s equations, magnetic force is the cause of electromagnetic force.

Characteristics of Electromagnetic Radiation

All the EM waves mentioned above are basically the same form of radiation. They can all travel across empty space, and they all travel at the speed of light in a vacuum. The basic difference between types of radiation is their differing frequencies. Each frequency has an associated wavelength. As frequency increases across the spectrum, wavelength decreases. Energy also increases with frequency. Because of this, higher frequencies penetrate matter more readily. Some of the properties and uses of the various EM spectrum bands are listed in Table 15.1 .

[BL] Explain transparency and opacity. Discuss how some materials are transparent to certain frequencies but opaque to others. Ask students for examples of materials that can be penetrated by some EM frequencies but not by others. Ask for examples of materials that are transparent to visible light and materials that are opaque to visible light.

[OL] Ask students why a lead apron is laid across dental patients during dental X-rays. Explain that X-rays are at the high-energy end of the spectrum and that they are very penetrating. They are only stopped by very dense materials, such as lead.

[AL] Ask if students can explain Earth’s greenhouse effect in terms of the penetrating power of various frequencies of EM radiation. Explain that the atmosphere is more transparent to visible light than to heat waves. Visible light penetrates the atmosphere and warms Earth’s surface. The heated surface radiates heat waves, which are trapped partially by certain gases in the atmosphere.

The narrow band of visible light is a combination of the colors of the rainbow. Figure 15.5 shows the section of the EM spectrum that includes visible light. The frequencies corresponding to these wavelengths are 4.0 × 10 14 s −1 4.0 × 10 14 s −1 at the red end to 7.9 × 10 14 s −1 7.9 × 10 14 s −1 at the violet end. This is a very narrow range, considering that the EM spectrum spans about 20 orders of magnitude.

[BL] Review the primary and secondary colors of pigments. Note that this is subtractive color mixing.

[OL] Explain the difference between subtractive and additive color mixing. The colors on the subtractive color wheel are made by pigments that absorb all colors but one. Therefore, when these colors all overlap, all light is absorbed and the result is black. White light is a combination of all colors, so when all colors are added together on the additive color wheel, the result is white. Explain that cyan is a shade of blue and that magenta is a shade of red.

Tips For Success

Wavelengths of visible light are often given in nanometers, nm. One nm equals 10 −9 10 −9 m. For example, yellow light has a wavelength of about 600 nm, or 6 × 10 −7 6 × 10 −7 m.

As a child, you probably learned the color wheel, shown on the left in Figure 15.6 . It helps if you know what color results when you mix different colors of paint together. Mixing two of the primary pigment colors—magenta, yellow, or cyan—together results in a secondary color. For example, mixing cyan and yellow makes green. This is called subtractive color mixing. Mixing different colors of light together is quite different. The diagram on the right shows additive color mixing. In this case, the primary colors are red, green, and blue, and the secondary colors are cyan, magenta, and yellow. Mixing pigments and mixing light are different because materials absorb light by a different set of rules than does the perception of light by the eye. Notice that, when all colors are subtracted, the result is no color, or black. When all colors are added, the result is white light. We see the reverse of this when white sunlight is separated into the visible spectrum by a prism or by raindrops when a rainbow appears in the sky.

Color Vision

This video demonstrates additive color and color filters. Try all the settings except Photons .

A blue filter absorbs blue light, causing the observed light to be a combination of the other colors.
A blue filter absorbs the opposite color of light—orange, causing the observed light to be blue.
A blue filter permits only blue light to pass though, absorbing the other colors and leaving blue light for the observer.
A blue filter permits only the opposite color light—orange—to pass through, leaving orange light for the observer.

Have students adjust the different colored lights for the RGB bulb simulation, first with individual settings, then with combinations of two and three colors to see what colors result and are perceived. Similarly, with the Single Bulb simulation, have students note how different filter settings affect what colors are seen for light with different color components.

Links To Physics

Animal color perception.

The physics of color perception has interesting links to zoology. Other animals have very different views of the world than humans, especially with respect to which colors can be seen. Color is detected by cells in the eye called cones . Humans have three cones that are sensitive to three different ranges of electromagnetic wavelengths. They are called red, blue, and green cones, although these colors do not correspond exactly to the centers of the three ranges. The ranges of wavelengths that each cone detects are red, 500 to 700 nm; green, 450 to 630 nm; and blue, 400 to 500 nm.

Most primates also have three kinds of cones and see the world much as we do. Most mammals other than primates only have two cones and have a less colorful view of things. Dogs, for example see blue and yellow, but are color blind to red and green. You might think that simpler species, such as fish and insects, would have less sophisticated vision, but this is not the case. Many birds, reptiles, amphibians, and insects have four or five different cones in their eyes. These species don’t have a wider range of perceived colors, but they see more hues, or combinations of colors. Also, some animals, such as bees or rattlesnakes, see a range of colors that is as broad as ours, but shifted into the ultraviolet or infrared.

These differences in color perception are generally adaptations that help the animals survive. Colorful tropical birds and fish display some colors that are too subtle for us to see. These colors are believed to play a role in the species mating rituals. Figure 15.7 shows the colors visible and the color range of vision in humans, bees, and dogs.

The symbiotic relationship between plants and their pollinators—bees, birds, etc.—is related to color perception. Plants have evolved to have flowers with colors that bees can see easily, and bees can find those flowers easily to collect the nectar they need for survival.

The belief that bulls are enraged by seeing the color red is a misconception. What did you read in this Links to Physics that shows why this belief is incorrect?

Bulls are color-blind to every color in the spectrum of colors.
Bulls are color-blind to the blue colors in the spectrum of colors.
Bulls are color-blind to the red colors in the spectrum of colors.
Bulls are color-blind to the green colors in the spectrum of colors.

Humans have found uses for every part of the electromagnetic spectrum. We will take a look at the uses of each range of frequencies, beginning with visible light. Most of our uses of visible light are obvious; without it our interaction with our surroundings would be much different. We might forget that nearly all of our food depends on the photosynthesis process in plants, and that the energy for this process comes from the visible part of the spectrum. Without photosynthesis, we would also have almost no oxygen in the atmosphere.

[BL] Ask how different frequencies of EM radiation are applied. Name each frequency range, and ask the students to supply the application, for example, X-rays used in medical imaging.

[OL] Ask students if they know why low-frequency radiation generally has different uses than high-frequency radiation. Explain that it has to do with penetrating power, which is related to health hazards.

[AL] Mention the ranges of TV signals designated very high frequency (VHF) and ultrahigh frequency (UHF). Explain that these frequencies are only relatively high compared to radio broadcast frequencies. Their place in the whole EM spectrum is at the low end.

The low-frequency, infrared region of the spectrum has many applications in media broadcasting. Television, radio, cell phone, and remote-control devices all broadcast and/or receive signals with these wavelengths. AM and FM radio signals are both low-frequency radiation. They are in different regions of the spectrum, but that is not their basic difference. AM and FM are abbreviations for amplitude modulation and frequency modulation . Information in AM signals has the form of changes in amplitude of the radio waves; information in FM signals has the form of changes in wave frequency .

Another application of long-wavelength radiation is found in microwave ovens. These appliances cook or warm food by irradiating it with EM radiation in the microwave frequency range. Most kitchen microwaves use a frequency of 2.45 × 10 9 2.45 × 10 9 Hz. These waves have the right amount of energy to cause polar molecules, such as water, to rotate faster. Polar molecules are those that have a partial charge separation. The rotational energy of these molecules is given up to surrounding matter as heat. The first microwave ovens were called Radaranges because they were based on radar technology developed during World War II.

Radar uses radiation with wavelengths similar to those of microwaves to detect the location and speed of distant objects, such as airplanes, weather formations, and motor vehicles. Radar information is obtained by receiving and analyzing the echoes of microwaves reflected by an object. The speed of the object can be measured using the Doppler shift of the returning waves. This is the same effect you learned about when you studied sound waves. Like sound waves, EM waves are shifted to higher frequencies by an object moving toward an observer, and to lower frequencies by an object moving away from the observer. Astronomers use this same Doppler effect to measure the speed at which distant galaxies are moving away from us. In this case, the shift in frequency is called the red shift , because visible frequencies are shifted toward the lower-frequency, red end of the spectrum.

Exposure to any radiation with frequencies greater than those of visible light carries some health hazards. All types of radiation in this range are known to cause cell damage. The danger is related to the high energy and penetrating ability of these EM waves. The likelihood of being harmed by any of this radiation depends largely on the amount of exposure. Most people try to reduce exposure to UV radiation from sunlight by using sunscreen and protective clothing. Physicians still use X-rays to diagnose medical problems, but the intensity of the radiation used is extremely low. Figure 15.8 shows an X-ray image of a patient’s chest cavity.

One medical-imaging technique that involves no danger of exposure is magnetic resonance imaging (MRI). MRI is an important imaging and research tool in medicine, producing highly detailed two- and three-dimensional images. Radio waves are broadcast, absorbed, and reemitted in a resonance process that is sensitive to the density of nuclei, usually hydrogen nuclei—protons.

Check Your Understanding

Use these questions to assess student achievement of the section’s Learning Objectives. If students are struggling with a specific objective, these questions will help identify any gaps and direct students to the relevant content.

Identify the fields produced by a moving charged particle.

Both an electric field and a magnetic field will be produced.
Neither a magnetic field nor an electric field will be produced.
A magnetic field, but no electric field will be produced.
Only the electric field, but no magnetic field will be produced.
Visible light has higher frequencies and shorter wavelengths than X-rays.
Visible light has lower frequencies and shorter wavelengths than X-rays.
Visible light has higher frequencies and longer wavelengths than X-rays.
Visible light has lower frequencies and longer wavelengths than X-rays.
The wavelength increases.
The wavelength first increases and then decreases.
The wavelength first decreases and then increases.
The wavelength decreases.
X-rays have higher penetrating energy than radio waves.
X-rays have lower penetrating energy than radio waves.
X-rays have a lower frequency range than radio waves.
X-rays have longer wavelengths than radio waves.
both an electric field and a magnetic field
neither a magnetic field nor an electric field
only a magnetic field, but no electric field
only an electric field, but no magnetic field

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

Authors: Paul Peter Urone, Roger Hinrichs
Publisher/website: OpenStax
Book title: Physics
Publication date: Mar 26, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/physics/pages/1-introduction
Section URL: https://openstax.org/books/physics/pages/15-1-the-electromagnetic-spectrum

© Jan 19, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Random article
Teaching guide
Privacy & cookies

radio waves travel faster than sound waves give reason

by Chris Woodford . Last updated: July 23, 2023.

Photo: Sound is energy we hear made by things that vibrate. Photo by William R. Goodwin courtesy of US Navy and Wikimedia Commons .

What is sound?

Photo: Sensing with sound: Light doesn't travel well through ocean water: over half the light falling on the sea surface is absorbed within the first meter of water; 100m down and only 1 percent of the surface light remains. That's largely why mighty creatures of the deep rely on sound for communication and navigation. Whales, famously, "talk" to one another across entire ocean basins, while dolphins use sound, like bats, for echolocation. Photo by Bill Thompson courtesy of US Fish and Wildlife Service .

Robert Boyle's classic experiment

Artwork: Robert Boyle's famous experiment with an alarm clock.

How sound travels

Artwork: Sound waves and ocean waves compared. Top: Sound waves are longitudinal waves: the air moves back and forth along the same line as the wave travels, making alternate patterns of compressions and rarefactions. Bottom: Ocean waves are transverse waves: the water moves back and forth at right angles to the line in which the wave travels.

The science of sound waves

Picture: Reflected sound is extremely useful for "seeing" underwater where light doesn't really travel—that's the basic idea behind sonar. Here's a side-scan sonar (reflected sound) image of a World War II boat wrecked on the seabed. Photo courtesy of U.S. National Oceanographic and Atmospheric Administration, US Navy, and Wikimedia Commons .

Whispering galleries and amphitheaters

Photos by Carol M. Highsmith: 1) The Capitol in Washington, DC has a whispering gallery inside its dome. Photo credit: The George F. Landegger Collection of District of Columbia Photographs in Carol M. Highsmith's America, Library of Congress , Prints and Photographs Division. 2) It's easy to hear people talking in the curved memorial amphitheater building at Arlington National Cemetery, Arlington, Virginia. Photo credit: Photographs in the Carol M. Highsmith Archive, Library of Congress , Prints and Photographs Division.

Measuring waves

Understanding amplitude and frequency, why instruments sound different, the speed of sound.

Photo: Breaking through the sound barrier creates a sonic boom. The mist you can see, which is called a condensation cloud, isn't necessarily caused by an aircraft flying supersonic: it can occur at lower speeds too. It happens because moist air condenses due to the shock waves created by the plane. You might expect the plane to compress the air as it slices through. But the shock waves it generates alternately expand and contract the air, producing both compressions and rarefactions. The rarefactions cause very low pressure and it's these that make moisture in the air condense, producing the cloud you see here. Photo by John Gay courtesy of US Navy and Wikimedia Commons .

Why does sound go faster in some things than in others?

Chart: Generally, sound travels faster in solids (right) than in liquids (middle) or gases (left)... but there are exceptions!

How to measure the speed of sound

Sound in practice, if you liked this article..., find out more, on this website.

Electric guitars
Speech synthesis
Synthesizers

On other sites

Explore Sound : A comprehensive educational site from the Acoustical Society of America, with activities for students of all ages.
Sound Waves : A great collection of interactive science lessons from the University of Salford, which explains what sound waves are and the different ways in which they behave.

Educational books for younger readers

Sound (Science in a Flash) by Georgia Amson-Bradshaw. Franklin Watts/Hachette, 2020. Simple facts, experiments, and quizzes fill this book; the visually exciting design will appeal to reluctant readers. Also for ages 7–9.
Sound by Angela Royston. Raintree, 2017. A basic introduction to sound and musical sounds, including simple activities. Ages 7–9.
Experimenting with Sound Science Projects by Robert Gardner. Enslow Publishers, 2013. A comprehensive 120-page introduction, running through the science of sound in some detail, with plenty of hands-on projects and activities (including welcome coverage of how to run controlled experiments using the scientific method). Ages 9–12.
Cool Science: Experiments with Sound and Hearing by Chris Woodford. Gareth Stevens Inc, 2010. One of my own books, this is a short introduction to sound through practical activities, for ages 9–12.
Adventures in Sound with Max Axiom, Super Scientist by Emily Sohn. Capstone, 2007. The original, graphic novel (comic book) format should appeal to reluctant readers. Ages 8–10.

Popular science

The Sound Book: The Science of the Sonic Wonders of the World by Trevor Cox. W. W. Norton, 2014. An entertaining tour through everyday sound science.

Academic books

Master Handbook of Acoustics by F. Alton Everest and Ken Pohlmann. McGraw-Hill Education, 2015. A comprehensive reference for undergraduates and sound-design professionals.
The Science of Sound by Thomas D. Rossing, Paul A. Wheeler, and F. Richard Moore. Pearson, 2013. One of the most popular general undergraduate texts.

Rate this page

Tell your friends, cite this page, more to explore on our website....

Get the book
Send feedback

Destination

How Radio Waves Travel Faster

How Fast Radio Waves Travel, radio waves play a crucial function in the vast majority of technology solutions you see around you. It is unfortunate that very few are aware of their significance; and many don’t even understand what radio waves mean. So, there are many misconceptions regarding radio waves and their speed.

Radio waves play a major role in many of the technological solutions that we see around us. For the majority of people, they do not even understand the meaning that radio waves have.

There’s a lot of confusion about radio waves. From what they represent to how they work there are only a handful of people have any knowledge about this type of wave. When you’re finished reading this article you will be able to tell anyone else the radio waves and how they work.

What are Radio Waves?

Contrary to what many people think radio waves aren’t the sound you hear from the radio speakers. These are sound waves and not radio waves. Radiation from radio waves is electromagnetic. Radio waves are very like light waves. The only distinction is that you are unable to detect these as light. Consider them to be generated by charged particles that go through acceleration, similar to electrical currents that are changing in time.

Transmitters create them artificially. Radio receivers are required to receive and intercept radio waves by means by an antenna. Radio waves are a method of communication that can be found in numerous technologies. They are utilized in fixed and mobile radio communications, radar and navigation systems streaming, the radio wireless networks satellites for communication and many more.

Radio waves were first discovered in the 1870s by James Clerk Maxwell, the physicist the best well-known for his famous Maxwell’s Equation around the 1870s. A German scientist known in the form of Heinrich Hertz was the one who formulated Maxwell’s theory that radio waves would be a phenomenon.

What is the Speed of Radio Waves in Space?

Space radio waves are traveling at the rate of light (c 299,79×106 milliseconds). This means the distance that radio waves can travel within one minute in space would be 299,792,458 m (983,571,056 feet). Therefore, that radio wave speed is more powerful than sound waves.

Radio waves travel through a variety of different media with different speed. While passing through a medium the speed of radio waves decreases depending on its permittivity, as well as its the permeability.

Radio waves span a distance of 0.04 inch up to more than sixty-two miles. When these waves travel further away from the antenna that broadcasts them, their power decreases.

Main Types of Radio Waves

Low to Medium Frequencies The frequencies listed here are the very first in the spectrum of radio frequencies; the frequency spectrum covers low to medium-sized radio waves. ELF is an acronym in for Extremely Low Frequency, while VLF refers to extremely low frequency. They use frequencies that range from three to thirty kHz. These frequencies are considered to be the most low-frequency radio frequencies. Additionally, their range of operation makes them ideal for communication equipment used in submarines.
Higher Frequencies These frequencies include The frequencies are HF, VHF, and UHF. They are used extensively in broadcast audio and public service radios and cell phones, FM, as well as GPS. The general rule is that low frequencies are more powerful and spread more efficiently than higher frequencies.
Shortwave Radio Shortwave radio uses frequencies that vary between 1.7 Mhz and up to the 30th MHz. They are utilized to transmit broadcast signals of shortwave radio stations across all over the world. For instance, stations such as VOA, BBC and Voice of Russia. VOA, BBC, and Voice of Russia use this frequency band for broadcasting purposes.
Highest Frequencies They comprise SHF (Super High Frequency) in addition to EHF (extremely very high frequency). SHF is commonly utilized in wireless USB as well as Wi-Fi as well as Bluetooth and is employed for radar use. Particularly, super high frequencies only work in straight lines, which means that they bounce off of any obstruction.

What are the Properties of Radio Waves

Radio waves possess distinctive properties which you must understand. These properties will be described below.
They are a type of electromagnetic waves. They possess an extended wavelength than that for infrared radiation.
When they pass through the vacuum and then through a medium, they move with the velocity of light. However, their speed slows when they traverse the medium, according to its permeability.
Radio waves can form by altering electrical currents. Naturally, they could be released by lightning or objects of the night that exhibit magnetic field fluctuations.

How Fast Do Radio Waves Travel? Through Space, Air or Vacuum

The speed at which radio waves travel .

In the past, we have been successful in establishing the fact that electromagnetic waves exist. They are therefore likely behave just like electromagnetic waves, too. One thing common with the electromagnetic wave is that all move at the speed of light in the vacuum. They move at an approximate rate of around 186,000 miles per minute in an atmosphere.

Like audio waves, they are unable to traverse an air vacuum. They are only able to transported through the medium. That is in other words, without a medium there is no way to hear. Radio waves don’t necessarily require any media for their propagation.

Radio waves move in the exact same way as light waves because they’re similar to light waves, but they are not visible. The Radio waves can traverse different media at various speeds. The speed at which they will be able to traverse a certain medium will depend on a few variables.

What is the Function of Radio Waves?

The best method to determine what radio waves do is to employ antennas to explain the idea. For the effectiveness of radio wave it’s require two antennas. One antenna will be the transmitter, and the second will serve as the receiver. Let’s take the radio station as an illustration. In the radio station, voices can be recorded by an audio microphone, and then the system converts it into electrical energy.

The electricity is then transmitted to an analogue (transmitter) at a high altitude. The transmitter increases the strength of the electricity, allowing it to travel as far as is possible. The tiny particles of electric current constantly move between the antenna.

Radio waves then are able to travel with the speed light, or near that speed while the voices remain in them. So, when someone turns on their radio the electrons inside the antenna go between them (vibrated) due to coming radio waves. The resonating effect creates electricity. The electronics component converts the electric signal into audio, which allows you to listen to the recorded voice at the station.

Factors Affecting Wave Speed

The speed of any wave depends upon the properties of the medium through which the wave is traveling. Typically there are two essential types of properties that affect wave speed - inertial properties and elastic properties. Elastic properties are those properties related to the tendency of a material to maintain its shape and not deform whenever a force or stress is applied to it. A material such as steel will experience a very small deformation of shape (and dimension) when a stress is applied to it. Steel is a rigid material with a high elasticity. On the other hand, a material such as a rubber band is highly flexible; when a force is applied to stretch the rubber band, it deforms or changes its shape readily. A small stress on the rubber band causes a large deformation. Steel is considered to be a stiff or rigid material, whereas a rubber band is considered a flexible material. At the particle level, a stiff or rigid material is characterized by atoms and/or molecules with strong attractions for each other. When a force is applied in an attempt to stretch or deform the material, its strong particle interactions prevent this deformation and help the material maintain its shape. Rigid materials such as steel are considered to have a high elasticity. (Elastic modulus is the technical term). The phase of matter has a tremendous impact upon the elastic properties of the medium. In general, solids have the strongest interactions between particles, followed by liquids and then gases. For this reason, longitudinal sound waves travel faster in solids than they do in liquids than they do in gases. Even though the inertial factor may favor gases, the elastic factor has a greater influence on the speed ( v ) of a wave, thus yielding this general pattern:

Inertial properties are those properties related to the material's tendency to be sluggish to changes in its state of motion. The density of a medium is an example of an inertial property . The greater the inertia (i.e., mass density) of individual particles of the medium, the less responsive they will be to the interactions between neighboring particles and the slower that the wave will be. As stated above, sound waves travel faster in solids than they do in liquids than they do in gases. However, within a single phase of matter, the inertial property of density tends to be the property that has a greatest impact upon the speed of sound. A sound wave will travel faster in a less dense material than a more dense material. Thus, a sound wave will travel nearly three times faster in Helium than it will in air. This is mostly due to the lower mass of Helium particles as compared to air particles.

The Speed of Sound in Air

The speed of a sound wave in air depends upon the properties of the air, mostly the temperature, and to a lesser degree, the humidity. Humidity is the result of water vapor being present in air. Like any liquid, water has a tendency to evaporate. As it does, particles of gaseous water become mixed in the air. This additional matter will affect the mass density of the air (an inertial property). The temperature will affect the strength of the particle interactions (an elastic property). At normal atmospheric pressure, the temperature dependence of the speed of a sound wave through dry air is approximated by the following equation:

where T is the temperature of the air in degrees Celsius. Using this equation to determine the speed of a sound wave in air at a temperature of 20 degrees Celsius yields the following solution.

v = 331 m/s + (0.6 m/s/C)•(20 C)

v = 331 m/s + 12 m/s

v = 343 m/s

(The above equation relating the speed of a sound wave in air to the temperature provides reasonably accurate speed values for temperatures between 0 and 100 Celsius. The equation itself does not have any theoretical basis; it is simply the result of inspecting temperature-speed data for this temperature range. Other equations do exist that are based upon theoretical reasoning and provide accurate data for all temperatures. Nonetheless, the equation above will be sufficient for our use as introductory Physics students.)

Look It Up!

Using wave speed to determine distances.

At normal atmospheric pressure and a temperature of 20 degrees Celsius, a sound wave will travel at approximately 343 m/s; this is approximately equal to 750 miles/hour. While this speed may seem fast by human standards (the fastest humans can sprint at approximately 11 m/s and highway speeds are approximately 30 m/s), the speed of a sound wave is slow in comparison to the speed of a light wave. Light travels through air at a speed of approximately 300 000 000 m/s; this is nearly 900 000 times the speed of sound. For this reason, humans can observe a detectable time delay between the thunder and the lightning during a storm. The arrival of the light wave from the location of the lightning strike occurs in so little time that it is essentially negligible. Yet the arrival of the sound wave from the location of the lightning strike occurs much later. The time delay between the arrival of the light wave (lightning) and the arrival of the sound wave (thunder) allows a person to approximate his/her distance from the storm location. For instance if the thunder is heard 3 seconds after the lightning is seen, then sound (whose speed is approximated as 345 m/s) has traveled a distance of

If this value is converted to miles (divide by 1600 m/1 mi), then the storm is a distance of 0.65 miles away.

Another phenomenon related to the perception of time delays between two events is an echo . A person can often perceive a time delay between the production of a sound and the arrival of a reflection of that sound off a distant barrier. If you have ever made a holler within a canyon, perhaps you have heard an echo of your holler off a distant canyon wall. The time delay between the holler and the echo corresponds to the time for the holler to travel the round-trip distance to the canyon wall and back. A measurement of this time would allow a person to estimate the one-way distance to the canyon wall. For instance if an echo is heard 1.40 seconds after making the holler , then the distance to the canyon wall can be found as follows:

The canyon wall is 242 meters away. You might have noticed that the time of 0.70 seconds is used in the equation. Since the time delay corresponds to the time for the holler to travel the round-trip distance to the canyon wall and back, the one-way distance to the canyon wall corresponds to one-half the time delay.

While an echo is of relatively minimal importance to humans, echolocation is an essential trick of the trade for bats. Being a nocturnal creature, bats must use sound waves to navigate and hunt. They produce short bursts of ultrasonic sound waves that reflect off objects in their surroundings and return. Their detection of the time delay between the sending and receiving of the pulses allows a bat to approximate the distance to surrounding objects. Some bats, known as Doppler bats, are capable of detecting the speed and direction of any moving objects by monitoring the changes in frequency of the reflected pulses. These bats are utilizing the physics of the Doppler effect discussed in an earlier unit (and also to be discussed later in Lesson 3 ). This method of echolocation enables a bat to navigate and to hunt.

The Wave Equation Revisited

Like any wave, a sound wave has a speed that is mathematically related to the frequency and the wavelength of the wave. As discussed in a previous unit , the mathematical relationship between speed, frequency and wavelength is given by the following equation.

Using the symbols v , λ , and f , the equation can be rewritten as

Check Your Understanding

1. An automatic focus camera is able to focus on objects by use of an ultrasonic sound wave. The camera sends out sound waves that reflect off distant objects and return to the camera. A sensor detects the time it takes for the waves to return and then determines the distance an object is from the camera. If a sound wave (speed = 340 m/s) returns to the camera 0.150 seconds after leaving the camera, how far away is the object?

Answer = 25.5 m

The speed of the sound wave is 340 m/s. The distance can be found using d = v • t resulting in an answer of 25.5 m. Use 0.075 seconds for the time since 0.150 seconds refers to the round-trip distance.

2. On a hot summer day, a pesky little mosquito produced its warning sound near your ear. The sound is produced by the beating of its wings at a rate of about 600 wing beats per second.

a. What is the frequency in Hertz of the sound wave? b. Assuming the sound wave moves with a velocity of 350 m/s, what is the wavelength of the wave?

Part a Answer: 600 Hz (given)

Part b Answer: 0.583 meters

3. Doubling the frequency of a wave source doubles the speed of the waves.

a. True b. False

Doubling the frequency will halve the wavelength; speed is unaffected by the alteration in the frequency. The speed of a wave depends upon the properties of the medium.

4. Playing middle C on the piano keyboard produces a sound with a frequency of 256 Hz. Assuming the speed of sound in air is 345 m/s, determine the wavelength of the sound corresponding to the note of middle C.

Answer: 1.35 meters (rounded)

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 256 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

5. Most people can detect frequencies as high as 20 000 Hz. Assuming the speed of sound in air is 345 m/s, determine the wavelength of the sound corresponding to this upper range of audible hearing.

Answer: 0.0173 meters (rounded)

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 20 000 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

6. An elephant produces a 10 Hz sound wave. Assuming the speed of sound in air is 345 m/s, determine the wavelength of this infrasonic sound wave.

Answer: 34.5 meters

Let λ = wavelength. Use v = f • λ where v = 345 m/s and f = 10 Hz. Rearrange the equation to the form of λ = v / f. Substitute and solve.

7. Determine the speed of sound on a cold winter day (T=3 degrees C).

Answer: 332.8 m/s

The speed of sound in air is dependent upon the temperature of air. The dependence is expressed by the equation:

v = 331 m/s + (0.6 m/s/C) • T

where T is the temperature in Celsius. Substitute and solve.

v = 331 m/s + (0.6 m/s/C) • 3 C v = 331 m/s + 1.8 m/s v = 332.8 m/s

8. Miles Tugo is camping in Glacier National Park. In the midst of a glacier canyon, he makes a loud holler. He hears an echo 1.22 seconds later. The air temperature is 20 degrees C. How far away are the canyon walls?

Answer = 209 m

The speed of the sound wave at this temperature is 343 m/s (using the equation described in the Tutorial). The distance can be found using d = v • t resulting in an answer of 343 m. Use 0.61 second for the time since 1.22 seconds refers to the round-trip distance.

9. Two sound waves are traveling through a container of unknown gas. Wave A has a wavelength of 1.2 m. Wave B has a wavelength of 3.6 m. The velocity of wave B must be __________ the velocity of wave A.

a. one-ninth b. one-third c. the same as d. three times larger than

The speed of a wave does not depend upon its wavelength, but rather upon the properties of the medium. The medium has not changed, so neither has the speed.

10. Two sound waves are traveling through a container of unknown gas. Wave A has a wavelength of 1.2 m. Wave B has a wavelength of 3.6 m. The frequency of wave B must be __________ the frequency of wave A.

Since Wave B has three times the wavelength of Wave A, it must have one-third the frequency. Frequency and wavelength are inversely related.

Interference and Beats

How Sound, Light, and Radio Waves Travel

What exactly does the term “wave” imply? A wave is a disturbance that moves or spreads from its source. Waves transfer energy, but they do not necessarily carry any mass along with them.

Waves are a form of longitudinal motion. Sound and water waves are mechanical waves, which means they need a medium to travel through. A solid, liquid, or gas may be the medium, and the speed of the wave is determined by the physical characteristics of the medium in which it is traveling.

However, light and radio are not mechanical waves; they can propagate through a vacuum, such as the voids in outer space.

Why Can’t Sound Travel in Space?

Sound waves are caused by air vibrations. We humans hear them when the frequencies range from 20 to 20,000 Hz.

Sound waves are produced when particles in a medium vibrate. These vibrations are transmitted to the following molecules in the medium, thus sound waves cannot travel through space without a medium. The reason we can’t hear anything in outer space is because there isn’t any such thing as a sufficient medium.

We may debate about gases serving as media in space, but gases are unevenly distributed throughout the space. Furthermore, gases are generally less dense in space, so there is too much of a gap between the particles for vibrations to travel effectively.

In basic terms, sound cannot travel in space.

Why Do Sound Waves Require a Medium to Travel?

The water wave is a familiar phenomenon that you can readily picture. The disturbance in water waves occurs at the surface of the water, as evidenced by a rock thrown into a pond or a swimmer splashing the water’s surface repeatedly.

The disturbance in sound waves is caused by a variation in air pressure, as demonstrated by the following: When a speaker’s oscillating cone creates an uproar. There are several types of disturbances associated with earthquakes, some of which are the surface disturbance and pressure changes beneath the surface.

Water waves are one of the most well-known types of waves, and for good reason. Water waves are often and readily observable, so thinking about water waves might help you understand other sorts of waves that aren’t as apparent.

Do Radio Waves Require a Medium to Travel?

No, radio waves are electromagnetic radiation. Electromagnetic waves differ from mechanical waves in that they do not need a medium to travel. This implies that electromagnetic radiation may propagate through both air and solid materials as well as vacuum space.

The wave is the oscillation of some variable within a body in many types of waves, such as sound waves or water waves. The pressure of the air is responsible for sound waves, while the height of the water in a lake or ocean causes water waves.

However, the electric and magnetic fields in space are oscillating which are electromagnetic waves . The electric and magnetic fields are force fields that exist without a medium. They’re simply there. Electric charges and currents give rise to them, and they span the vacuum from their origins through the cosmos.

When an electric charge or current fluctuates, the accompanying magnetic and electric fields likewise fluctuate. However, these waves don’t appear instantly everywhere; instead, they spread at the speed of light from the original source.

Why Doesn’t Light Need a Medium to Travel?

A light wave is an electromagnetic wave. It does not require any medium because it travels through space without relying on medium particles. Light, in a nutshell, is an electromagnetic radiation caused by the disruption of electric and magnetic fields.

The direction of propagation of the electric and magnetic fields which are mutually perpendicular supports each other to travel in a perpendicular direction. Light is capable of traveling without medium because it may be generated and propagated through vacuum (or no medium).

The concept of light’s particles, originally developed by German philosopher and physicist Ernst Mach in the 19th century, implies that light is made up of tiny energy bundle packets known as “photons.” Because light follows the principles of wave-particle duality, it exists in two states: particle and wave. From this perspective, these energized photons travel alone without the assistance of a medium.

Also, it’s from these photons that color is visible to us humans.

Think of it another way.

We understand that light does not require a medium to travel since the speed of light is experimentally constant: it does not vary regardless of the source, detector, or direction in which it travels.

Light and sound clash, the latter which is transmitted through the air (or some other material medium). The speed of sound in all directions is the same if you’re stationary with respect to the air. But if you’re moving with respect to the air, the speed of sound will be the same in all directions relative to the air—which means that sound coming up ahead of you will seem faster, and sounds catching up from behind will appear slower.

Light would act in the same way if it were a disturbance in a medium. However, light’s speed will always be constant under all circumstances. It is a the universal constant after all.

Radio Waves in Space
Why does Radar Use Radio Waves?
How Far Can a Laser Travel?
How and Why We See Colors

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Lots of galaxies shown as small points of light against a dark backdrop.

Why isn’t there any sound in space? An astronomer explains why in space no one can hear you scream

University Distinguished Professor of Astronomy, University of Arizona

Disclosure statement

Chris Impey receives funding from the National Science Foundation.

University of Arizona provides funding as a member of The Conversation US.

View all partners

Curious Kids is a series for children of all ages. If you have a question you’d like an expert to answer, send it to [email protected] .

How far can sound travel through space, since it’s so empty? Is there an echo in space? – Jasmine, age 14, Everson, Washington

In space, no one can hear you scream.

You may have heard this saying. It’s the tagline from the famous 1979 science fiction movie “ Alien .” It’s a scary thought, but is it true? The simple answer is yes, no one can hear you scream in space because there is no sound or echo in space.

I’m a professor of astronomy , which means I study space and how it works. Space is silent – for the most part.

How sound works

To understand why there’s no sound in space, first consider how sound works. Sound is a wave of energy that moves through a solid, a liquid or a gas.

Sound is a compression wave . The energy created when your vocal cords vibrate slightly compresses the air in your throat, and the compressed energy travels outward.

A good analogy for sound is a Slinky toy . If you stretch out a Slinky and push hard on one end, a compression wave travels down the Slinky.

When you talk, your vocal cords vibrate. They jostle air molecules in your throat above your vocal cords, which in turn jostle or bump into their neighbors, causing a sound to come out of your mouth.

Sound moves through air the same way it moves through your throat. Air molecules near your mouth bump into their neighbors, which in turn bump into their neighbors, and the sound moves through the air. The sound wave travels quickly , about 760 miles per hour (1,223 kilometers per hour), which is faster than a commercial jet.

Space is a vacuum

So what about in space?

Space is a vacuum, which means it contains almost no matter. The word vacuum comes from the Latin word for empty .

Sound is carried by atoms and molecules. In space, with no atoms or molecules to carry a sound wave, there’s no sound. There’s nothing to get in sound’s way out in space, but there’s nothing to carry it, so it doesn’t travel at all. No sound also means no echo. An echo happens when a sound wave hits a hard, flat surface and bounces back in the direction it came from.

By the way, if you were caught in space outside your spacecraft with no spacesuit, the fact that no one could hear your cry for help is the least of your problems. Any air you still had in your lungs would expand because it was at higher pressure than the vacuum outside. Your lungs would rupture. In a mere 10 to 15 seconds , you’d be unconscious due to a lack of oxygen.

Sound in the solar system

Scientists have wondered how human voices would sound on our nearest neighboring planets, Venus and Mars. This experiment is hypothetical because Mars is usually below freezing , and its atmosphere is thin, unbreathable carbon dioxide . Venus is even worse – its air is hot enough to melt lead, with a thick carbon dioxide atmosphere.

On Mars, your voice would sound tinny and hollow, like the sound of a piccolo . On Venus , the pitch of your voice would be much deeper, like the sound of a booming bass guitar. The reason is the thickness of the atmosphere. On Mars the thin air creates a high-pitched sound, and on Venus the thick air creates a low-pitched sound. The team that worked this out simulated other solar system sounds , like a waterfall on Saturn’s moon Titan.

Deep space sounds

While space is a good enough vacuum that normal sound can’t travel through it, it’s actually not a perfect vacuum, and it does have some particles floating through it.

Beyond the Earth and its atmosphere, there are five particles in a typical cubic centimeter – the volume of a sugar cube – that are mostly hydrogen atoms. By contrast, the air you are breathing is 10 billion billion (10 19) times more dense. The density goes down with distance from the Sun, and in the space between stars there are 0.1 particles per cubic centimeter. In vast voids between galaxies , it is a million times lower still – fantastically empty.

The voids of space are kept very hot by radiation from stars. The very spread-out matter found there is in a physical state called a plasma .

A plasma is a gas in which electrons are separated from protons. In a plasma, the physics of sound waves get complicated . Waves travel much faster in this low-density medium, and their wavelength is much longer.

In 2022, NASA released a spectacular example of sound in space . It used X-ray data to make an audible recording that represents the way a massive black hole stirs up plasma in the Perseus galaxy cluster, 250 million light years from Earth. The black hole itself emits no sound, but the diffuse plasma around it carries very long wavelength sound waves.

The natural sound is far too low a frequency for the human ear to hear, 57 octaves below middle C, which is the middle note on a piano and in the middle of the range of sound people can hear. But after raising the frequency to the audible range, the result is chilling – it’s the sound of a black hole growling in deep space.

Hello, curious kids! Do you have a question you’d like an expert to answer? Ask an adult to send your question to [email protected] . Please tell us your name, age and the city where you live.

And since curiosity has no age limit – adults, let us know what you’re wondering, too. We won’t be able to answer every question, but we will do our best.

Astrophysics
Curious Kids
Curious Kids US
Vocal cords

Events and Communications Coordinator

Assistant Editor - 1 year cadetship

Executive Dean, Faculty of Health

Lecturer/Senior Lecturer, Earth System Science (School of Science)

Sydney Horizon Educators (Identified)

IMAGES

Difference Between Radio Waves and Sound Waves
Understanding The Physics Behind How Fast Radio Waves Travel
How Sound Waves Travel
How Fast Do Radio Waves Travel?
Physics Education: Sound & Radio Wave Calculations Explained (Stuart Method)
Propagation of Radio Waves

VIDEO

Just passing through the moment!
Travel Faster than Sound
Does Sound Travel Faster in Space?
Car Which Travel Faster Than Sound #shorts #ytshorts
Stress Wave Timer
Understanding "Radio Wave": A Dive into Invisible Signals

COMMENTS

Difference Between Radio Waves and Sound Waves
Radio waves and sound waves are not similar. The main difference between radio waves and sound waves is that radio waves are a type of electromagnetic wave. ... Typically, sound can travel faster in liquids and even faster in solids. Sound can travel through diamond at a speed of about 12 km per second 1. Sound is really a pressure wave, ...
Why does a blast wave travel faster than sound?
The underlying reason why the usual sound wave and the blast wave travel at different speeds is that the air (or any real-life acoustic media for that matter) is non-linear. The acoustic waves travel by adiabatic compression and expansion if the medium. This is profoundly non-linear process. from.
Why are waves in the electromagnetic spectrum all the same speed?
The analogous terms for sound waves are ultrasound, acoustic and infrasound. A gamma waves oscillates faster than a radio wave but propagates at the same speed. It is possible for some sound and EM waves to have the same frequency, but their speed (and therefore wavelengths) will be different because they do not propagate in the same medium.
Radio Waves
Radio waves have the longest wavelengths in the electromagnetic spectrum. They range from the length of a football to larger than our planet. Heinrich Hertz proved the existence of radio waves in the late 1880s. He used a spark gap attached to an induction coil and a separate spark gap on a receiving antenna. When waves created by the sparks of ...
5.1.1: Speeds of Different Types of Waves
The speed of a wave is fixed by the type of wave and the physical properties of the medium in which it travels. An exception is electromagnetic waves which can travel through a vacuum. For most substances the material will vibrate obeying a Hooke's law force as a wave passes through it and the speed will not depend on frequency.
15.1 The Electromagnetic Spectrum
Ask students to recall sound and water waves, and explain how they relate to these properties. [OL] Explain that an important difference between EM waves and other waves is that they can travel across empty space. [AL] Ask if students remember the differences between longitudinal and transverse waves. Give examples.
Sound
Measuring waves. All sound waves are the same: they travel through a medium by making atoms or molecules shake back and forth. But all sound waves are different too. There are loud sounds and quiet sounds, high-pitched squeaks and low-pitched rumbles, and even two instruments playing exactly the same musical note will produce sound waves that are quite different.
Understanding Radio Waves: Nature and Properties
Understanding Radio Waves: Nature and Properties. 2024-03-18 by K5HRA. Radio waves, the unsung heroes of the electromagnetic spectrum, serve as the cornerstone of amateur radio, enabling enthusiasts to experiment, communicate, and explore a world invisible to the naked eye. These waves, oscillating electric and magnetic fields that travel ...
Understanding The Physics Behind How Fast Radio Waves Travel
Space radio waves are traveling at the rate of light (c 299,79×106 milliseconds). This means the distance that radio waves can travel within one minute in space would be 299,792,458 m (983,571,056 feet). Therefore, that radio wave speed is more powerful than sound waves. Radio waves travel through a variety of different media with different speed.
Physics Tutorial: The Speed of Sound
The speed of a sound wave refers to how fast a sound wave is passed from particle to particle through a medium. The speed of a sound wave in air depends upon the properties of the air - primarily the temperature. Sound travels faster in solids than it does in liquids; sound travels slowest in gases such as air. The speed of sound can be calculated as the distance-per-time ratio or as the ...
How Sound, Light, and Radio Waves Travel
Waves are a form of longitudinal motion. Sound and water waves are mechanical waves, which means they need a medium to travel through. A solid, liquid, or gas may be the medium, and the speed of the wave is determined by the physical characteristics of the medium in which it is traveling. However, light and radio are not mechanical waves; they ...
Understanding Radio Waves vs. Sound Waves
Radio waves are electromagnetic waves, meaning they don't require a medium to travel. They can easily traverse the vacuum of space. Sound waves, on the other hand, are mechanical and need a medium (like air, water, or solids) to propagate. Since space is a vacuum, sound waves can't travel through it. 3.
Relative speed of sound in solids, liquids, and gases
The stiffer the medium the faster the sound waves will travel through it. This is because in a stiff material, each molecule is more interconnected to the other molecules around it. So any disturbance gets transmitted faster down the line. The other factor that determines the speed of a sound wave is the density of the medium.
Sound is a longitudinal wave (article)
Kent Kellenberger. 7 years ago. Longitudinal sound waves are used in ultrasound to do prenatal screening. Also, you can clean teeth using ultrasound, knock out small cancers, and obliterate kidney stones, all using ultrasound, which is sounds at a frequency in excess of 20,000 Hz.
What travels faster: a radio signal or sound in air?
What propagates faster: a radio signal or sound in air? Where does sound travel faster; water or air? A sound wave in a solid has a frequency of 15.0 kHz and a wavelength of 0.333 m. (a) What would be the wave speed, and how much faster is this speed than the speed of sound in air? A sound wave in a solid has a frequency of 15.0 KHz and a ...
How do radio waves physically "travel"?
21 1 2. Radio waves are electromagnetic in nature. Recall that EM waves do not require medium for propagation. The continuously changing electric field of an EM wave generates continuously changing magnetic field and vice versa. This is a never ending phenomenon. - Mitchell. Jun 2, 2017 at 12:36.
6.1.5 Transmission of Sound Waves
Explain why sound travels further at night than during the day. Step 1: Identify the difference in conditions between the day and the night. Step 2: Consider the effect of sound waves travelling between the two air temperatures. Step 3: Explain the motion of the waves during the day and the night.
Is there any sound in space? An astronomer explains
Sound is carried by atoms and molecules. In space, with no atoms or molecules to carry a sound wave, there's no sound. There's nothing to get in sound's way out in space, but there's ...
Device Makes Radio Waves Travel Faster Than Light
Singleton said the polarization synchrotron basically abuses radio waves so severely that they finally give in and travel faster than light. This may be what happens in pulsars, as well ...
waves
The signal is sent to the brain where it is interpreted. As the sound wave progresses through the air, its energy slowly dissipates. This is why sound is louder closer to the source and quieter further from the source. Wave interference occurs when two or more waves disturb the same air molecules.
Why isn't there any sound in space? An astronomer explains why in space
The sound wave travels quickly, about 760 miles per hour (1,223 kilometers per hour), which is faster than a commercial jet. Sound waves are created when matter vibrates. Space is a vacuum
Why do sound waves travel faster in water than light waves?
The exsit of medium will then reduce the travel of light, the water reduce stronger than air. Sound is produced by the vibration of matter, it travels by the matter interact with each other. So it depend on the medium, the density of water are larger than air, then the interaction between the water molecule are larger than air molecule.
How Does Sound Travel From One Medium To Another?
The reason behind this is very simple: you see, when sound originates from a point, travels through a medium, and then encounters a solid object, it loses some of its energy. In other words, a change in the medium triggers a reduction in the energy being carried by the sound wave. That's essentially why sounds lose their 'loudness' when ...

Difference Between Radio Waves and Sound Waves

What are Radio Waves

What are Sound Waves

Wave classification

About the Author: Nipun

5.1.1: Speeds of Different Types of Waves

Video/audio examples:

Questions on Wave Speed:

15.1 The Electromagnetic Spectrum

Teacher Support

Section Key Terms

Misconception Alert

The Electromagnetic Spectrum

Watch Physics

Grasp Check

Virtual Physics

Boundless Physics

Characteristics of Electromagnetic Radiation

Tips For Success

Color Vision

Links To Physics

Check Your Understanding

What is sound?

Robert Boyle's classic experiment

How sound travels

The science of sound waves

Whispering galleries and amphitheaters

Measuring waves

Why does sound go faster in some things than in others?

How to measure the speed of sound

On other sites

Educational books for younger readers

Popular science

Academic books

Rate this page

How Radio Waves Travel Faster

What are Radio Waves?

What is the Speed of Radio Waves in Space?

Main Types of Radio Waves

What are the Properties of Radio Waves

How Fast Do Radio Waves Travel? Through Space, Air or Vacuum

What is the Function of Radio Waves?

Leave a Reply

Recent Posts

Popular Posts

Factors Affecting Wave Speed

The Speed of Sound in Air

Look It Up!

The Wave Equation Revisited

Check Your Understanding

How Sound, Light, and Radio Waves Travel

Why Can’t Sound Travel in Space?

Why Do Sound Waves Require a Medium to Travel?

Do Radio Waves Require a Medium to Travel?

Why Doesn’t Light Need a Medium to Travel?

Related posts:

Leave a Comment

Why isn’t there any sound in space? An astronomer explains why in space no one can hear you scream

Disclosure statement

How sound works

Space is a vacuum

Sound in the solar system

Deep space sounds

Events and Communications Coordinator

Assistant Editor - 1 year cadetship

Executive Dean, Faculty of Health

Lecturer/Senior Lecturer, Earth System Science (School of Science)

Sydney Horizon Educators (Identified)

IMAGES

VIDEO

COMMENTS