tour vs circuit

Discrete Mathematics An Open Introduction

Oscar Levin

Section 4.4 Euler Paths and Circuits

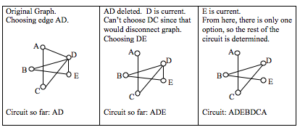
Investigate 35.

An Euler path , in a graph or multigraph, is a walk through the graph which uses every edge exactly once. An Euler circuit is an Euler path which starts and stops at the same vertex. Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or circuit.

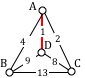
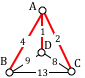
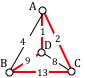
Which of the graphs below have Euler paths? Which have Euler circuits?

List the degrees of each vertex of the graphs above. Is there a connection between degrees and the existence of Euler paths and circuits?

Is it possible for a graph with a degree 1 vertex to have an Euler circuit? If so, draw one. If not, explain why not. What about an Euler path?

What if every vertex of the graph has degree 2. Is there an Euler path? An Euler circuit? Draw some graphs.

Below is part of a graph. Even though you can only see some of the vertices, can you deduce whether the graph will have an Euler path or circuit?

If we start at a vertex and trace along edges to get to other vertices, we create a walk through the graph. More precisely, a walk in a graph is a sequence of vertices such that every vertex in the sequence is adjacent to the vertices before and after it in the sequence. If the walk travels along every edge exactly once, then the walk is called an Euler path (or Euler walk ). If, in addition, the starting and ending vertices are the same (so you trace along every edge exactly once and end up where you started), then the walk is called an Euler circuit (or Euler tour ). Of course if a graph is not connected, there is no hope of finding such a path or circuit. For the rest of this section, assume all the graphs discussed are connected.

The bridges of Königsberg problem is really a question about the existence of Euler paths. There will be a route that crosses every bridge exactly once if and only if the graph below has an Euler path:

This graph is small enough that we could actually check every possible walk that does not reuse edges, and in doing so convince ourselves that there is no Euler path (let alone an Euler circuit). On small graphs which do have an Euler path, it is usually not difficult to find one. Our goal is to find a quick way to check whether a graph has an Euler path or circuit, even if the graph is quite large.

One way to guarantee that a graph does not have an Euler circuit is to include a “spike,” a vertex of degree 1.

The vertex \(a\) has degree 1, and if you try to make an Euler circuit, you see that you will get stuck at the vertex. It is a dead end. That is, unless you start there. But then there is no way to return, so there is no hope of finding an Euler circuit. There is however an Euler path. It starts at the vertex \(a\text{,}\) then loops around the triangle. You will end at the vertex of degree 3.

You run into a similar problem whenever you have a vertex of any odd degree. If you start at such a vertex, you will not be able to end there (after traversing every edge exactly once). After using one edge to leave the starting vertex, you will be left with an even number of edges emanating from the vertex. Half of these could be used for returning to the vertex, the other half for leaving. So you return, then leave. Return, then leave. The only way to use up all the edges is to use the last one by leaving the vertex. On the other hand, if you have a vertex with odd degree that you do not start a path at, then you will eventually get stuck at that vertex. The path will use pairs of edges incident to the vertex to arrive and leave again. Eventually all but one of these edges will be used up, leaving only an edge to arrive by, and none to leave again.

What all this says is that if a graph has an Euler path and two vertices with odd degree, then the Euler path must start at one of the odd degree vertices and end at the other. In such a situation, every other vertex must have an even degree since we need an equal number of edges to get to those vertices as to leave them. How could we have an Euler circuit? The graph could not have any odd degree vertex as an Euler path would have to start there or end there, but not both. Thus for a graph to have an Euler circuit, all vertices must have even degree.

The converse is also true: if all the vertices of a graph have even degree, then the graph has an Euler circuit, and if there are exactly two vertices with odd degree, the graph has an Euler path. To prove this is a little tricky, but the basic idea is that you will never get stuck because there is an “outbound” edge for every “inbound” edge at every vertex. If you try to make an Euler path and miss some edges, you will always be able to “splice in” a circuit using the edges you previously missed.

Euler Paths and Circuits

A graph has an Euler circuit if and only if the degree of every vertex is even.

A graph has an Euler path if and only if there are at most two vertices with odd degree.

Since the bridges of Königsberg graph has all four vertices with odd degree, there is no Euler path through the graph. Thus there is no way for the townspeople to cross every bridge exactly once.

Subsection Hamilton Paths

Suppose you wanted to tour Königsberg in such a way where you visit each land mass (the two islands and both banks) exactly once. This can be done. In graph theory terms, we are asking whether there is a path which visits every vertex exactly once. Such a path is called a Hamilton path (or Hamiltonian path ). We could also consider Hamilton cycles , which are Hamliton paths which start and stop at the same vertex.

Example 4.4.1

Determine whether the graphs below have a Hamilton path.

The graph on the left has a Hamilton path (many different ones, actually), as shown here:

The graph on the right does not have a Hamilton path. You would need to visit each of the “outside” vertices, but as soon as you visit one, you get stuck. Note that this graph does not have an Euler path, although there are graphs with Euler paths but no Hamilton paths.

It appears that finding Hamilton paths would be easier because graphs often have more edges than vertices, so there are fewer requirements to be met. However, nobody knows whether this is true. There is no known simple test for whether a graph has a Hamilton path. For small graphs this is not a problem, but as the size of the graph grows, it gets harder and harder to check wither there is a Hamilton path. In fact, this is an example of a question which as far as we know is too difficult for computers to solve; it is an example of a problem which is NP-complete.

Subsection Exercises

You and your friends want to tour the southwest by car. You will visit the nine states below, with the following rather odd rule: you must cross each border between neighboring states exactly once (so, for example, you must cross the Colorado-Utah border exactly once). Can you do it? If so, does it matter where you start your road trip? What fact about graph theory solves this problem?

This is a question about finding Euler paths. Draw a graph with a vertex in each state, and connect vertices if their states share a border. Exactly two vertices will have odd degree: the vertices for Nevada and Utah. Thus you must start your road trip at in one of those states and end it in the other.

Which of the following graphs contain an Euler path? Which contain an Euler circuit?

• \(K_5\text{.}\)
• \(K_{5,7}\)
• \(K_{2,7}\)
• \(K_4\) does not have an Euler path or circuit.
• \(K_5\) has an Euler circuit (so also an Euler path).
• \(K_{5,7}\) does not have an Euler path or circuit.
• \(K_{2,7}\) has an Euler path but not an Euler circuit.
• \(C_7\) has an Euler circuit (it is a circuit graph!)
• \(P_7\) has an Euler path but no Euler circuit.

Edward A. Mouse has just finished his brand new house. The floor plan is shown below:

Edward wants to give a tour of his new pad to a lady-mouse-friend. Is it possible for them to walk through every doorway exactly once? If so, in which rooms must they begin and end the tour? Explain.

Is it possible to tour the house visiting each room exactly once (not necessarily using every doorway)? Explain.

After a few mouse-years, Edward decides to remodel. He would like to add some new doors between the rooms he has. Of course, he cannot add any doors to the exterior of the house. Is it possible for each room to have an odd number of doors? Explain.

For which \(n\) does the graph \(K_n\) contain an Euler circuit? Explain.

When \(n\) is odd, \(K_n\) contains an Euler circuit. This is because every vertex has degree \(n-1\text{,}\) so an odd \(n\) results in all degrees being even.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain an Euler path? An Euler circuit? Explain.

If both \(m\) and \(n\) are even, then \(K_{m,n}\) has an Euler circuit. When both are odd, there is no Euler path or circuit. If one is 2 and the other is odd, then there is an Euler path but not an Euler circuit.

For which \(n\) does \(K_n\) contain a Hamilton path? A Hamilton cycle? Explain.

All values of \(n\text{.}\) In particular, \(K_n\) contains \(C_n\) as a subgroup, which is a cycle that includes every vertex.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain a Hamilton path? A Hamilton cycle? Explain.

As long as \(|m-n| \le 1\text{,}\) the graph \(K_{m,n}\) will have a Hamilton path. To have a Hamilton cycle, we must have \(m=n\text{.}\)

A bridge builder has come to Königsberg and would like to add bridges so that it is possible to travel over every bridge exactly once. How many bridges must be built?

If we build one bridge, we can have an Euler path. Two bridges must be built for an Euler circuit.

Below is a graph representing friendships between a group of students (each vertex is a student and each edge is a friendship). Is it possible for the students to sit around a round table in such a way that every student sits between two friends? What does this question have to do with paths?

We are looking for a Hamiltonian cycle, and this graph does have one:

Suppose a graph has a Hamilton path. What is the maximum number of vertices of degree one the graph can have? Explain why your answer is correct.

Find a graph which does not have a Hamilton path even though no vertex has degree one. Explain why your example works.

Consider the following graph:

• Find a Hamilton path. Can your path be extended to a Hamilton cycle?
• Is the graph bipartite? If so, how many vertices are in each “part”?
• Use your answer to part (b) to prove that the graph has no Hamilton cycle.
• Suppose you have a bipartite graph \(G\) in which one part has at least two more vertices than the other. Prove that \(G\) does not have a Hamilton path.

Module 4: Graph Theory

Euler and hamiltonian paths and circuits, learning outcomes.

• Determine whether a graph has an Euler path and/ or circuit
• Use Fleury’s algorithm to find an Euler circuit
• Add edges to a graph to create an Euler circuit if one doesn’t exist
• Identify whether a graph has a Hamiltonian circuit or path
• Find the optimal Hamiltonian circuit for a graph using the brute force algorithm, the nearest neighbor algorithm, and the sorted edges algorithm
• Identify a connected graph that is a spanning tree
• Use Kruskal’s algorithm to form a spanning tree, and a minimum cost spanning tree

In the next lesson, we will investigate specific kinds of paths through a graph called Euler paths and circuits. Euler paths are an optimal path through a graph. They are named after him because it was Euler who first defined them.

By counting the number of vertices of a graph, and their degree we can determine whether a graph has an Euler path or circuit. We will also learn another algorithm that will allow us to find an Euler circuit once we determine that a graph has one.

Euler Circuits

In the first section, we created a graph of the Königsberg bridges and asked whether it was possible to walk across every bridge once. Because Euler first studied this question, these types of paths are named after him.

An Euler path is a path that uses every edge in a graph with no repeats. Being a path, it does not have to return to the starting vertex.

In the graph shown below, there are several Euler paths. One such path is CABDCB. The path is shown in arrows to the right, with the order of edges numbered.

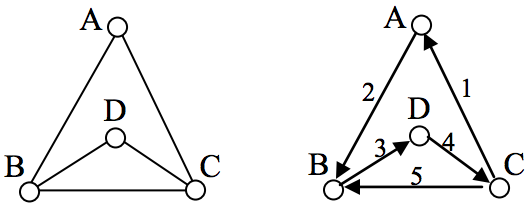
Euler Circuit

An Euler circuit is a circuit that uses every edge in a graph with no repeats. Being a circuit, it must start and end at the same vertex.

The graph below has several possible Euler circuits. Here’s a couple, starting and ending at vertex A: ADEACEFCBA and AECABCFEDA. The second is shown in arrows.

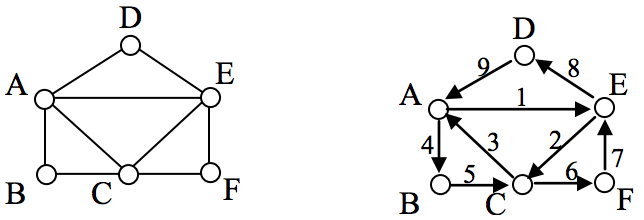
Look back at the example used for Euler paths—does that graph have an Euler circuit? A few tries will tell you no; that graph does not have an Euler circuit. When we were working with shortest paths, we were interested in the optimal path. With Euler paths and circuits, we’re primarily interested in whether an Euler path or circuit exists .

Why do we care if an Euler circuit exists? Think back to our housing development lawn inspector from the beginning of the chapter. The lawn inspector is interested in walking as little as possible. The ideal situation would be a circuit that covers every street with no repeats. That’s an Euler circuit! Luckily, Euler solved the question of whether or not an Euler path or circuit will exist.

Euler’s Path and Circuit Theorems

A graph will contain an Euler path if it contains at most two vertices of odd degree.

A graph will contain an Euler circuit if all vertices have even degree

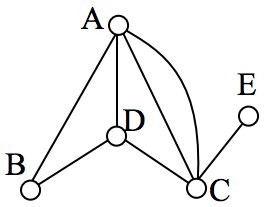
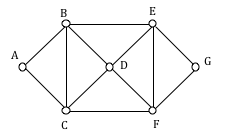
In the graph below, vertices A and C have degree 4, since there are 4 edges leading into each vertex. B is degree 2, D is degree 3, and E is degree 1. This graph contains two vertices with odd degree (D and E) and three vertices with even degree (A, B, and C), so Euler’s theorems tell us this graph has an Euler path, but not an Euler circuit.

Is there an Euler circuit on the housing development lawn inspector graph we created earlier in the chapter? All the highlighted vertices have odd degree. Since there are more than two vertices with odd degree, there are no Euler paths or Euler circuits on this graph. Unfortunately our lawn inspector will need to do some backtracking.

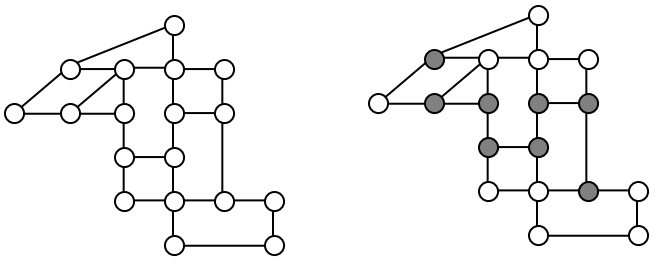
When it snows in the same housing development, the snowplow has to plow both sides of every street. For simplicity, we’ll assume the plow is out early enough that it can ignore traffic laws and drive down either side of the street in either direction. This can be visualized in the graph by drawing two edges for each street, representing the two sides of the street.

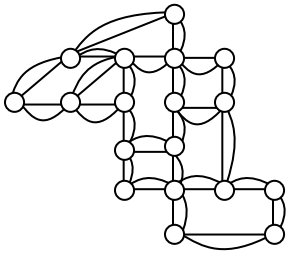
Notice that every vertex in this graph has even degree, so this graph does have an Euler circuit.

The following video gives more examples of how to determine an Euler path, and an Euler Circuit for a graph.

Fleury’s Algorithm

Fleury’s algorithm.

Find an Euler Circuit on this graph using Fleury’s algorithm, starting at vertex A.

Does the graph below have an Euler Circuit? If so, find one.

The following video presents more examples of using Fleury’s algorithm to find an Euler Circuit.

Eulerization and the Chinese Postman Problem

Not every graph has an Euler path or circuit, yet our lawn inspector still needs to do her inspections. Her goal is to minimize the amount of walking she has to do. In order to do that, she will have to duplicate some edges in the graph until an Euler circuit exists.

Eulerization

Eulerization is the process of adding edges to a graph to create an Euler circuit on a graph. To eulerize a graph, edges are duplicated to connect pairs of vertices with odd degree. Connecting two odd degree vertices increases the degree of each, giving them both even degree. When two odd degree vertices are not directly connected, we can duplicate all edges in a path connecting the two.

Note that we can only duplicate edges, not create edges where there wasn’t one before. Duplicating edges would mean walking or driving down a road twice, while creating an edge where there wasn’t one before is akin to installing a new road!

For the rectangular graph shown, three possible eulerizations are shown. Notice in each of these cases the vertices that started with odd degrees have even degrees after eulerization, allowing for an Euler circuit.

In the example above, you’ll notice that the last eulerization required duplicating seven edges, while the first two only required duplicating five edges. If we were eulerizing the graph to find a walking path, we would want the eulerization with minimal duplications. If the edges had weights representing distances or costs, then we would want to select the eulerization with the minimal total added weight.

Eulerize the graph shown, then find an Euler circuit on the eulerized graph.

Looking again at the graph for our lawn inspector from Examples 1 and 8, the vertices with odd degree are shown highlighted. With eight vertices, we will always have to duplicate at least four edges. In this case, we need to duplicate five edges since two odd degree vertices are not directly connected. Without weights we can’t be certain this is the eulerization that minimizes walking distance, but it looks pretty good.

The problem of finding the optimal eulerization is called the Chinese Postman Problem, a name given by an American in honor of the Chinese mathematician Mei-Ko Kwan who first studied the problem in 1962 while trying to find optimal delivery routes for postal carriers.  This problem is important in determining efficient routes for garbage trucks, school buses, parking meter checkers, street sweepers, and more.

Unfortunately, algorithms to solve this problem are fairly complex. Some simpler cases are considered in the exercises

The following video shows another view of finding an Eulerization of the lawn inspector problem.

Hamiltonian Circuits

The traveling salesman problem.

In the last section, we considered optimizing a walking route for a postal carrier. How is this different than the requirements of a package delivery driver? While the postal carrier needed to walk down every street (edge) to deliver the mail, the package delivery driver instead needs to visit every one of a set of delivery locations. Instead of looking for a circuit that covers every edge once, the package deliverer is interested in a circuit that visits every vertex once.

Hamiltonian Circuits and Paths

A Hamiltonian circuit is a circuit that visits every vertex once with no repeats. Being a circuit, it must start and end at the same vertex. A Hamiltonian path also visits every vertex once with no repeats, but does not have to start and end at the same vertex.

Hamiltonian circuits are named for William Rowan Hamilton who studied them in the 1800’s.

One Hamiltonian circuit is shown on the graph below. There are several other Hamiltonian circuits possible on this graph. Notice that the circuit only has to visit every vertex once; it does not need to use every edge.

This circuit could be notated by the sequence of vertices visited, starting and ending at the same vertex: ABFGCDHMLKJEA. Notice that the same circuit could be written in reverse order, or starting and ending at a different vertex.

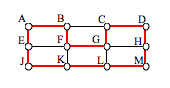
Unlike with Euler circuits, there is no nice theorem that allows us to instantly determine whether or not a Hamiltonian circuit exists for all graphs. [1]

Does a Hamiltonian path or circuit exist on the graph below?

We can see that once we travel to vertex E there is no way to leave without returning to C, so there is no possibility of a Hamiltonian circuit. If we start at vertex E we can find several Hamiltonian paths, such as ECDAB and ECABD

With Hamiltonian circuits, our focus will not be on existence, but on the question of optimization; given a graph where the edges have weights, can we find the optimal Hamiltonian circuit; the one with lowest total weight.

Watch this video to see the examples above worked out.

This problem is called the Traveling salesman problem (TSP) because the question can be framed like this: Suppose a salesman needs to give sales pitches in four cities. He looks up the airfares between each city, and puts the costs in a graph. In what order should he travel to visit each city once then return home with the lowest cost?

To answer this question of how to find the lowest cost Hamiltonian circuit, we will consider some possible approaches. The first option that might come to mind is to just try all different possible circuits.

question can be framed like this: Suppose a salesman needs to give sales pitches in four cities. He looks up the airfares between each city, and puts the costs in a graph. In what order should he travel to visit each city once then return home with the lowest cost?

Brute Force Algorithm (a.k.a. exhaustive search)

1.     List all possible Hamiltonian circuits

2.     Find the length of each circuit by adding the edge weights

3.     Select the circuit with minimal total weight.

Apply the Brute force algorithm to find the minimum cost Hamiltonian circuit on the graph below.

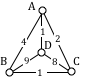
To apply the Brute force algorithm, we list all possible Hamiltonian circuits and calculate their weight:

Note: These are the unique circuits on this graph. All other possible circuits are the reverse of the listed ones or start at a different vertex, but result in the same weights.

From this we can see that the second circuit, ABDCA, is the optimal circuit.

Watch these examples worked again in the following video.

The Brute force algorithm is optimal; it will always produce the Hamiltonian circuit with minimum weight. Is it efficient? To answer that question, we need to consider how many Hamiltonian circuits a graph could have. For simplicity, let’s look at the worst-case possibility, where every vertex is connected to every other vertex. This is called a complete graph.

Suppose we had a complete graph with five vertices like the air travel graph above. From Seattle there are four cities we can visit first. From each of those, there are three choices. From each of those cities, there are two possible cities to visit next. There is then only one choice for the last city before returning home.

This can be shown visually:

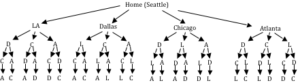
Counting the number of routes, we can see thereare [latex]4\cdot{3}\cdot{2}\cdot{1}[/latex] routes. For six cities there would be [latex]5\cdot{4}\cdot{3}\cdot{2}\cdot{1}[/latex] routes.

Number of Possible Circuits

For N vertices in a complete graph, there will be [latex](n-1)!=(n-1)(n-2)(n-3)\dots{3}\cdot{2}\cdot{1}[/latex] routes. Half of these are duplicates in reverse order, so there are [latex]\frac{(n-1)!}{2}[/latex] unique circuits.

The exclamation symbol, !, is read “factorial” and is shorthand for the product shown.

How many circuits would a complete graph with 8 vertices have?

A complete graph with 8 vertices would have = 5040 possible Hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes.

While this is a lot, it doesn’t seem unreasonably huge. But consider what happens as the number of cities increase:

As you can see the number of circuits is growing extremely quickly. If a computer looked at one billion circuits a second, it would still take almost two years to examine all the possible circuits with only 20 cities! Certainly Brute Force is not an efficient algorithm.

Nearest Neighbor Algorithm (NNA)

1.     Select a starting point.

2.     Move to the nearest unvisited vertex (the edge with smallest weight).

3.     Repeat until the circuit is complete.

Unfortunately, no one has yet found an efficient and optimal algorithm to solve the TSP, and it is very unlikely anyone ever will. Since it is not practical to use brute force to solve the problem, we turn instead to heuristic algorithms ; efficient algorithms that give approximate solutions. In other words, heuristic algorithms are fast, but may or may not produce the optimal circuit.

Consider our earlier graph, shown to the right.

Starting at vertex A, the nearest neighbor is vertex D with a weight of 1.

From D, the nearest neighbor is C, with a weight of 8.

From C, our only option is to move to vertex B, the only unvisited vertex, with a cost of 13.

From B we return to A with a weight of 4.

The resulting circuit is ADCBA with a total weight of [latex]1+8+13+4 = 26[/latex].

Watch the example worked out in the following video.

We ended up finding the worst circuit in the graph! What happened? Unfortunately, while it is very easy to implement, the NNA is a greedy algorithm, meaning it only looks at the immediate decision without considering the consequences in the future. In this case, following the edge AD forced us to use the very expensive edge BC later.

Consider again our salesman. Starting in Seattle, the nearest neighbor (cheapest flight) is to LA, at a cost of $70. From there:

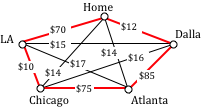
LA to Chicago: $100

Chicago to Atlanta: $75

Atlanta to Dallas: $85

Dallas to Seattle: $120

Total cost: $450

In this case, nearest neighbor did find the optimal circuit.

Watch this example worked out again in this video.

Going back to our first example, how could we improve the outcome? One option would be to redo the nearest neighbor algorithm with a different starting point to see if the result changed. Since nearest neighbor is so fast, doing it several times isn’t a big deal.

We will revisit the graph from Example 17.

Starting at vertex A resulted in a circuit with weight 26.

Starting at vertex B, the nearest neighbor circuit is BADCB with a weight of 4+1+8+13 = 26. This is the same circuit we found starting at vertex A. No better.

Starting at vertex C, the nearest neighbor circuit is CADBC with a weight of 2+1+9+13 = 25. Better!

Starting at vertex D, the nearest neighbor circuit is DACBA. Notice that this is actually the same circuit we found starting at C, just written with a different starting vertex.

The RNNA was able to produce a slightly better circuit with a weight of 25, but still not the optimal circuit in this case. Notice that even though we found the circuit by starting at vertex C, we could still write the circuit starting at A: ADBCA or ACBDA.

The table below shows the time, in milliseconds, it takes to send a packet of data between computers on a network. If data needed to be sent in sequence to each computer, then notification needed to come back to the original computer, we would be solving the TSP. The computers are labeled A-F for convenience.

a.     Find the circuit generated by the NNA starting at vertex B.

b.     Find the circuit generated by the RNNA.

While certainly better than the basic NNA, unfortunately, the RNNA is still greedy and will produce very bad results for some graphs. As an alternative, our next approach will step back and look at the “big picture” – it will select first the edges that are shortest, and then fill in the gaps.

Using the four vertex graph from earlier, we can use the Sorted Edges algorithm.

The cheapest edge is AD, with a cost of 1. We highlight that edge to mark it selected.

The next shortest edge is AC, with a weight of 2, so we highlight that edge.

For the third edge, we’d like to add AB, but that would give vertex A degree 3, which is not allowed in a Hamiltonian circuit. The next shortest edge is CD, but that edge would create a circuit ACDA that does not include vertex B, so we reject that edge. The next shortest edge is BD, so we add that edge to the graph.

We then add the last edge to complete the circuit: ACBDA with weight 25.

Notice that the algorithm did not produce the optimal circuit in this case; the optimal circuit is ACDBA with weight 23.

While the Sorted Edge algorithm overcomes some of the shortcomings of NNA, it is still only a heuristic algorithm, and does not guarantee the optimal circuit.

Your teacher’s band, Derivative Work , is doing a bar tour in Oregon. The driving distances are shown below. Plan an efficient route for your teacher to visit all the cities and return to the starting location. Use NNA starting at Portland, and then use Sorted Edges.

To see the entire table, scroll to the right

Using NNA with a large number of cities, you might find it helpful to mark off the cities as they’re visited to keep from accidently visiting them again. Looking in the row for Portland, the smallest distance is 47, to Salem. Following that idea, our circuit will be:

Portland to Salem                    47

Salem to Corvallis                   40

Corvallis to Eugene                 47

Eugene to Newport                 91

Newport to Seaside                117

Seaside to Astoria                   17

Astoria to Bend                      255

Bend to Ashland                     200

Ashland to Crater Lake           108

Crater Lake to Portland          344

Total trip length:                     1266 miles

Using Sorted Edges, you might find it helpful to draw an empty graph, perhaps by drawing vertices in a circular pattern. Adding edges to the graph as you select them will help you visualize any circuits or vertices with degree 3.

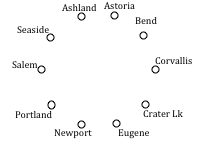
We start adding the shortest edges:

Seaside to Astoria       17 miles

Corvallis to Salem       40 miles

Portland to Salem        47 miles

Corvallis to Eugene     47 miles

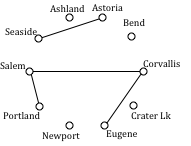
The graph after adding these edges is shown to the right.   The next shortest edge is from Corvallis to Newport at 52 miles, but adding that edge would give Corvallis degree 3.

Continuing on, we can skip over any edge pair that contains Salem or Corvallis, since they both already have degree 2.

Portland to Seaside                 78 miles

Eugene to Newport                 91 miles

Portland to Astoria                 (reject – closes circuit)

Ashland to Crater Lk  108 miles

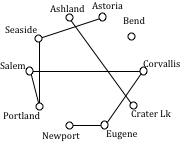
The graph after adding these edges is shown to the right. At this point, we can skip over any edge pair that contains Salem, Seaside, Eugene, Portland, or Corvallis since they already have degree 2.

Newport to Astoria                (reject – closes circuit)

Newport to Bend                    180 miles

Bend to Ashland                     200 miles

At this point the only way to complete the circuit is to add:

Crater Lk to Astoria   433 miles.  The final circuit, written to start at Portland, is:

Portland, Salem, Corvallis, Eugene, Newport, Bend, Ashland, Crater Lake, Astoria, Seaside, Portland.  Total trip length: 1241 miles.

While better than the NNA route, neither algorithm produced the optimal route. The following route can make the tour in 1069 miles:

Portland, Astoria, Seaside, Newport, Corvallis, Eugene, Ashland, Crater Lake, Bend, Salem, Portland

Watch the example of nearest neighbor algorithm for traveling from city to city using a table worked out in the video below.

In the next video we use the same table, but use sorted edges to plan the trip.

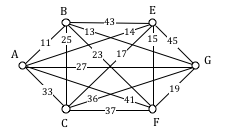
Find the circuit produced by the Sorted Edges algorithm using the graph below.

 Spanning Trees

A company requires reliable internet and phone connectivity between their five offices (named A, B, C, D, and E for simplicity) in New York, so they decide to lease dedicated lines from the phone company. The phone company will charge for each link made. The costs, in thousands of dollars per year, are shown in the graph.

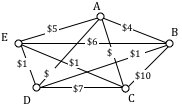
In this case, we don’t need to find a circuit, or even a specific path; all we need to do is make sure we can make a call from any office to any other. In other words, we need to be sure there is a path from any vertex to any other vertex.

Spanning Tree

A spanning tree is a connected graph using all vertices in which there are no circuits.

In other words, there is a path from any vertex to any other vertex, but no circuits.

Some examples of spanning trees are shown below. Notice there are no circuits in the trees, and it is fine to have vertices with degree higher than two.

Usually we have a starting graph to work from, like in the phone example above. In this case, we form our spanning tree by finding a subgraph – a new graph formed using all the vertices but only some of the edges from the original graph. No edges will be created where they didn’t already exist.

Of course, any random spanning tree isn’t really what we want. We want the minimum cost spanning tree (MCST) .

Minimum Cost Spanning Tree (MCST)

The minimum cost spanning tree is the spanning tree with the smallest total edge weight.

A nearest neighbor style approach doesn’t make as much sense here since we don’t need a circuit, so instead we will take an approach similar to sorted edges.

Kruskal’s Algorithm

• Select the cheapest unused edge in the graph.
• Repeat step 1, adding the cheapest unused edge, unless:
• adding the edge would create a circuit

Repeat until a spanning tree is formed

Using our phone line graph from above, begin adding edges:

AB      $4        OK

AE       $5        OK

BE       $6        reject – closes circuit ABEA

DC      $7        OK

AC      $8        OK

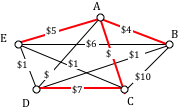
At this point we stop – every vertex is now connected, so we have formed a spanning tree with cost $24 thousand a year.

Remarkably, Kruskal’s algorithm is both optimal and efficient; we are guaranteed to always produce the optimal MCST.

The power company needs to lay updated distribution lines connecting the ten Oregon cities below to the power grid. How can they minimize the amount of new line to lay?

Using Kruskal’s algorithm, we add edges from cheapest to most expensive, rejecting any that close a circuit. We stop when the graph is connected.

Seaside to Astoria                   17 milesCorvallis to Salem                   40 miles

Portland to Salem                    47 miles

Corvallis to Eugene                 47 miles

Corvallis to Newport              52 miles

Salem to Eugene           reject – closes circuit

Portland to Seaside                 78 miles

The graph up to this point is shown below.

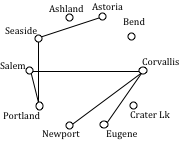
Continuing,

Newport to Salem                   reject

Corvallis to Portland               reject

Eugene to Newport                 reject

Portland to Astoria                 reject

Ashland to Crater Lk              108 miles

Eugene to Portland                  reject

Newport to Portland              reject

Newport to Seaside                reject

Salem to Seaside                      reject

Bend to Eugene                       128 miles

Bend to Salem                         reject

Astoria to Newport                reject

Salem to Astoria                     reject

Corvallis to Seaside                 reject

Portland to Bend                     reject

Astoria to Corvallis                reject

Eugene to Ashland                  178 miles

This connects the graph. The total length of cable to lay would be 695 miles.

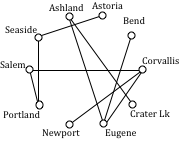
Watch the example above worked out in the following video, without a table.

Now we present the same example, with a table in the following video.

Find a minimum cost spanning tree on the graph below using Kruskal’s algorithm.

[1] There are some theorems that can be used in specific circumstances, such as Dirac’s theorem, which says that a Hamiltonian circuit must exist on a graph with n vertices if each vertex has degree n /2 or greater.

• Revision and Adaptaion. Provided by : Lumen Learning. License : CC BY: Attribution
• Learning Outcomes and Introduction. Provided by : Lumen Learning. License : CC BY: Attribution
• Graph Theory: Euler Paths and Euler Circuits . Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/5M-m62qTR-s . License : CC BY: Attribution
• Math in Society. Authored by : Lippman, David. License : CC BY: Attribution
• Graph Theory: Fleury's Algorthim . Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/vvP4Fg4r-Ns . License : CC BY: Attribution
• Hamiltonian circuits. Authored by : OCLPhase2. Located at : https://youtu.be/lUqCtywkskU . License : CC BY: Attribution
• Hamiltonian circuits . Authored by : David Lippman. Located at : https://youtu.be/SjtVuw4-1Qo . License : CC BY: Attribution
• TSP by brute force . Authored by : OCLPhase2. Located at : https://youtu.be/wDXQ6tWsJxw . License : CC BY: Attribution
• Number of circuits in a complete graph . Authored by : OCLPhase2. Located at : https://youtu.be/DwZw4t0qxuQ . License : CC BY: Attribution
• Nearest Neighbor ex2 . Authored by : OCLPhase2. Located at : https://youtu.be/3Eq36iqjGKI . License : CC BY: Attribution
• Sorted Edges ex 2 . Authored by : OCLPhase2. Located at : https://youtu.be/QxF23w3DpQc . License : CC BY: Attribution
• Kruskal's ex 1 . Authored by : OCLPhase2. Located at : https://youtu.be/gaXM0HNErc4 . License : CC BY: Attribution
• Kruskal's from a table . Authored by : OCLPhase2. Located at : https://youtu.be/Pu2_2ftkwdo . License : CC BY: Attribution

Eulerian Cycle

An Eulerian cycle, also called an Eulerian circuit, Euler circuit, Eulerian tour, or Euler tour, is a trail which starts and ends at the same graph vertex . In other words, it is a graph cycle which uses each graph edge exactly once. For technical reasons, Eulerian cycles are mathematically easier to study than are Hamiltonian cycles . An Eulerian cycle for the octahedral graph is illustrated above.

As a generalization of the Königsberg bridge problem , Euler showed (without proof) that a connected graph has an Eulerian cycle iff it has no graph vertices of odd degree .

Fleury's algorithm is an elegant, but inefficient, method of generating an Eulerian cycle. An Eulerian cycle of a graph may be found in the Wolfram Language using FindEulerianCycle [ g ].

Explore with Wolfram|Alpha

More things to try:

• acyclic graph

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Eulerian Cycle." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/EulerianCycle.html

Subject classifications

• Number System
• Linear Algebra
• Trigonometry
• Probability
• Discrete Mathematics
• Engineering Math Practice Problems

Mathematics | Euler and Hamiltonian Paths

Euler and Hamiltonian paths are fundamental concepts in graph theory, a branch of mathematics that studies the properties and applications of graphs. An Euler path visits every edge of a graph exactly once, while a Hamiltonian path visits every vertex exactly once. These paths have significant applications in various fields, including computer science, engineering, and operations research.

Table of Content

Euler Paths and Circuits

Conditions for euler paths and circuits, hamiltonian paths, hamiltonian circuit, euler and hamiltonian paths – solved examples, practice questions – euler and hamiltonian paths, applications in engineering, gate cs corner questions.

• An Euler path is a path that uses every edge of a graph exactly once .
• An Euler circuit is a circuit that uses every edge of a graph exactly once.
• An Euler path starts and ends at different vertices.
• An Euler circuit starts and ends at the same vertex.

The Konigsberg bridge problem’s graphical representation : 

• Euler Path : A connected graph has an Euler path if and only if it has exactly zero or two vertices of odd degree.
• Euler Circuit : A connected graph has an Euler circuit if and only if every vertex has an even degree.
• Hamiltonian Path : A path in a graph that visits every vertex exactly once.

Unlike Euler paths, there is no simple necessary sufficient condition for the existence of Hamiltonian paths and cycles. However, there are several theorems and heuristics:

• Dirac’s Theorem : If a graph GGG has n vertices (with n≥3n \geq 3n≥3) and every vertex has a degree of at least n/2n/2n/2, then G has a Hamiltonian cycle.
• Ore’s Theorem : If a graph GGG has n vertices and for every pair of non-adjacent vertices u and v, the sum of their degrees is at least n, then G has a Hamiltonian cycle.

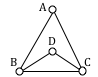
A simple circuit in a graph  [Tex]G   [/Tex] that passes through every vertex exactly once is called a Hamiltonian circuit. Unlike Euler paths and circuits, there are no simple necessary and sufficient criteria to determine if there are any Hamiltonian paths or circuits in a graph. But there are certain criteria that rule out the existence of a Hamiltonian circuit in a graph, such as if there is a vertex of degree one in a graph then it is impossible for it to have a Hamiltonian circuit.  There are certain theorems which give sufficient but not necessary conditions for the existence of Hamiltonian graphs. 

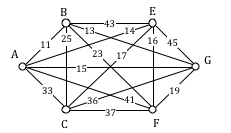
1. Determine if the following graph has an Euler circuit:

A graph with vertices {A, B, C, D} and edges {AB, BC, CD, DA, AC}

A: To have an Euler circuit, all vertices must have even degree. Degrees: A(3), B(2), C(3), D(2) Since all vertices have even degree, this graph has an Euler circuit. One possible circuit: A-B-C-D-A-C-A

2. Does the following graph have an Euler path?

A graph with vertices {P, Q, R, S} and edges {PQ, QR, RS, SP, PR}

A: For an Euler path, either all vertices have even degree, or exactly two vertices have odd degree. Degrees: P(3), Q(2), R(3), S(2) This graph has an Euler path (but not a circuit) because it has exactly two odd-degree vertices. One possible path: P-S-R-Q-P-R

3. Determine if the following graph has a Hamiltonian cycle:

A complete graph K5 with 5 vertices

A: A complete graph Kn always has a Hamiltonian cycle for n ≥ 3. So yes, K5 has a Hamiltonian cycle. One possible cycle: 1-2-3-4-5-1

4. Does the following graph have a Hamiltonian path?

A graph with vertices {A, B, C, D, E} and edges {AB, BC, CD, DE, AE, AC}

A: This graph does have a Hamiltonian path. One such path is: A-B-C-D-E

5. Given a graph G with 5 vertices, each of degree 4, determine if it has:

a) An Euler circuit

b) A Hamiltonian cycle

A: a) Yes, it has an Euler circuit because all vertices have even degree. b) Yes, it has a Hamiltonian cycle. This is a complete graph K5, which always has a Hamiltonian cycle.

6. Does the complete bipartite graph K3,3 have:

A: a) No Euler circuit. All vertices have odd degree (3). b) Yes, it has a Hamiltonian cycle. One possible cycle: 1-a-2-b-3-c-1 (where 1,2,3 are in one partition and a,b,c are in the other)

7. Consider the Petersen graph. Does it have:

A: a) No Euler circuit. All vertices have degree 3 (odd). b) No Hamiltonian cycle. The Petersen graph is a well-known example of a 3-regular graph without a Hamiltonian cycle.

8. How many edges need to be added to make an Euler circuit in a graph with 6 vertices, where 4 vertices have degree 3 and 2 vertices have degree 2?

A: To create an Euler circuit, all vertices must have even degree. We need to add 1 edge to each of the 4 vertices with degree 3. Total edges to add: 4/2 = 2 edges

9. Use Ore’s theorem to determine if this graph has a Hamiltonian cycle:

A graph with 5 vertices where the degree sum of any two non-adjacent vertices is at least 5. A: Ore’s theorem states that if the sum of degrees of any two non-adjacent vertices is ≥ n (where n is the number of vertices), then the graph has a Hamiltonian cycle. Here, n = 5, and the condition is satisfied. Therefore, this graph has a Hamiltonian cycle.

10. Apply Dirac’s theorem to determine if this graph has a Hamiltonian cycle:

A graph with 8 vertices, each having degree at least 4.

A: Dirac’s theorem states that if every vertex in a graph with n vertices (n ≥ 3) has degree ≥ n/2, then the graph has a Hamiltonian cycle. Here, n = 8, and n/2 = 4. Since each vertex has degree at least 4, Dirac’s theorem applies. Therefore, this graph has a Hamiltonian cycle.

A graph with vertices {A, B, C, D, E} and edges {AB, BC, CD, DE, EA, AC, BD}

2. Does the complete graph K6 have a Hamiltonian cycle? If so, how many distinct Hamiltonian cycles does it have?

3. For a graph G with 7 vertices, each of degree 4, determine if it has:

a) An Euler path

b) A Hamiltonian path

4. Consider the Petersen graph. How many edges need to be added to create an Euler circuit?

5. Apply Ore’s theorem to determine if this graph has a Hamiltonian cycle:

A graph with 6 vertices where the degree sum of any two non-adjacent vertices is at least 6.

6. Does the complete bipartite graph K4,3 have:

7. In a graph with 8 vertices, what’s the minimum number of edges required to guarantee the existence of a Hamiltonian cycle according to Dirac’s theorem?

8. A graph G has 10 vertices. Five vertices have degree 4, three vertices have degree 3, and two vertices have degree 5. Does G have an Euler circuit? If not, can it have an Euler path?

9. Prove or disprove: If a graph has a Hamiltonian cycle, it must also have an Euler circuit.

10. Consider a graph G with 5 vertices and 7 edges. Is it possible for G to have both an Euler circuit and a Hamiltonian cycle? Justify your answer.

1. Network Design

Hamiltonian paths and cycles are used in network design to ensure efficient routing and minimize the cost of network construction.

Example: Designing a fiber optic network that connects multiple cities with minimal cable length can be modeled as a Hamiltonian cycle problem.

2. Circuit Design

In electronic circuit design, Euler paths are used to design circuits that minimize the number of traces needed on a circuit board.

Example: Creating a circuit layout where each wire trace is used exactly once can be solved using an Euler path algorithm.

3. DNA Sequencing

Hamiltonian paths are used in bioinformatics for DNA sequencing, where the goal is to reconstruct the original sequence from overlapping fragments.

Example: Reconstructing a DNA sequence from short reads involves finding a Hamiltonian path through the overlap graph of the reads.

4. Robotics

Euler paths are used in robotics for route planning and covering every area of a space without retracing steps.

Example: Programming a robot vacuum to cover every part of a floor exactly once uses an Euler path algorithm.

5. Logistics and Routing

Hamiltonian paths and cycles are used in logistics to optimize delivery routes and minimize travel costs.

Example: Determining the most efficient route for a delivery truck to visit each customer exactly once and return to the depot can be solved using Hamiltonian cycle algorithms.

Conclusion – Euler and Hamiltonian Paths

Euler and Hamiltonian paths are essential concepts in graph theory with wide-ranging applications in network design, circuit design, DNA sequencing, robotics, and logistics. Understanding the conditions for the existence of these paths and cycles and applying appropriate algorithms can solve complex problems involving discrete structures and optimization.

FAQs on Euler and Hamiltonian Paths

What is the difference between an euler path and a hamiltonian path.

An Euler path visits every edge of a graph exactly once, while a Hamiltonian path visits every vertex of a graph exactly once.

What are the conditions for a graph to have an Euler circuit?

A graph has an Euler circuit if and only if it is connected and every vertex has an even degree.

Is there a simple condition for the existence of Hamiltonian cycles?

There is no simple necessary and sufficient condition for Hamiltonian cycles, but theorems like Dirac’s and Ore’s provide useful criteria.

How are Hamiltonian paths used in DNA sequencing?

Hamiltonian paths are used to reconstruct the original DNA sequence from overlapping fragments by finding a path through the overlap graph of the reads.

Can Euler paths be used in robotics?

Yes, Euler paths are used in robotics for route planning to cover every area of a space without retracing steps.

Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.  1. GATE CS 2007, Question 23   2. GATE CS 2005, Question 84   3. GATE CS 2008, Question 26  

Please Login to comment...

Similar reads.

• Engineering Mathematics
• graph-cycle
• How to Get a Free SSL Certificate
• Best SSL Certificates Provider in India
• Elon Musk's xAI releases Grok-2 AI assistant
• What is OpenAI SearchGPT? How it works and How to Get it?
• Content Improvement League 2024: From Good To A Great Article

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

PAK vs BAN Live Score: Hathurusinghe confident

Bangladesh head coach Chandika Hathurusinghe was confident his side could recreate their heroics from the first Test. "The morale of the players is very, very good," said former Sri Lankan batsmen Hathurusinghe. "Obviously beating Pakistan in Pakistan is not an easy task."

PAK vs BAN Live Score: Abrar Ahmed in Pak squad

The home team have recalled spinner Abrar Ahmed after going with an all-pace attack in the first Test. Former Australian pacer Gillespie admitted it will be a challenge to square the series. "We want to go out there and play positive," said Gillespie, who is in his first series with Pakistan. "It's about scoring lots of singles and with our bowling we want to be ruthless and challenging the opposition batters." But he backed under-pressure skipper Shan Masood who failed with the bat with six and 14 in the first match, and has lost all four of his Tests as captain. "Shan is a very positive captain," said Gillespie. "He wants to play and win games .... we showed that with our intent in the first game but it didn't quite work out and that's credit to our opposition. "That game is gone, but what we can do is focus on the game starting tomorrow.

PAK vs BAN Live Score: Bangladesh eye Test-series victory over Pakistan

Bangladesh are hoping to secure a first Test-series victory over Pakistan, who have left out star pacer Shaheen Shah Afridi for the second match starting in Rawalpindi on Friday. The visitors upset a normally formidable home team with a clinical ten-wicket display in the first Test -- Bangladesh's first win in over 14 encounters against Pakistan. But the hosts have been struggling through a lean spell of late, bowing out early in this year's T20 World Cup. Their last Test series was a whitewash in a three-match tour to Australia. Star pacer Afridi struggled to find his rhythm through much of the innings, with Pakistan's head coach Jason Gillespie saying he will be rested to allow him to spend time with his new-born son and family.

Hello and welcome to the Live coverage of second Test match between Pakistan and Bangladesh.