the measurement of urban travel demand

New Data and Methods for Modelling Future Urban Travel Demand: A State of the Art Review

• First Online: 29 February 2020

Cite this chapter

• Sara A. Puignau Arrigain 7 ,
• Jordi Pons-Prats 8 &
• Sergi Saurí Marchán 9  

Part of the book series: Computational Methods in Applied Sciences ((COMPUTMETHODS,volume 54))

802 Accesses

This paper aims is to provide an overview of how new data collection methods and the various advances in urban travel demand modelling are improving the understanding of mobility. These new modelling applications and data allow for a study of both new disruptive transport services and changes in travel behaviours in the “Mobility as a Service” (MaaS) context that needs to be overcome in the future.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Aditjandra PT, Cao XJ, Mulley C (2012) Understanding neighbourhood design impact on travel behaviour: an application of structural equations model to a British metropolitan data. Transp Res Part A: Policy Pract 46(1):22–32

Google Scholar  

Agatz N, Erera AL, Savelsbergh MWP, Wang X (2011) Dynamic ride-sharing: a simulation study in metro Atlanta. Procedia-Soc Behav Sci 17:532–550

Anda C, Erath A, Fourie PJ (2017) Transport modelling in the age of big data. Int J Urban Sci 21(sup1):19–42

Arentze T, Hofman F, van Mourik H, Timmermans H (2000) ALBATROSS: multiagent, rule-based model of activity pattern decisions. Transp Res Rec 1706(1):136–144

Auld J, Mohammadian AK (2012) Activity planning processes in the agent-based dynamic activity planning and travel scheduling (ADAPTS) model. Transp Res Part A: Policy Pract 46(8):1386–1403

Bahamonde-Birke FJ, Kunert U, Link H, de Dios Ortúzar J (2017) About attitudes and perceptions: finding the proper way to consider latent variables in discrete choice models. Transportation 44(3):475–493

Bao Q, Kochan B, Bellemans T, Janssens D, Wets G (2015) Investigating micro-simulation error in activity-based travel demand forecasting: a case study of the FEATHERS framework. Transp Plan Technol 38(4):425–441

Bao Q, Kochan B, Shen Y, Bellemans T, Janssens D, Wets G (2016) Activity-based travel demand modeling framework FEATHERS: sensitivity analysis with decision trees. Transp Res Rec: J Transp Res Board 89–99

Bekhor S, Dobler C, Axhausen KW (2010) Integration of activity-based with agent-based models: an example from the tel aviv model and MATSim. Arb Verk Raumplan 628

Bekhor S, Kheifits L, Sorani, M (2014) Stability analysis of activity-based models: case study of the Tel Aviv transportation model. Eur J Transp Infrastruct Res 14(4)

Ben-Akiva M, Bierlaire M (1999) Discrete choice methods and their applications to short term travel decisions. Handbook of transportation science. Springer, Berlin, pp 5–33

Ben-Akiva M, Walker J, Bernardino AT, Gopinath DA, Morikawa T, Polydoropoulou A (2002) Integration of choice and latent variable models. Perpetual motion, travel behaviour research opportunities and application challenges, pp 431–470

Berrada J, Leurent F (2017) Modeling transportation systems involving autonomous vehicles: a state of the art. Transp Res Procedia 27:215–221

Bischoff J, Nagel K (2017) Integrating explicit parking search into a transport simulation. Procedia Comput Sci 109:881–886

Bohte W, Maat K (2009) Deriving and validating trip purposes and travel modes for multi-day GPS-based travel surveys: a large-scale application in the Netherlands. Transp Res Part C: Emerg Technol 17(3):285–297

Bowman JL, Ben-Akiva ME (2001) Activity-based disaggregate travel demand model system with activity schedules. Transp Res Part A: Policy Pract 35(1):1–28

Bricka SG, Sen S, Paleti R, Bhat CR (2012) An analysis of the factors influencing differences in survey-reported and GPS-recorded trips. Transp Res Part C: Emerg Technol 21(1):67–88

Calabrese F, Diao M, Di Lorenzo G, Ferreira J Jr, Ratti C (2013) Understanding individual mobility patterns from urban sensing data: a mobile phone trace example. Transp Res Part C: Emerg Technol 26:301–313

Calabrese F, Ferrari L, Blondel Vincent D (2015) Urban sensing using mobile phone network data: a survey of research. ACM Comput Surv (CSUR) 47(2):25

Carreira R, Patrício L, Jorge RN, Magee C (2014) Understanding the travel experience and its impact on attitudes, emotions and loyalty towards the transportation provider-a quantitative study with mid-distance bus trips. Transp Policy 31:35–46

Castiglione J, Freedman J, Bradley M (2003) Systematic investigation of variability due to random simulation error in an activity-based microsimulation forecasting model. Transp Res Rec 1831(1):76–88

Castiglione J, Bradley M, Gliebe J (2015) Activity-based travel demand models: a primer

Chen C, Ma J, Susilo Y, Liu Y, Wang M (2016) The promises of big data and small data for travel behavior (aka human mobility) analysis. Transp Res Part C: Emerg Technol 68:285–299

Chorus CG, Arentze TA, Timmermans HJP (2008) A random regret-minimization model of travel choice. Transp Res Part B: Methodol 42(1):1–18

Cich G, Knapen L, Maciejewski M, Bellemans T, Janssens D et al (2017) Modeling demand responsive transport using SARL and MATSim. Procedia Comput Sci 109:1074–1079

Davis B, Dutzik T, Baxandall P (2012) Transportation and the new generation. Why young people are driving less and what it means for transportation policy. Frontier Group

de Barcelona A (2013). Pla de Mobilitat Urbana de Barcelona 2013–2018

de Dios Ortuzar J, Willumsen, LG (2011) Modal split and direct demand models. Modelling transport, 4th edn. John Wiley & Sons, New York, pp 207–225

De Oña J, De Oña R, Eboli L, Mazzulla G (2013) Perceived service quality in bus transit service: a structural equation approach. Transp Policy 29:219–226

Delbosc A, Currie G (2015) Does information and communication technology complement or replace social travel among young adults? Transp Res Rec: J Transp Res Board 76–82

Diana M, Mokhtarian PL (2009) Grouping travelers on the basis of their different car and transit levels of use. Transportation 36(4):455–467

Djavadian S, Chow JYJ (2017) An agent-based day-to-day adjustment process for modeling mobility as a service with a two-sided flexible transport market. Transp Res Part B: Methodol 104:36–57

Du Y, Zhao C, Zhang X, Sun L (2015) Microscopic simulation evaluation method on access traffic operation. Simul Model Pract Theory 53:139–148

e Silva JDA, Morency C, Goulias KG (2012) Using structural equations modeling to unravel the influence of land use patterns on travel behavior of workers in Montreal. Transp Res Part A: Policy Pract 46(8):1252–1264

Eboli L, Mazzulla G (2007) Service quality attributes affecting customer satisfaction for bus transit. J Public Transp 10(3):2

Eboli L, Mazzulla G (2010) How to capture the passengers’ point of view on a transit service through rating and choice options. Transp Rev 30(4):435–450

Fagnant DJ, Kockelman KM (2014) The travel and environmental implications of shared autonomous vehicles, using agent-based model scenarios. Transp Res Part C: Emerg Technol 40:1–13

Feng T, Timmermans HJP (2014) Extracting activity-travel diaries from GPS data: towards integrated semi-automatic imputation. Procedia Environ Sci 22:178–185

Fifer S, Rose J, Greaves S (2014) Hypothetical bias in stated choice experiments: is it a problem? And if so, how do we deal with it? Transp Res Part A: Policy Pract 61:164–177

Furuhata M, Dessouky M, Ordóñez F, Brunet M-E, Wang X, Koenig S (2013) Ridesharing: the state-of-the-art and future directions. Transp Res Part B: Methodol 57:28–46

Garikapati VM, Pendyala RM, Morris EA, Mokhtarian PL, McDonald N (2016) Activity patterns, time use, and travel of millennials: a generation in transition? Transp Rev 36(5):558–584

Ghasri M, Rashidi TH, Waller ST (2017) Developing a disaggregate travel demand system of models using data mining techniques. Transp Res Part A: Policy Pract 105:138–153

Giesecke R, Surakka T, Hakonen M (2016) Conceptualising mobility as a service. In: 2016 11th international conference on ecological vehicles and renewable energies (EVER). IEEE, pp 1–11

Group, Resource Systems (2012) The ARC and SACOG experience with activity-based models: synthesis and lessons learned. Washington, DC

Guiliano G, Hayden SA (2005) Marketing public transport. Handbooks in transport, vol 6

Gundlegård D, Rydergren C, Breyer N, Rajna B (2016) Travel demand estimation and network assignment based on cellular network data. Comput Commun 95:29–42

Habib KMN (2011) A random utility maximization (RUM) based dynamic activity scheduling model: application in weekend activity scheduling. Transportation 38(1):123–151

Hasan S, Ukkusuri SV (2014) Urban activity pattern classification using topic models from online geo-location data. Transp Res Part C: Emerg Technol 44:363–381

He Q, Head KL, Ding J (2014) Multi-modal traffic signal control with priority, signal actuation and coordination. Transp Res Part C: Emerg Technol 46:65–82

Heilig M, Mallig N, Schröder O, Kagerbauer M, Vortisch P (2018) Implementation of free-floating and station-based carsharing in an agent-based travel demand model. Travel Behav Soc 12:151–158

Huang A, Gallegos L, Lerman K (2017) Travel analytics: understanding how destination choice and business clusters are connected based on social media data. Transp Res Part C: Emerg Technol 77:245–256

Ingvardson JB, Kaplan S, Nielsen OA, Di Ciommo F, de Abreu e Silva J, Shiftan Y (2017) The Commuting habit loop: the role of satisfying existence, relatedness, and growth needs in modal choice. Technical report

Injadat M, Salo F, Nassif AB (2016) Data mining techniques in social media: a survey. Neurocomputing 214:654–670

Johansson MV, Heldt T, Johansson P (2006) The effects of attitudes and personality traits on mode choice. Transp Res Part A: Policy Pract 40(6):507–525

Jurdak R, Zhao K, Liu J, AbouJaoude M, Cameron M, Newth D (2015) Understanding human mobility from Twitter. PloS One 10(7):e0131469

Kamargianni M, Polydoropoulou A (2014) Generation Y’s travel behavior and perceptions of walkability constraints. Transp Res Rec 2430(1):59–71

Kamargianni M, Li W, Matyas M, Schäfer A (2016) A critical review of new mobility services for urban transport. Transp Res Procedia 14:3294–3303

Kaplan S, e Silva JDA, Di Ciommo F (2014) The relationship between young people’ s transit use and their perceptions of equity concepts in transit service provision. Transp Policy 36:79–87

Kelen C, Vilarino P, Christou G (2017) Advanced demand data collection technologies for multi modal strategic modelling. Transp Res Procedia 27:1058–1065

Koppelman FS, Bhat C (2006) A self instructing course in mode choice modeling: multinomial and nested logit models

Kroesen M, Handy SL (2015) Is the rise of the e-society responsible for the decline in car use by young adults? Results from the Netherlands. Transp Res Rec 2496(1):28–35

Kuflik T, Minkov E, Nocera S, Grant-Muller S, Gal-Tzur A, Shoor I (2017) Automating a framework to extract and analyse transport related social media content: the potential and the challenges. Transp Res Part C: Emerg Technol 77:275–291

Kuhnimhof T, Buehler R, Dargay J (2011) A new generation: travel trends for young Germans and Britons. Transp Res Rec 2230(1):58–67

Li Q, Liao F, Timmermans HJP, Huang H, Zhou J (2018) Incorporating free-floating car-sharing into an activity-based dynamic user equilibrium model: a demand-side model. Transp Res Part B: Methodol 107:102–123

Linares MP, Barceló J, Carmona C, Montero L (2017) Analysis and operational challenges of dynamic ride sharing demand responsive transportation models. Transp Res Procedia 21:110–129

Mans J, Interrante E, Lem L, Mueller J, Lawrence M (2012) Next generation of travel behavior: potential impacts related to household use of information and communication technology. Transp Res Rec 2323(1):90–98

Matyas MB, Kamargianni M (2017) A holistic overview of the mobility-as-a-service. In: Hungarian transport research conference

McNally MG (2000) The activity-based approachPergamon. In: Hensher DA, Button K (eds) Hand Book of Transport Modelling

Miller EJ (2017) Modeling the demand for new transportation services and technologies. Transp Res Rec 2658(1):1–7

Nourinejad M, Roorda MJ (2016) Agent based model for dynamic ridesharing. Transp Res Part C: Emerg Technol 64:117–132

Pender B, Currie G, Delbosc A, Shiwakoti N (2014) Social media use during unplanned transit network disruptions: a review of literature. Transp Rev 34(4):501–521

Petrik O, Adnan M, Basak K, Ben-Akiva M (2018) Uncertainty analysis of an activity-based microsimulation model for Singapore. Future Gener Comput Syst

Pournarakis DE, Sotiropoulos DN, Giaglis GM (2017) A computational model for mining consumer perceptions in social media. Decis Support Syst 93:98–110

Rashidi TH, Abbasi A, Maghrebi M, Hasan S, Waller TS (2017) Exploring the capacity of social media data for modelling travel behaviour: opportunities and challenges. Transp Res Part C: Emerg Technol 75:197–211

Rasouli S (2016) Uncertainty in modeling activity-travel demand in complex urban systems. TRAIL Research School

Ribeiro MD, Larrañaga AM, Arellana J, Cybis HBB (2014) Influence of GPS and self-reported data in travel demand models. Procedia-Soc Behav Sci 162:467–476

Saleem M, Västberg OB, Karlström A (2018) An activity based demand model for large scale simulations. Procedia Comput Sci 130:920–925

Shiftan Y, Ben-Akiva M (2011) A practical policy-sensitive, activity-based, travel-demand model. Ann Reg Sci 47(3):517–541

Shiftan Y, Outwater ML, Zhou Y (2008) Transit market research using structural equation modeling and attitudinal market segmentation. Transp Policy 15(3):186–195

Shiftan Y, Barlach Y, Shefer D (2015) Measuring passenger loyalty to public transport modes. J Public Transp 18(1):7

Şimşekoğlu Ö, Nordfjærn T, Rundmo T (2015) The role of attitudes, transport priorities, and car use habit for travel mode use and intentions to use public transportation in an urban Norwegian public. Transp Policy 42:113–120

Sivakumar A (2007) Modelling transport: a synthesis of transport modelling methodologies. Imperial College of London

Stathopoulos A, Cirillo C, Cherchi E, Ben-Elia E, Li Y-T, Schmöcker J-D (2017) Innovation adoption modeling in transportation: new models and data. J Choice Model

Stock K (2018) Mining location from social media: a systematic review. Comput Environ Urban Syst

Tan W, Chai Y, Wang W, Liu Y (2012) General modeling and simulation for enterprise operational decision-making problem: a policy-combination perspective. Simul Model Pract Theory 21(1):1–20

Tyrinopoulos Y, Aifadopoulou G (2008) A complete methodology for the quality control of passenger services in the public transport business. Eur Transp 38(38):1–16

Van Acker V, Mokhtarian PL, Witlox F (2014) Car availability explained by the structural relationships between lifestyles, residential location, and underlying residential and travel attitudes. Transp Policy 35:88–99

Van Lierop D, El-Geneidy A (2016) Enjoying loyalty: the relationship between service quality, customer satisfaction, and behavioral intentions in public transit. Res Transp Econ 59:50–59

Van Wee B (2002) Land use and transport: research and policy challenges. J Transp Geogr 10(4):259–271

Veldhuisen J, Timmermans H, Kapoen L (2000) Microsimulation model of activity-travel patterns and traffic flows: specification, validation tests, and Monte Carlo error. Transp Res Rec: J Transp Res Board 126–135

Wang Y, Szeto WY, Han K, Friesz TL (2018) Dynamic traffic assignment: a review of the methodological advances for environmentally sustainable road transportation applications. Transp Res Part B: Methodol

Wegener M (2013) The future of mobility in cities: challenges for urban modelling. Transp Policy 29:275–282

Wismans L, De Romph E, Friso K, Zantema K (2014) Real time traffic models, decision support for traffic management. Procedia Environ Sci 22:220–235

Xiong Y, Zhang J (2016) Effects of land use and transport on young adults’ quality of life. Travel Behav Soc 5:37–47

Ye R, Titheridge H (2017) Satisfaction with the commute: the role of travel mode choice, built environment and attitudes. Transp Res Part D: Transp Environ 52:535–547

Zhang J, Chikaraishi M, Xiong Y, Jiang Y, Seya H (2016) Young people’s life choices and travel behavior: state-of-the-art and future perspectives. In: A discussion paper for the workshop ‘Young People’s Life Choices and Travel...’

Zheng H, Son Y-J, Chiu Y-C, Head L, Feng Y, Xi H, Kim S, Hickman M, et al (2013) A primer for agent-based simulation and modeling in transportation applications. Technical report, United States, Federal Highway Administration

Zhuge C, Shao C, Wang S, Hu Y (2019) Sensitivity analysis of integrated activity-based model: using MATSim as an example. Transp Lett 11(2):93–103

Download references

Author information

Authors and affiliations.

Campus Nord UPC Jordi Girona, 1-3 Building C-3, 08034, Barcelona, Spain

Sara A. Puignau Arrigain

CIMNE Castelldefels Edifici C3 Parc Mediterrani de la Tecnología UPC C/ Esteve Terrades no 5, 08860, Castelldefels, Spain

Jordi Pons-Prats

CENIT, Barcelona, c/Jordi Girona s/n Campus Nord UPC, Edifici C1, 08034, Barcelona, Spain

Sergi Saurí Marchán

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Sara A. Puignau Arrigain .

Editor information

Editors and affiliations.

International Center for Numerical Methods in Engineering, CIMNE, Universidad Politecnica Catalunya, Barcelona, Spain

Faculty of Information Technology, University of Jyväskylä, Jyväskylä, Finland

Pekka Neittaanmäki

International Center for Numerical Methods in Engineering, CIMNE, Universitat Politècnica de Cataluny, Barcelona, Spain

Jacques Periaux

Tero Tuovinen

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this chapter

Puignau Arrigain, S.A., Pons-Prats, J., Saurí Marchán, S. (2020). New Data and Methods for Modelling Future Urban Travel Demand: A State of the Art Review. In: Diez, P., Neittaanmäki, P., Periaux, J., Tuovinen, T., Pons-Prats, J. (eds) Computation and Big Data for Transport. Computational Methods in Applied Sciences, vol 54. Springer, Cham. https://doi.org/10.1007/978-3-030-37752-6_4

Download citation

DOI : https://doi.org/10.1007/978-3-030-37752-6_4

Published : 29 February 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-37751-9

Online ISBN : 978-3-030-37752-6

eBook Packages : Engineering Engineering (R0)

THE MEASUREMENT OF URBAN TRAVEL DEMAND

No abstract provided.

• Find a library where document is available. Order URL: http://worldcat.org/issn/00472727
• DANIEL MCFADDEN INCLUDES BIBLIOGRAPHICAL REFERENCES
• McFadden, D
• Publication Date: 1974
• Pagination: p. 303-328
• Journal of Public Economics
• Publisher: Elsevier
• ISSN: 0047-2727

Subject/Index Terms

• TRT Terms: Mathematical models ; Mode choice

Filing Info

• Accession Number: 00404312
• Record Type: Publication
• Source Agency: UC Berkeley Transportation Library
• Files: TLIB
• Created Date: Oct 31 1985 12:00AM

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 17 April 2023

Interrelationships between urban travel demand and electricity consumption: a deep learning approach

• Ali Movahedi   ORCID: orcid.org/0000-0001-8685-2965 1 ,
• Amir Bahador Parsa 1 ,
• Anton Rozhkov 2 ,
• Dongwoo Lee 3 ,
• Abolfazl Kouros Mohammadian   ORCID: orcid.org/0000-0003-3595-3664 1 &
• Sybil Derrible   ORCID: orcid.org/0000-0002-2939-6016 1 , 4  

Scientific Reports volume  13 , Article number:  6223 ( 2023 ) Cite this article

1652 Accesses

8 Citations

5 Altmetric

Metrics details

• Civil engineering
• Computer science

The analysis of infrastructure use data in relation to other components of the infrastructure can help better understand the interrelationships between infrastructures to eventually enhance their sustainability and resilience. In this study, we focus on electricity consumption and travel demand. In short, the premise is that when people are in buildings consuming electricity, they are not generating traffic on roads, and vice versa, hence the presence of interrelationships. We use Long Short Term Memory (LSTM) networks to model electricity consumption patterns of zip codes based on the traffic volume of the same zip code and nearby zip codes. For this, we merge two datasets for November 2017 in Chicago: (1) aggregated electricity use data in 30-min intervals within the city of Chicago and (2) traffic volume data captured on the Chicago expressway network. Four analyses are conducted to identify interrelationships: (a) correlation between two time series, (b) temporal relationships, (c) spatial relationships, and (d) prediction of electricity consumption based on the total traffic volume. Overall, from over 250 models, we identify and discuss complex interrelationships between travel demand and electricity consumption. We also analyze and discuss how and why model performance varies across Chicago.

Similar content being viewed by others

Systematic review and meta-analysis of ex-post evaluations on the effectiveness of carbon pricing

Urbanization and regional climate change-linked warming of Indian cities

The role of artificial intelligence in achieving the Sustainable Development Goals

Introduction.

The analysis of infrastructure use data in relation to other components of the infrastructure can help better understand interdependencies and interrelationships between them, with the potential to enhance their sustainability and resilience. Indeed, no infrastructure system works in isolation. All infrastructure systems—including transport, water, wastewater, electricity, gas, and telecommunications—are interdependent 1 , 2 . In part because of these interdependencies, but also intrinsic to how people live, the way infrastructure systems are used is also interrelated. For example, Movahedi and Derrible 3 showed that electricity, gas, and water consumption in large-scale buildings are interrelated (i.e., the consumption of one can be predicted by the two others). Zhang and Qian 4 classified the patterns of electricity consumption over a night to estimate the traffic congestion of a highway in the morning. Overall, infrastructure systems are often more interrelated than initially expected, for example by sharing physical surface and subsurface space 5 and by competing for time and resources 6 , 7 .

In this study, by using zip code-level electricity data as well as traffic loop detector data, we seek to identify and understand interrelationships between travel demand and electricity demand. More precisely, using traffic data to count the number of vehicles entering and exiting a zip code can capture the number of people in a zip code at a given time who may be in buildings otherwise, consuming electricity. Concurrently, a decrease in electricity consumption can express that people have left a building and may use a vehicle, generating traffic. In this study, we use electricity consumption data of several zip codes in Chicago at 30-min intervals for November 2017. To achieve our goal, we use Long Short Term Memory (LSTM) network—a type of deep learning model—to model electricity consumption patterns of zip codes based on the traffic volume of the same zip code and nearby zip codes. The specific objectives of the study are to:

Understand the correlation between electricity consumption and traffic volume.

Investigate the temporal relationships between electricity consumption and traffic volume.

Investigate the spatial relationships between electricity consumption and traffic volume.

Develop models to predict electricity consumption based on traffic volume.

In the next section, we review the literature on electricity consumption and traffic modeling, and on interrelationships between infrastructure systems in cities. After, we describe the electricity consumption and traffic datasets used in the study. Next, we go over the results by addressing each objective sequentially, and we then discuss these results. Finally, we explain in detail the methodological approach utilized in the study.

Literature review

The electricity power grid is a complex system with many components 8 . The stable and uninterrupted operation of the power grid plays a vital role in economic development, national security, and overall social welfare. As of this writing, electricity cannot be cheaply and effectively stored in required massive amounts. As a result, electric utilities and other power market players must forecast electricity consumption in the (a) short-term (few minutes to hours), (b) mid-term (hours to a day ahead), and (c) long-term (seasonal/annual, up to a few years) in generation, transmission, and distribution networks. Thanks to the deployment of smart meters, predictions have become generally more accurate. This accurate forecasting of electricity consumption levels is crucial for power systems, and the selected method for making predictions provides a better understanding of the dynamics of the system and can even help ease operating costs for market players. The traditional predictive techniques include the construction of mathematical and statistical models such as auto-regressive and moving average (ARMA) models 9 ; auto-regressive integrated moving average (ARIMA) models 10 ; multiple linear regression (MLR) and principal component analysis (PCA) models 11 ; gray models (GM) 12 ; and Kalman filter-based (KF) models 13 . Nonetheless, traditional statistical models are known to be limited. For instance, GM models are not always effective for electrical load forecasting but work better for addressing small sample problems 14 and ARMA models may fail to consider the influence of random variables other than in typical time series forecasting methods 10 , 14 . This means that traditional statistical models work well in normal daily conditions, but they become less reliable while dealing with meteorological, sociological, and economic changes 15 or with relations to other systems.

To deal with complex nonlinear relationships, machine learning (ML) and deep learning techniques are generally preferred. The following techniques are mentioned in the literature: artificial neural networks (ANN) 16 , 17 , 18 fuzzy-logic-based algorithms 19 , 20 , genetic-algorithm-based (GA) neural network 21 , support vector machine (SVM) 22 , tree-based models 23 , 24 , 25 , LSTM-based neural network 26 ; single hidden layer network configurations with random weights (RWSLFN) 27 , and multilayer perceptron (MLP) 28 to name a few. In the literature, LSTM has been shown to perform particularly well on time series data for a range of applications, including to predict the spread of COVID-19 29 , 30 , 31 , 32 . Specifically looking at traffic forecasting and flow prediction, several studies 33 , 34 also found that LSTM performed better than traditional techniques like ARIMA or other ML techniques like support vector regression (SVR). In this study, we have opted to solely use LSTM as our main goal is not to find the best performing model but to investigate the presence of interrelationships between electricity consumption and traffic volume.

As many studies demonstrate 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44 , 45 , 46 , 47 , 48 , 49 , 50 , 51 , electricity consumption is linked to myriads of variables, from urban characteristics (e.g., morphology, density) and building characteristics (e.g., size and insulation technology) to weather characteristics (e.g., temperature and cloud coverage) and socio-economic and demographic characteristics (e.g., household income and age). Yet, this list is not exhaustive. As infrastructure systems are interdependent and interrelated by nature 52 , electricity consumption is also linked to demand patterns for other infrastructure services, such as residents commute time, traffic, and urban mobility patterns, suggesting that traffic network data can be used as a source of information to predict electricity consumption as well 53 . To date, little research has been carried out and not many studies are available that focus on the interrelation between travel and electricity demand. Few studies explore the causal interdependencies between electricity, transport, and weather data 53 , 54 . Gilanifar et al. 55 developed a Bayesian Gaussian Process model that explores usage of electricity to enhance short-term load forecasting. Aparicio et al. 56 studied the dependencies between power demand and road traffic data using linear correlation and compare the results with other standard features, such as historical load and temperature.

Electricity

In this article, we work with anonymized energy usage data in 30-min intervals at the zip code level within the city of Chicago collected by the local utility Commonwealth Edison (ComEd) and accessible (for a fee) 57 . Each measurement in the dataset represents the total electricity consumed (in kWh) for a specific customer in a certain time interval (30 min). We decided to build our research on this dataset because we assume that the raw high-resolution interval data that we get directly from the automated metering infrastructure (AMI) have a high level of accuracy and fidelity.

Interval data from AMI has become widely available to utilities throughout the U.S. 58 . It is often used to identify energy use trends and peaks in the interest of anomaly detection 59 and to make predictions of electricity consumption 60 to improve the stability of the power grid. Household data include load shapes measured at the household level considers seasonal and daily fluctuations and show significant differences in electricity consumption during the day, week, month, and year. We are interested in observing the loads in one month with a specific focus on the time of the day and the day of the week. We used residential electricity consumption from 28 zip codes located along the main transport corridors of Chicago: I-290, I-90, I-55, I-57, and I-94 interstate expressways for the month of November 2017.

While beneficial for both utilities and customers, data collected and utilized using AMI systems have caused concerns regarding customers’ privacy 61 . Although Martínez et al. 62 observes a potential privacy issue of simple anonymization methods, the distribution of fine-grained data is normally considered acceptable as long as they cannot be linked to the households they originate from through an anonymization process 63 .

In this study, we use data that consists of fine-grained records of electricity consumption aggregated by 5-digit zip codes where specific identifiers, including but not limited to name, address, and electric account number, are omitted. Table 1 shows average electricity consumption per building in each zip code (in kWh). The table also includes area (in square kilometers) and population (based in American Community Survey (ACS) 2019 5-Year Data) for each zip code for the interest of the reader.

Traffic volume is captured by loop detectors on the Chicago expressway network. These data are collected by the Gateway Traveler Information System and provided by the Illinois Department of Transportation (IDOT). For this study, 211 loop detectors across Chicago from the Kennedy (I-90/94), Eden (I-94), Eisenhower (I-290), Stevenson (I-55), Dan Ryan (I-90/94), Bishop Ford (I-94), and I-57 expressways are used. Each loop detector includes the number of cars that pass a point in the last 5 min. Standard data cleaning processes were applied to remove missing and erroneous data points that may originate from detector malfunction, pavement condition, or from any other reason. Finally, we aggregated traffic volumes to 30-min time periods to be able to merge the traffic dataset with the electricity consumption dataset. Table 2 shows the average traffic volume per lane per 5 min in each zip code across Chicago. Similar to Table 1 , we added the area and population for each zip code. In this study, we only focus on 28 zip codes (out of 56 in Chicago) because the expressway system only cross 28 zip codes.

Correlation between electricity consumption and traffic volume

First, we can look at the correlation between two time-series datasets, traffic volume and electricity consumption. For that, we utilize the Pearson r correlation coefficient to measure the linear relation between electricity consumption and traffic volume. Specifically, we calculate the Pearson coefficients in three levels: loop detector, zip code, and citywide.

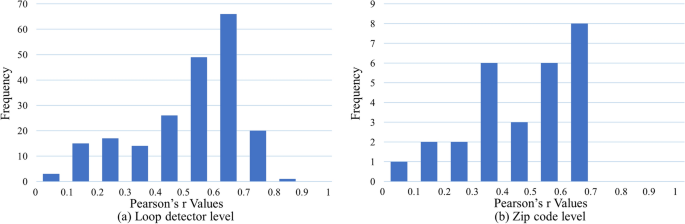
For each loop detector, we assign the zip code in which the loop detector is located. Then, we calculate the Pearson r value for each loop detector across the city. Figure  1 a shows the histogram of the Pearson r values. They are distributed between 0.004 and 0.81. The highest frequency of Pearson r values (66 out of total 211 loop detectors) is in the range [0.6, 0.7). To interpret properly the Pearson results we need to consider where zip codes with similar Pearson r values are located. Figure  2 shows the Pearson r values of the loop detectors and zip codes on a Chicago map. We can see that most loop detectors and zip codes with similar Pearson r values are located near one another.

Pearson r values.

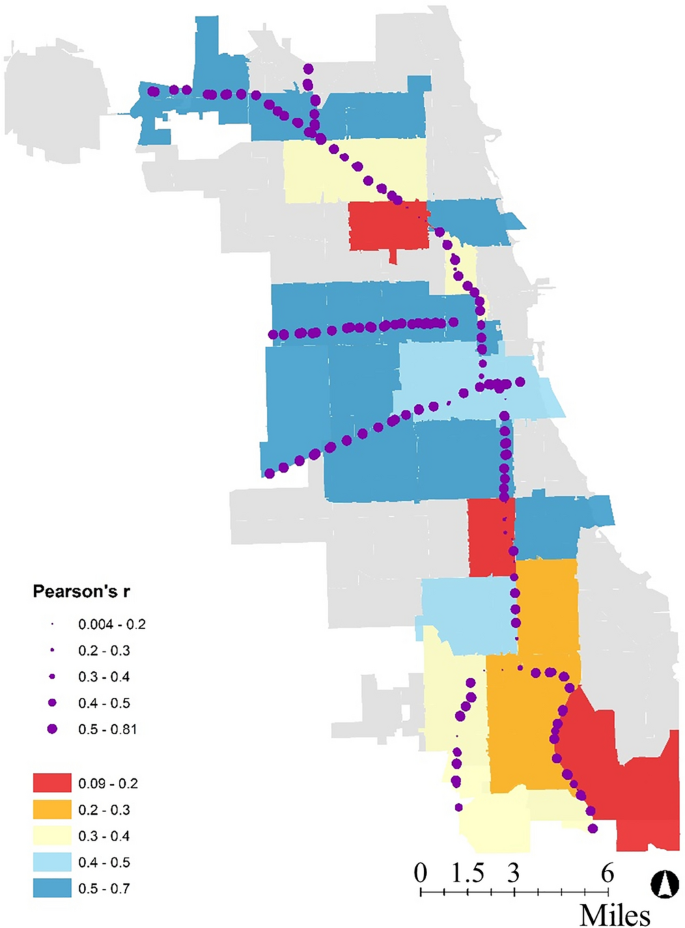
Pearson's r values—Chicago map. Environmental Systems Research Institute (Esri) ArcGIS Desktop 10.8.1 commercial versions were used to perform preliminary data preparation and convert tabular data to spatial data. URL: https://www.esri.com/en-us/arcgis/products/arcgis-desktop/resources .

At the zip code level, we consider all loop detectors in one zip code and calculate the Pearson r values for electricity consumption and traffic volume. Figure  1 b shows that Pearson r values are distributed between 0.09 and 0.66 with eight values being in the range [0.6, 0.7). Figure  2 shows how different zip codes have different correlations between electricity consumption and traffic volume. Except for a few zip codes, the figure suggests that the correlation is higher in the north side and the center of the city, and it decreases as we move south. This difference likely stems from the fact that expressways are used as the boundary between zip codes in the south. On a map, while individual loop detectors belong to one zip code, the drivers getting off the expressway may be going to the adjoining zip code. The low accuracy values therefore do not necessarily suggest the absence of interrelationships, but the lack adequate data.

At the citywide level, we use all the traffic volume data and the corresponding electricity consumption of the zip codes to calculate the overall Pearson r value for Chicago that comes to 0.14. Next, we consider a delay in the datasets since a person leaving a building can take time before reaching an expressway and vice versa. Specifically, we increase the delay from 30 min to one day in 30-miniute increments (i.e., 30 min, 60 min, 90 min, …, 1 day) and calculate the correlation of the electricity consumption with the delayed traffic volume. The result of the overall Pearson coefficient correlation shows that the 60 min delay has the highest Pearson value with 0.16, which is low and does not suggest strong correlations at the citywide level.

Temporal relationships

The goal of this section is to investigate the temporal relationships between traffic volume and electricity consumption. For that, we train LSTM models using traffic volume to predict electricity consumption in a zip code. The first question that arises is the size of the time window that should be used. For example, if we want to predict electricity consumption of a zip code at 4:00 PM, is using traffic volume at 4:00 PM in nearby loop detectors sufficient? Or is it better to consider two time windows with traffic volumes at 3:30 PM and 4:00 PM together to predict the electricity consumption at 4:00 PM? Or is it better to consider more time windows, like 16 from 8:30 AM to 4:00 PM?

To answer this question, we test many time windows for each zip code and compare the performance of the model. Specifically, to predict electricity consumption at time t , first we use traffic volume at time t and train and assess the performance of the trained LSTM model. Then we use traffic volumes at times t and t  −  30 min and perform the same analysis. The same procedure is repeated until 24 30-min periods are tested, representing a 12-h time window.

The results can be categorized into two groups. In group 1, increasing the time window steadily increases the model performance; Fig.  3 shows an example for zip code 60631. In group 2, increasing the time window initially increases the model performance, but only up to a point (around 16 time periods or 8 h); Fig.  3 shows an example for zip code 60616.

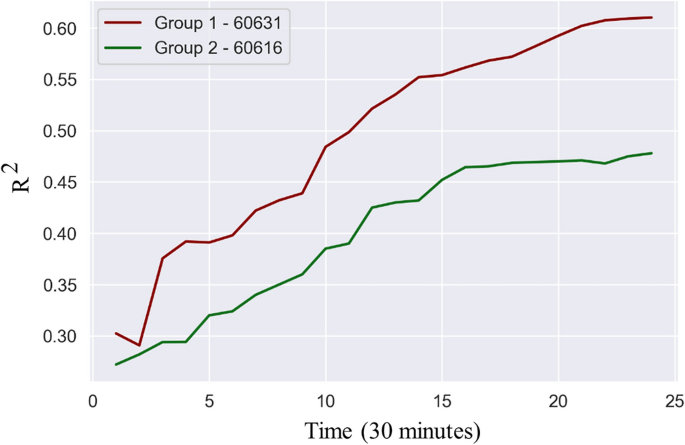
Temporal interrelationships.

While every zip code has a specific optimal time window, a time window of 16 periods (8 h) tends to perform well across all zip codes since it shows both a high performance for groups 1 and 2 zip codes.

These results are interesting and suggest that the temporal interrelationships between electricity use and travel demand are complex. In particular, we expected the optimal time window to be around 2–3 h for every zip code, to take into account typical rush hour periods, but we find that accuracy keeps increasing until at least 8 h. This means that to predict electricity consumption at 5PM, the use of traffic data between 9AM and 5PM is preferred. We posit that a larger time window of 8 h better captures lifestyle elements, such as an 8-h workday, but this value could vary across by culture.

Spatial relationships

The goal of this section is to investigate the impact of the distance between zip codes and loop detectors on the relationships between electricity consumption and traffic volume. Therefore, in this section, first, we train LSTM models to predict electricity consumption based on the traffic data from the closest loop detectors, then we increase the distance between loop detectors and the zip code. Here, we use an 8-h time window in our LSTM models (as found preferable in the previous section). To choose the zip codes to study the spatial relationships, we consider four conditions to control the impact of traffic volume from one expressway on the electricity consumption of a zip code. First the zip code should be crossed by only one expressway. Second, there should be only the loop detectors from the same expressway and no other loop detectors from other expressways in a radius of 5 km to limit the amount of noise fed to the model. Third, the zip code should be far enough from the boundaries of Chicago so we can have loop detectors on both side of the zip codes. Fourth, the accuracy of the LSTM model should be significantly more than zero to suggest the existence of a relationship. We applied these four conditions on the Chicago map and few zip codes satisfied them. As an example, we select three zip codes to study the relationships between electricity and travel demand.

To investigate the spatial relationship, we select one set of loop detectors that cross the zip code; each set has one loop detector in one direction of the expressway (toward the zip code) and one in the other direction (away from the zip code). The initial set is the ones closest to the centroid of the zip code. Then, we increase the distance and consider two new loop detectors further away from the centroid of the zip code. The procedure is repeated several times to loop detectors further away on the same expressway. Each time, a model is trained and the performance is compared.

Figure  4 shows the accuracy and errors of the models in terms of R 2 , MAE, and RMSE. In Fig.  4 a,b, the average distance between the set of loop detectors (one for each direction) and the centroid of the corresponding zone is shown on the x-axis.

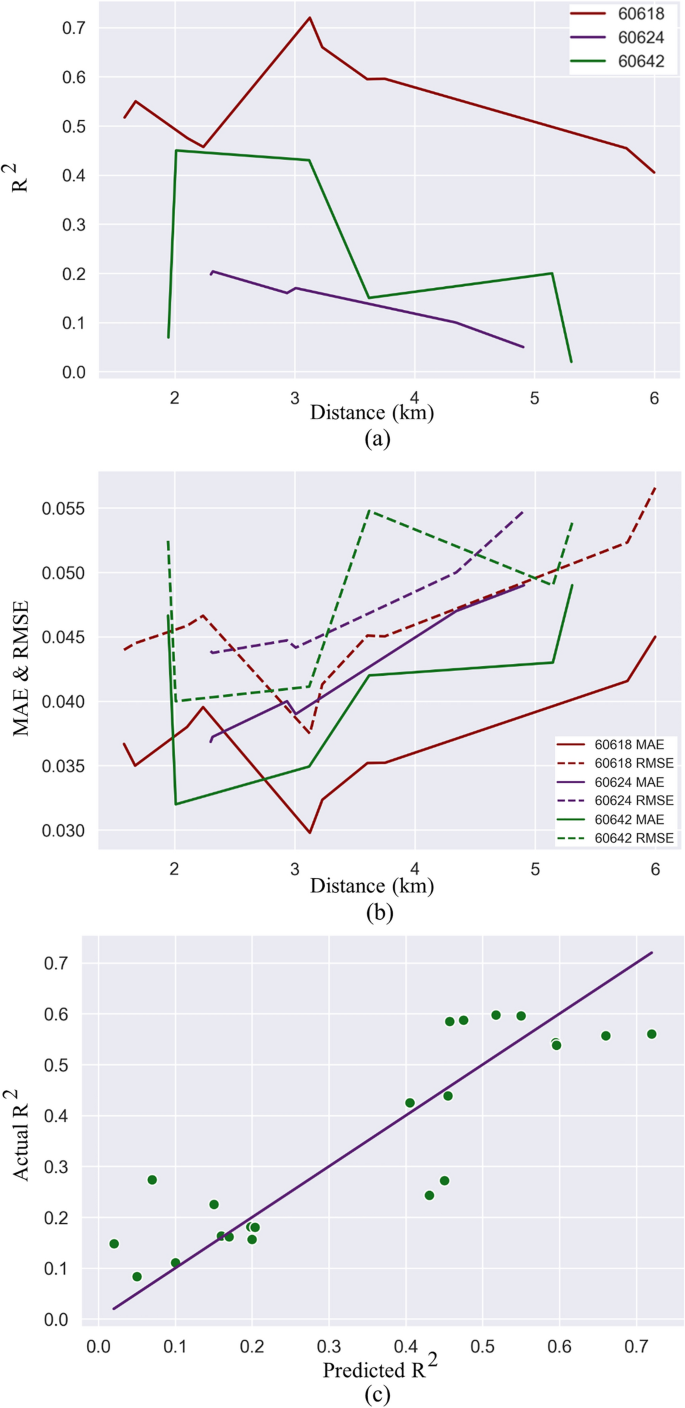
Spatial relationships between electricity consumption and travel demand.

The purple line in Fig.  4 a shows the spatial relationship found in zip code 60624. Here, increasing the distance between loop detectors and zip code reduces the accuracy and increases the MAE and RMSE. As expected, increasing the distance reduces the relationships between electricity consumption and traffic volume in this case.

Second, the dark red line in Fig.  4 a is for zip code 60618. There, we observe that by increasing the distance, the model accuracy first increases and then it decreases after a certain distance. This phenomenon was unexpected since it suggests that loop detectors located in other zip codes are better able to predict electricity consumption. To further analyze the spatial relationships, we can use all loop detectors in the same zip code to predict the electricity consumption, which we present in the next section.

Finally, the green line in Fig.  4 a shows the third type of spatial relationship. Here, increasing distance has no straightforward impact on the model performance.

Overall, we find that complex and unobvious relationships can exist between electricity consumption and traffic volume. Nonetheless, we should consider that each zip code has its own attributes, and to capture these attributes we can include a zip-code level fixed effect as is common in econometrics. Fixed effect variables are used to capture unique features of a data point despite the presence of common attributes 63 . What we can do here is to express R 2 values as a function of distance from the zip code centroid. But because electricity consumption is collected at the zip code level—a surface area in square kilometers—we should use the square of the distance in our model instead. Our model therefore becomes:

where RSquared ij is the accuracy of model i in zip code j , \({distance}_{ij}\) is the distance between loop detectors and the zip code centroid in the model i in zip code j , \({zc}_{j}\) is the zip code fixed effect to distinguish between zip codes, \({\varepsilon }_{ij}\) is the error term, and \({a}_{0}\) is the constant term.

The result of the regression is as follows \({a}_{0}=0.293\) and \({a}_{1}=-0.0052\) with a p-value of 0.04, and the zip code fixed effect values are 0.317 for zip code 60618 and − 0.085 for 60624 (note that since we have three zip codes, we have two fixed effect values for the zip codes). The R 2 of the general fit is 0.78. Figure  4 c shows the actual versus predicted values of R 2 using Eq. ( 1 ) and the coefficient values that we calculated. We find a negative relationship with the value of 0.0052 between distance squared and R 2 values. In other words, we find that increasing the squared distance by one square kilometer generally decreases the accuracy of the model by 0.0052. An ANOVA test is also performed to test the null hypothesis (i.e., whether all variables could be statistically zero). Table 3 shows the result of the ANOVA test. Because the value of the F statistic is 21.77, which is greater than F(3, 18) = 2.416, the null hypothesis can be rejected with a 99% confidence level.

Overall, despite a careful selection of zip codes, we can see that the spatial relationship between traffic volume and electricity consumption are also complex, but they exist. More work is needed to gain a better understanding of these relationships.

Prediction models across the city

Here, we train two sets of models. The first set of models uses all loop detectors in a zip code to predict the electricity consumption of the zip code. The second set of models uses single loop detectors to predict electricity consumption of the zip code in which they are located.

In the first set of models, we develop 28 LSTM models for the 28 zip codes that are crossed by at least one expressway in Chicago. The input of the models is 8 h of traffic volume collected by all loop detectors in a zip code (8 h is selected since it performed well across all zip codes in the temporal interrelationships section). The output is the average electricity consumption of the zip code at the end of the 8-h period.

Figure  5 a shows maps of Chicago with the R 2 , MAE, and RMSE values of the 28 LSTM models. First, we can see the overall performance of the models are better in the north side of Chicago than the south side. As mentioned above, one problem we face with the south side of Chicago is that the expressway serves as a boundary between zip codes. It is therefore more difficult to determine whether drivers exiting the expressway stay in the zip code where the loop detector is located or whether they go to the adjoining zip code.

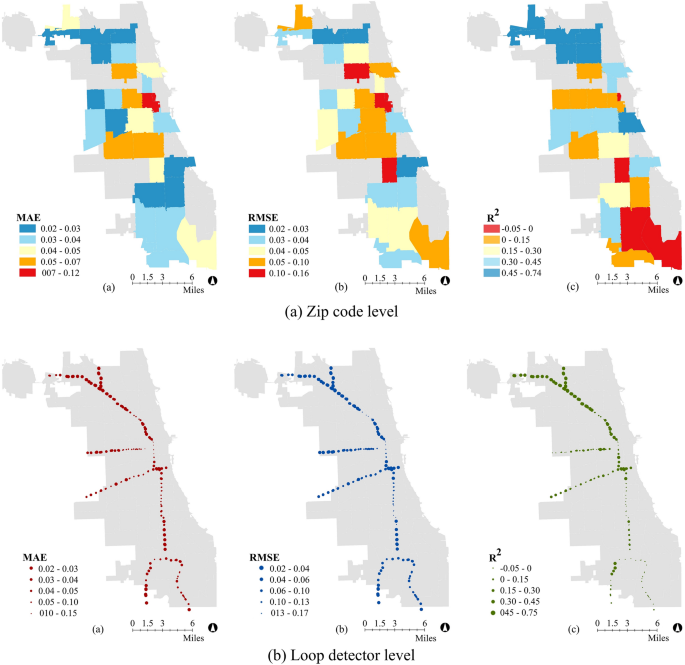
Performance of zip code and loop detector level models that use traffic volume to predict electricity consumption. Environmental Systems Research Institute (Esri) ArcGIS Desktop 10.8.1 commercial versions were used to perform preliminary data preparation and convert tabular data to spatial data. URL: https://www.esri.com/en-us/arcgis/products/arcgis-desktop/resources .

In the second set of models, we train 211 LSTM models for the 211 loop detectors in Chicago to predict the electricity consumption of the zip code to which each loop detector belongs. For each model, R 2 , MAE, and RMSE are calculated and shown in Fig.  5 b; larger circles represent higher accuracies. We can see that accuracies are higher in the north side, similar to the previous models, likely again because the expressways serve as a boundary between zip codes in the south.

Overall, these results suggest that electricity demand and travel demand are interrelated, as in, one is related to the other and vice versa, but these interrelationships can be complex.

Interestingly, we note that the model performances are similar whether all or single loop detector are selected. This result suggest that single loop detectors may be sufficient to capture relationships between travel demand and electricity consumption. Another future area of research could focus on how much data is needed to capture interrelationships between infrastructure systems.

The results show that the correlation between electricity consumption and traffic volume is complex since it varies by zip code across Chicago with Pearson values ranging between 0.04 and 0.81. Second, the optimum time window to analyze the temporal interrelationship between electricity consumption and traffic volume is 8 h. Furthermore, we investigated the spatial relationship between electricity consumption and travel demand. Despite finding complex and unobvious relationships, we detected a global linear relationship between distance squared and R 2 values; specifically, that increasing the squared distance by one square kilometer decreases the accuracy of the model by 0.0052. Finally, we developed 239 LSTM models to predict electricity consumption of a zip code using traffic volume from the same zip code and found a range of model performance across the city.

Overall, the idea of the study is novel. The articles listed in the literature review section explore various methods for short-term load forecasting and related applications in the field of energy and transport. While they also discuss applications of these methods in energy management, travel mode choice modeling, and accident detection, none of them explore the spatial relationship between electricity consumption and travel demand. As our study is novel, it cannot be compared with other articles. Nevertheless, we recognize that the interrelationships between traffic volume and electricity consumption are likely influenced by a range of complex and context-specific factors from obvious factors like the presence of alternate travel modes (e.g., transit, walk, bike) to less obvious factors related to household characterisitcs 13 , and daily 10 and seasonal 12 effects.

Furthermore, this study has several limitations. In particular, it would have benefited from having access to origin–destination data (not for a typical date but for a specific day to compare energy use patterns) and to more detailed travel volume data (beyond traffic volumes on the expressway system).

In terms of policy implications, this work suggests that policies made to impact one infrastructure system can impact others. For example, many cities have adopted time-varying pricing practices for tollways (e.g., Singapore) and public transport (e.g., Washington DC) to encourage people to avoid rush hour periods and lessen congestion, which must have an impact of electricity consumption (as well as other resources such as water and gas). With the global push toward infrastructure decentralization and distribution 65 , we recommend better coordination among utilities and transport service providers.

Future work should focus on further understanding these interrelationships, ideally using other more spatially disaggregate datasets. It is aligned with limitations from other research 25 , which uses a similar methodology and mentions that the exploration of many datasets from distant energy contexts is necessary for a broader understanding of the problem. Another future area of research is on how much data is needed to capture interrelationships between infrastructure systems. For instance, increasing the spatial resolution of the data by collecting information at a more disaggregated level, as well as incorporating data on public transportation usage and other mobility-related variables, could further provide additional insights and improve the accuracy of models.

Material and methods

Long short-term memory (lstm).

Neural Networks (NN) are one of the most widely used types of machine learning techniques. They are made of three layers: (a) input, (b) output, and (c) hidden. The most common types of NN have a cost function, and the goal is to minimize this cost function through re-adjusting the weights (i.e., model parameters) using a backpropagation technique. Recurrent Neural Networks (RNN) are more advanced and complex models that belong to the family of deep learning techniques. In RNN, a temporal loop connects the hidden layer to itself, meaning that the hidden layer not only impacts the output but also gives feedback to itself. The structure of an RNN model is shown in Fig.  6 .

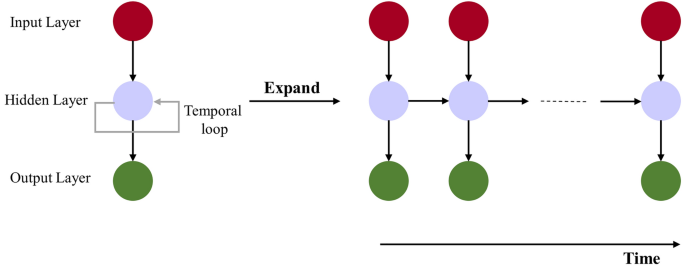
Structure of RNN model. Microsoft Visio 2019 was used to draw the visual concept of LSTM based on the Authors’ understanding of the model. https://www.microsoft.com/en-us/microsoft-365/visio/flowchart-software .

In sequence prediction problems, Long Short-Term Memory (LSTM) networks are a specific type of RNN that can learn the dependency in the sequence of time-series data. Since there could be a lag between the events of interest in a time series, these networks can perform well with different types of problem such as classification, processing, and prediction using time series data. One important issue in the standard RNN models is the inefficiency of the model to learn when there are time lags greater than five to ten discrete time steps between the input data target variable that can cause a vanishing gradient—that is, the gradient is too small, preventing the weight from changing its value. LSTMs were developed to cope with the problem of vanishing gradient. They can learn to connect minimal time lags when there exist many discrete time steps by enforcing constant error flow through special units, called cells; see Eqs. ( 2 ) and ( 3 ). In LSTMs, the flow of information is controlled through gates that keep or override information in the memory cell, forgetting previous information, and deciding how to access memory cell; see Eq. ( 4 ). An LSTM consists of three gates. The two gates that learn to open and close access to error within the memory cell are input and output gates. The third type of gate is the forget gate that has a specific role to reset operations for the cells. In another word, the input gate decides how much of the new state h [ t ] should be updated; the output gate determines the portion of the state that must be outputted; and the forget gate decides the part of the information that needs to be forgotten and eliminated from the previous cell state h [ t -1]. The main flow of information happens through a cell state. The cell state is updated in a forward process and the output is computed as displayed in Eq. ( 5 ):

where x [ t ] is the input at time t , σ (·) is a sigmoid function, g 1 (·) and g 2 (·) denote the point wise nonlinear activation function, (∙) denotes the entry wise multiplication between two vectors, R o , R u , R h , and R f represents weight matrices of the recurrent connections, W o , W u , W h , and W f are weight matrices for the inputs of LSTM cells, b o , b u , b f , and b h are bias vectors 5 . The LSTM model was developed in Python (v3.7.3) using the Keras (v2.2.4) Deep Learning Library that itself uses TensorFlow (v2.0.0b0) in the backend.

Model execution and validation

In this study, the dataset is split into two groups: the first 22 days of November for training and the last 8 days of November for testing. The groups were not split randomly on purpose to ensure both the training and testing sets had weekdays and weekends. Moreover, it is a common practice when modeling time series to use earlier data for training and later data for testing. The premise is that a good model should be able to capture new, unseen trends. We kept the same practice even our goal is not to develop the best performing model, but to study interrelationships.

Around 250 LSTM models were trained and compared to select optimal hyperparameters. The hyperparameters used in the end are as follows: number of epochs: 200; batch size: 50; learning rate: 0.001, optimizer: Adam; activation function: sigmoid; loss function: Binary crossentropy.

In terms of performance, we use goodness of fit \({R}^{2}\) , mean absolute error (MAE), and root mean squared error (RMSE) defined as:

where \({y}_{i}\) is the actual value of a data point, \({\widehat{y}}_{i}\) is the predicted value, \(n\) is the number of data points, and \(\overline{y }\) is the mean value of all \(n\) actual values.

To calculate the correlation between two time-series we use Pearson r value, defined as:

where \(x\) and \(y\) are the data points of two time-series and \({m}_{x}\) and \({m}_{y}\) are the mean of the vector \(x\) and \(y\) respectively.

Data availability

Traffic volume data is collected by the Gateway Traveler Information System and provided by the Illinois Department of Transportation (IDOT) to some of the team members. The authors were not granted the right to share the data. Electricity data was collected from Commonwealth Edison (ComEd). Anyone can access it for a fee at  https://www.comed.com/SmartEnergy/InnovationTechnology/pages/anonymousdataservice.aspx (accessed March 15, 2023).

Derrible, S. Urban engineering for sustainability (MIT Press, 2019).

Google Scholar  

Sarwat, A. I., Sundararajan, A., Parvez, I., Moghaddami, M. & Moghadasi, A. Toward a smart city of interdependent critical infrastructure networks. In Sustainable interdependent networks 21–45 (Springer, 2018).

Chapter   Google Scholar  

Movahedi, A, & Derrible, S. Interrelationships between electricity, gas, and water consumption in large‐scale buildings. J. Ind. Ecol. 1–16. https://doi.org/10.1111/jiec.13097 (2020).

Zhang, P. & Zhen (Sean) Qian.,. User-centric interdependent urban systems: using time-of-day electricity usage data to predict morning roadway congestion. Transport. Res. Part C Emerg. Technol. 92 (July), 392–411. https://doi.org/10.1016/j.trc.2018.05.008 (2018).

Article   Google Scholar  

Marvin, S. & Slater, S. The new urban infrastructure crisis competition for urban space. Public Works Manag. Policy 2 (2), 148–158 (1997).

Fan, Y., Lee, A., Parker, N., Scheitrum, D., Dominguez-Faus, R., Jaffe, A. M., & Medlock III, K. Geospatial, temporal and economic analysis of alternative fuel infrastructure: The case of freight and US natural gas markets. Energy J. 38 (6) (2017).

Hunt, S. D. A general theory of competition: Resources, competences, productivity, economic growth. Sage Publications (1999).

Ahmad, N. & Derrible, S. An information theory based robustness analysis of energy mix in US States. Energy Policy 120 , 167–174 (2018).

Bikcora, C., Verheijen, L. & Weiland, S. Density forecasting of daily electricity demand with ARMA-GARCH, CAViaR, and CARE econometric models. Sustain. Energy Grids Netw. 13 , 148–156 (2018).

Wu, F., Cattani, C., Song, W. & Zio, E. Fractional ARIMA with an improved cuckoo search optimization for the efficient Short-term power load forecasting. Alex. Eng. J. 59 (5), 3111–3118 (2020).

Torkzadeh R., Mirzaei, A., Mirjalili, M. M., Anaraki, A. S., Sehhati, M. R., & Behdad, F. Medium term load forecasting in distribution systems based on multilinear regression & principal component analysis: A novel approach. in Proc. 19th Conf. Elect. Power Distrib. Netw. (EPDC) , May 2014, pp. 66–70 (2014).

Wang, Z. X., Li, Q. & Pei, L. L. A seasonal GM (1, 1) model for forecasting the electricity consumption of the primary economic sectors. Energy 154 , 522–534 (2018).

Zheng, Z., Chen, H. & Luo, X. A Kalman filter-based bottom-up approach for household short-term load forecast. Appl. Energy 250 , 882–894 (2019).

Dong, Y., Ma, X. & Fu, T. Electrical load forecasting: A deep learning approach based on K-nearest neighbors. Appl. Soft Comput. 99 , 106900 (2021).

Esener, İI., Yüksel, T. & Kurban, M. Short-term load forecasting without meteorological data using AI-based structures. Turk. J. Electr. Eng. Comput. Sci. 23 (2), 370–380 (2015).

Zor, K., Timur, O., & Teke, A. A state-of-the-art review of artificial intelligence techniques for short-term electric load forecasting. In  2017 6th international youth conference on energy (IYCE)  (pp. 1–7). IEEE (2017).

Lee, D., Derrible, S. & Pereira, F. C. Comparison of four types of artificial neural network and a multinomial logit model for travel mode choice modeling. Transp. Res. Rec. 2672 (49), 101–112. https://doi.org/10.1177/0361198118796971 (2018).

Seyrfar, A., Ataei, H., Movahedi, A. & Derrible, S. Data-driven approach for evaluating the energy efficiency in multifamily residential buildings. Pract. Period. Struct. Des. Constr. 26 (2), 04020074. https://doi.org/10.1061/(ASCE)SC.1943-5576.0000555 (2021).

Kashani, H., Movahedi, A. & Morshedi, M. A. An agent-based simulation model to evaluate the response to seismic retrofit promotion policies. Int. J. Disaster Risk Reduct. 33 , 181–195. https://doi.org/10.1016/j.ijdrr.2018.10.004 (2019).

Liao, G. C. & Tsao, T. P. Application of a fuzzy neural network combined with a chaos genetic algorithm and simulated annealing to short-term load forecasting. IEEE Trans. Evol. Comput. 10 (3), 330–340 (2006).

Ling, S. H., Leung, F. H. F., Lam, H. K., Lee, Y. S. & Tam, P. K. S. A novel genetic-algorithm-based neural network for short-term load forecasting. IEEE Trans. Industr. Electron. 50 (4), 793–799 (2003).

Han, X. S., Han, L., Gooi, H. B. & Pan, Z. Y. Ultra-short-term multi-node load forecasting—a composite approach. IET Gener. Transm. Distrib. 6 (5), 436–444 (2012).

Parsa, A.B., Movahedi, A., Taghipour, H., Derrible, S., & Mohammadian, A. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis, Accid. Anal. Prev., 136 (2020). https://doi.org/10.1016/j.aap.2019.105405

Badhrudeen, M., Naranjo, N., Movahedi, A., & Derrible, S. Machine learning based tool for identifying errors in CAD to GIS converted data. In Proc., CIGOS 2019, Innovation for Sustainable Infrastructure, 1185–1190. Singapore: Springer (2020).

Lee, D., Mulrow, J., Haboucha, C. J., Derrible, S. & Shiftan, Y. Attitudes on autonomous vehicle adoption using interpretable gradient boosting machine. Transp. Res. Rec. 2673 (11), 865–878. https://doi.org/10.1177/0361198119857953 (2019).

Bouktif, S., Fiaz, A., Ouni, A. & Serhani, M. A. Optimal deep learning lstm model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches. Energies 11 (7), 1636 (2018).

Ren, Y., Suganthan, P. N., Srikanth, N. & Amaratunga, G. Random vector functional link network for short-term electricity load demand forecasting. Inf. Sci. 367 , 1078–1093 (2016).

Guo, Z., Zhou, K., Zhang, X. & Yang, S. A deep learning model for short-term power load and probability density forecasting. Energy 160 , 1186–1200 (2018).

Sarvestani, S. E. et al. Forecasting blood demand for different blood groups in Shiraz using auto regressive integrated moving average (ARIMA) and artificial neural network (ANN) and a hybrid approaches. Sci. Rep. 12 (1), 22031. https://doi.org/10.1038/s41598-022-26461-y (2022).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Ward, T. et al. Forecasting SARS-CoV-2 transmission and clinical risk at small spatial scales by the application of machine learning architectures to syndromic surveillance data. Nat. Mach. Intell. 4 , 814–827. https://doi.org/10.1038/s42256-022-00538-9 (2022).

Ma, R. et al. The prediction and analysis of COVID-19 epidemic trend by combining LSTM and Markov method. Sci. Rep. 11 , 17421. https://doi.org/10.1038/s41598-021-97037-5 (2021).

Benvenuto, D., Giovanetti, M., Vassallo, L., Angeletti, S., & Ciccozzi, M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief. 29 , 105340 (2020). https://doi.org/10.1016/j.dib.2020.105340 .

Abduljabbar, R. L., Dia, H. & Tsai, P. W. Development and evaluation of bidirectional LSTM freeway traffic forecasting models using simulation data. Sci. Rep. 11 , 23899. https://doi.org/10.1038/s41598-021-03282-z (2021).

Wang, W. et al. An interpretable model for short term traffic flow prediction. Math. Comput. Simul. 171 , 264–278 (2020).

Article   MathSciNet   MATH   Google Scholar  

Hor, C. L., Watson, S. J. & Majithia, S. Analyzing the impact of weather variables on monthly electricity demand. IEEE Trans. Power Syst. 20 (4), 2078–2085 (2005).

Article   ADS   Google Scholar  

Apadula, F., Bassini, A., Elli, A. & Scapin, S. Relationships between meteorological variables and monthly electricity demand. Appl. Energy 98 , 346–356 (2012).

Quan, S. J., Economou, A., Grasl, T. & Yang, P. P. J. An exploration of the relationship between density and building energy performance. Urban Des. Int. 25 (1), 92–112 (2020).

Barton, H. City of well-being: A radical guide to planning. Taylor & Francis (2016).

Proque, A. L., dos Santos, G. F., Junior, A. A. B., & Larson, W. D. Effects of land use and transportation policies on the spatial distribution of urban energy consumption in Brazil. Energy Econ. 104864 (2020).

Yang, P. P. Energy resilient urban form: A design perspective. Energy Proc. 75 , 2922–2927 (2015).

Stephan, A. & Crawford, R. H. The relationship between house size and life cycle energy demand: Implications for energy efficiency regulations for buildings. Energy 116 , 1158–1171. https://doi.org/10.1016/j.energy.2016.10.038 (2016).

Estiri, H. Household energy consumption and housing choice in the US residential sector. Hous. Policy Debate 26 (1), 231–250 (2016).

Filippín, C., Ricard, F. & Larsen, S. F. Evaluation of heating energy consumption patterns in the residential building sector using stepwise selection and multivariate analysis. Energy Build. 66 , 571–581 (2013).

Hunt, R., & Suhr, M. Old House Eco Handbook: A practical guide to retrofitting for energy efficiency and sustainability. White Lion Publishing. (2019).

Sanaieian, H., Tenpierik, M., Van Den Linden, K., Seraj, F. M. & Shemrani, S. M. M. Review of the impact of urban block form on thermal performance, solar access and ventilation. Renew. Sustain. Energy Rev. 38 , 551–560 (2014).

Ko, Y. Urban form and residential energy use: A review of design principles and empirical findings. J. Plan. Lit. 28 , 327–351. https://doi.org/10.1177/0885412213491499 (2013).

Article   CAS   Google Scholar  

Karatas, A., Stoiko, A. & Menassa, C. C. Framework for selecting occupancy-focused energy interventions in buildings. Build. Res. Inf. 44 (5–6), 535–551 (2016).

Broberg, T. & Egüez, A. Blame it on the owner—Ownership and energy performance of multi-dwelling buildings. Energy Econ. 72 , 108–119 (2018).

Li, C., Song, Y., Kaza N., & Burghardt R. Explaining spatial variations in residential energy usage intensity in Chicago: The Role of Urban Form and Geomorphometry. J. Plan. Educ. Res. 0739456X19873382 (2019).

Estiri, H. & Zagheni, E. Age matters: Ageing and household energy demand in the United States. Energy Res. Soc. Sci. 55 , 62–70 (2019).

Umit, R., Poortinga, W., Jokinen, P. & Pohjolainen, P. The role of income in energy efficiency and curtailment behaviours: Findings from 22 European countries. Energy Res. Soc. Sci. 53 , 206–214 (2019).

Derrible, S. An approach to designing sustainable urban infrastructure. MRS Energy Sustain. 5 , E15. https://doi.org/10.1557/mre.2018.14 (2018).

Cordova, J. et al. Combined electricity and traffic short-term load forecasting using bundled causality engine. IEEE Trans. Intell. Transp. Syst. 20 (9), 3448–3458 (2018).

Madhavi, K. L., Gilanifar, M., Zhou, Y., Ozguven, E. E., & Arghandeh, R. Multivariate deep causal network for time series forecasting in interdependent networks. In  2018 IEEE Conference on Decision and Control (CDC)  (pp. 6476–6481). IEEE (2018).

Gilanifar, M., Wang, H., Ozguven, E. E., Zhou, Y. & Arghandeh, R. Bayesian spatiotemporal gaussian process for short-term load forecasting using combined transportation and electricity data. ACM Trans. Cyber-Phys. Syst. 4 (1), 1–25 (2019).

Aparicio, J., Rosca, J., Mediger, M., Essl, A., Arzig, K., & Develder, C. Exploiting road traffic data for very short term load forecasting in smart grids. In ISGT 2014 (pp. 1–5). IEEE (2014).

ComEd, Anonymous Data Service Product Offering. (2021). https://www.comed.com/SmartEnergy/InnovationTechnology/pages/anonymousdataservice.aspx . Accessed 05 Oct 2021.

Wong, J., & Rajagopal, R. A simple way to use interval data to segment residential customers for energy efficiency and demand response program targeting. In ACEEE Proceedings (2012).

Parker, S. A., Hunt, W. D., McMordie Stoughton, K., Boyd, B. K., Fowler, K. M., Koehler, T. M., & Pugh, R. Metering best practices: A guide to achieving utility resource efficiency, release 3.0 (No. PNNL-23892-Rel. 3.0). Pacific Northwest National Lab.( PNNL), Richland, WA (United States) (2015).

Fumo, N. & Biswas, M. R. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 47 , 332–343 (2015).

Mashima, D., & Roy, A. Privacy preserving disclosure of authenticated energy usage data. In  2014 IEEE international conference on smart grid communications (SmartGridComm) (pp. 866–871). IEEE (2014).

Martínez, S., Sebé, F., & Sorge, C. Measuring privacy in smart metering anonymized data (2020). arXiv preprint arXiv:2002.04863 .

Dietrich, A., Leibenger, D., & Sorge, C. On the Lack of Anonymity of Anonymized Smart Meter Data: An Empiric Study. In  2020 IEEE 45th Conference on Local Computer Networks (LCN)  (pp. 405–408). IEEE (2020).

Rice, K., Higgins, J. P. T. & Lumley, T. A re-evaluation of fixed effect(s) meta-analysis. J. R. Stat. Soc. A. Stat. Soc. 181 (1), 205–227. https://doi.org/10.1111/rssa.12275 (2018).

Helmrich, A. et al. Centralization and decentralization for resilient infrastructure and complexity. Environ. Res. Infrastruct. Sustain. 1 (2), 021001 (2021).

Download references

Acknowledgements

This research was partly supported by the National Science Foundation (NSF) CAREER award #1551731.

Author information

Authors and affiliations.

Department of Civil, Materials, and Environmental Engineering, University of Illinois at Chicago, 842 W Taylor Street (M/C 246), Chicago, IL, 60607, USA

Ali Movahedi, Amir Bahador Parsa, Abolfazl Kouros Mohammadian & Sybil Derrible

Department of Urban Planning and Policy, University of Illinois at Chicago, 412 S Peoria St, Chicago, IL, 60607, USA

Anton Rozhkov

Department of Policy and Administration, Incheon National University, Incheon, 22012, South Korea

Dongwoo Lee

Institute for Environmental Science and Policy, University of Illinois at Chicago, 1603 West Taylor Street, Chicago, IL, 60607, USA

• Sybil Derrible

You can also search for this author in PubMed   Google Scholar

Contributions

A.M.: conceptualization, methodology, data curation, formal analysis, writing original—draft, software, submission. A.B.P: methodology, data curation, software. A.R: Writing original—draft, software. D.L: writing, reviewing, and editing. A.K.M.: data curation, writing, reviewing, and editing. S.D.: conceptualization, formal analysis, writing, reviewing, and editing, funding acquisition.

Corresponding author

Correspondence to Ali Movahedi .

Ethics declarations

Competing interests.

The authors declare no competing interests, but one of the coauthors, Prof. Sybil Derrible, is a member of the editorial board of Scientific Reports.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Movahedi, A., Parsa, A.B., Rozhkov, A. et al. Interrelationships between urban travel demand and electricity consumption: a deep learning approach. Sci Rep 13 , 6223 (2023). https://doi.org/10.1038/s41598-023-33133-y

Download citation

Received : 11 January 2023

Accepted : 07 April 2023

Published : 17 April 2023

DOI : https://doi.org/10.1038/s41598-023-33133-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Advanced transport systems: the future is sustainable and technology-enabled.

Scientific Reports (2024)

Depopulation and associated challenges for US cities by 2100

• Uttara Sutradhar
• Lauryn Spearing

Nature Cities (2024)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

The measurement of urban travel demand

1974, Journal of Public Economics

Related Papers

Working Papers

Elisabetta Venezia

This paper presents some empirical results stemming from the estimation of a random utility model. With regard to the case study, the main findings are that notwithstanding the existence of a mediocre transport urban service, people would be in favour of using buses ...

PROCEEDINGS OF THE AET EUROPEAN TRANSPORT CONFERENCE, HELD 10-12 SEPTEMBER, 2001, HOMERTON COLLEGE, CAMBRIDGE, UK - CD-ROM

Pierluigi Coppola

ALI ALSHAHIBI

Transportation Research Record: Journal of the Transportation Research Board

Kay Axhausen

Johan Holmgren

Socio-Economic Planning Sciences

Kenneth Button

A Companion to Urban Economics

Nathalie Picard

Zenodo (CERN European Organization for Nuclear Research)

Muhammad Zaly Shah

RELATED PAPERS

Asian Journal of Finance & Accounting

Ameen Talib

Journal of Environmental Geography

Diaa Sheishah

SUNGKOWO SOETOPO

Clinical Nutrition

SIMONE BRASIL DE OLIVEIRA IGLESIAS

DAYAH: Journal of Islamic Education

Teuku Zulkhairi

hukyytj jkthjfgr

British Journal of Cancer

Börje Ljungberg

JAAD Case Reports

Cristian Gonzalez

International Journal of Advanced Computer Science and Applications

HAL (Le Centre pour la Communication Scientifique Directe)

Martin Laliberté

Journal of Range Management

Ned Fetcher

Revista Anagramas

Rejane Markman

Armin Doerry

Theoretical and Applied Economics

Carmen Obreja

Subtropical and ornamental horticulture

Michael Blanke

DergiPark (Istanbul University)

husniye calisir

CABI eBooks

Alice Murage

Ponto E Virgula Revista De Ciencias Sociais Issn 1982 4807

Noêmia Lazzareschi

Julio Perez Carreon

Jean-Marc Tacnet

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

Impact of the mixed degree of urban functions on the taxi travel demand

Roles Conceptualization, Methodology, Writing – original draft, Writing – review & editing

Affiliations College of Transportation Engineering, Chang’an University, Xi’an, China, Engineering Research Center of Highway Infrastructure Digitalization, Ministry of Education, Xi’an, China, Xi’an Key Laboratory of Digitalization of Transportation Infrastructure Construction and Management, Xi’an, China

Roles Conceptualization, Data curation, Methodology, Visualization, Writing – original draft, Writing – review & editing

* E-mail: [email protected]

Affiliation College of Transportation Engineering, Chang’an University, Xi’an, China

Roles Writing – original draft, Writing – review & editing

Affiliations College of Transportation Engineering, Chang’an University, Xi’an, China, Engineering Research Center of Highway Infrastructure Digitalization, Ministry of Education, Xi’an, China, Xi’an Key Laboratory of Digitalization of Transportation Infrastructure Construction and Management, Xi’an, China, Department of Civil and Environmental Engineering, University of Waterloo, Waterloo, Canada

Roles Data curation, Writing – original draft

Roles Data curation, Writing – review & editing

• Changwei Yuan, 
• Yaxin Duan, 
• Xinhua Mao, 
• Ningyuan Ma, 
• Jiannan Zhao

• Published: March 4, 2021
• https://doi.org/10.1371/journal.pone.0247431
• Reader Comments

As an important service industry in cities, taxis provide people with an all-weather travel mode. And its demand is greatly affected by the internal functions of the city. It is very important to understand the relationship between the mixed degree of urban internal functions and the residents’ taxi travel demand to alleviate traffic congestion and formulate corresponding urban traffic strategies. This paper combined two heterogeneous data in the main urban area of Xi’an, urban points of interest (POIs) and taxi GPS. Firstly, a spatial information entropy model was constructed to quantitatively evaluate the mixed degree of functions in different spaces within the city. Secondly, the kernel density estimation method was used to analyze the spatial distribution evolution characteristics of residents’ taxi travel demand. A geographically weighted regression (GWR) model was further used to study the spatial and temporal influences of the mixed degree of urban internal functions on taxi travel demand. Results indicate that there is an obvious spatiotemporal pattern in the impact of the mixed degree of urban functions on taxi travel demand. And the GWR model is used to study the impact is superior to the ordinary least squares (OLS). In more developed areas, improving the mixed degree of urban functions will be more attractive than backward areas. It is also found that although the single function of the city has an impact on the taxi travel demand, the result of the single function is not ideal. This study can provide a reference for the optimal combination of basic units of urban space in urban planning, promote the balance of supply and demand of urban taxis, rationalize urban taxis’ operation and allocation, and solve the problems of urban transportation systems.

Citation: Yuan C, Duan Y, Mao X, Ma N, Zhao J (2021) Impact of the mixed degree of urban functions on the taxi travel demand. PLoS ONE 16(3): e0247431. https://doi.org/10.1371/journal.pone.0247431

Editor: Bing Xue, Institute for Advanced Sustainability Studies, GERMANY

Received: October 14, 2020; Accepted: February 7, 2021; Published: March 4, 2021

Copyright: © 2021 Yuan et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: All relevant data are within the manuscript and its Supporting Information files.

Funding: This research was funded by the Ministry of Education of Humanities and Social Science Project (grant number 18YJAZH120); The Key Research Base project of Philosophy and Social Science of Education Department of Shaanxi Province (grant number 19JZ008).

Competing interests: The authors have declared that no competing interests exist.

1. Introduction

Taxis, as an important part of urban transport with flexible and convenient conditions, provide all-weather travel services, and play an indispensable role in urban resident trips [ 1 , 2 ]. In recent years, with the expansion of the urban population and diversification of social activities, people’s demand for taxi travel has increased dramatically. In addition, with the gradual standardization of online taxi booking, taxi passenger volume has grown substantially. According to the 2018 Xi’an transport development annual report, there were 12,535 taxis in the city, carrying 361 million passengers in 2018, and an average of 990,000 passengers per day in 2018 [ 3 ]. However, due to the imbalance of the spatial distribution of pedestrian flow and the uncertainty of travel time, the taxi travel demand has a complex space-time dependence. Additionally, if taxi drivers do not have full knowledge of high-demand areas, it will inevitably lead to a significant imbalance between supply and demand in the taxi industry, traffic congestion, long waiting times of passengers, and other such phenomena. Therefore, it is necessary to dig deep into the residents’ taxi travel demand.

However, exploring the taxi travel demand has always been the focus of academic circles. Firstly, considering that residents’ taxi travel demand has obvious temporal and spatial distribution characteristics, how to use taxi GPS data to clarify these temporal and spatial distribution characteristics is an important basis. Secondly, the purpose of residents’ taxi travel is diverse, which is largely affected by the interaction of urban internal functions. In order to measure the interaction of this kind of urban internal functions, we introduce the concept of the mixed degree of urban functions. It is composed of urban points of interest (POIs), the basic units of urban space. And in recent years, web crawler technology has been widely used in various fields [ 4 – 6 ], providing important technical support for obtaining the data related to these urban POIs. These open urban POIs data can be used as the important data source for studying the urban internal functions [ 7 , 8 ]. Then, how to use the urban POI data to quantitatively evaluate the mixed degree of urban functions and study its impact on the temporal and spatial dynamic changes of taxi travel demand is still lacking.

Therefore, this paper uses urban POI data and taxi GPS data to explore the relationship between the mixed degree of urban functions and residents’ taxi travel demand. Based on GIS technology, a spatial information entropy model is constructed to measure the mixed degree of urban functions and realize the spatialization of the information entropy model. The paper also uses Python big data analysis technology and kernel density estimation method to analyze the spatial distribution and evolution characteristics of taxi travel demand. Finally, the geographically weighted regression (GWR) model is used to verify the spatial-temporal differentiation pattern of residents’ taxi travel behavior and the mixed degree of urban functions. This study can offer a reference for the optimal combination of basic units of urban space in urban planning. Our work also provides a decision-making basis for promoting the balance of urban taxi supply and demand, solving the development of the urban taxi industry, and alleviating the urban traffic system problems in the formulation of traffic strategy.

The remainder of this paper is as follows. Section 2 summarizes the spatial-temporal variation characteristics of residents’ taxi travel, the influencing factors, and research methods. Section 3 outlines the research methods used in this article, including the spatial information entropy for the mixed degree of urban functions measurement, the kernel density estimation for taxi travel demand measurement, and the GWR model. Section 4 introduces the study area and data, including urban POI data and taxi GPS track data. Section 5 provides the model result and discussion. Section 6 summarizes the conclusions. Section 7 provides the limitations and future work.

2. Literature review

In recent years, with the popularization of mobile application technology and taxi GPS devices, a large amount of data related to individuals’ positions and trajectories has spring up [ 9 ]. All these provide an important scientific basis for the refined study of the spatial and temporal distribution characteristics of residents’ taxi travel. For example, in order to explore the mode of travel demand in New York City and improve the efficiency of taxi companies, Tang et al. [ 10 ] analyzed the spatial and temporal distribution characteristics of travel demand in different regions by extracting the location data of passenger points from the GPS track data of New York City taxis. Based on the hidden Markov model, Alvarez-Garcia et al. [ 11 ] analyzed the temporal and spatial characteristics of taxi driving using past GPS logs and current location. Bischoff et al. [ 12 ] analyzed the travel behavior and vehicle supply of the Berlin taxi market based on the GPS data of taxis. And the time analysis showed that there would be peak demand in the morning and afternoon of weekdays, and the peak demand would turn to night on weekends. The spatial analysis showed that most taxi travels involved city centers and airports. All of these studies conducted beneficial exploration of the spatiotemporal variation rules and behavior patterns of residents’ taxi travels.

On this basis, many scholars further discussed the influencing factors of the spatial and temporal distribution characteristics, which were mainly divided into three categories. The first category is the urban built environment factors. For example, Zhang et al. [ 13 ] took urban built environment, road length, road density, residential building quantity, residential building density, employment place, and public service as important factors to analyze the temporal and spatial impact of taxi traffic by using the geographically and temporally weighted regression (GTWR) model. Wu et al. [ 14 ] studied the spatial distribution characteristics of taxi routes in downtown Shanghai and established a multiple linear regression model to quantitatively analyze the impact of the urban construction environment on short-distance taxi trips in the city. The second category is the weather factors. For example, Kamga et al. [ 15 ] analyzed the impact of weather changes on the balance of supply and demand of taxis based on a 10-month GPS data set of a taxi in New York City, and found that rainy weather often leads to higher passenger capacity. Based on the data of taxis, meteorology, and air quality, Kang et al. [ 16 ] conducted a spatial-temporal analysis of residents’ taxi travel demand and loading and unloading areas in different weather and revealed the relationship between the weather and the taxi travel activities of residents. The third category is the land-use factors. Jiang et al. [ 17 ] established a linear relationship between taxi travel behavior and land-use using taxi track data and POI data of urban interest points. Liu et al. [ 18 ] used taxi track data to study the variation of passenger volume over time and the relationship between this and different land-use characteristics. The research results are helpful for urban planners and decision-makers to alleviate the issues of transportation and resources.

In the analysis of the influencing factors of residents’ taxi travel demand, the most traditional methods are the ordinary least squares (OLS) multiple regression model [ 19 – 21 ] and the four-stage method [ 22 ]. An important assumption of the ordinary least squares multiple regression model is that all variables in the study area are stable and independent, and the variance of the error term is the same [ 23 ]. The method is characterized by fast and convenient calculation, which is more suitable for analyzing the travel demand of specific travel modes. However, due to the different purposes of residents’ taxi travel and the spatial differences of urban internal functions, local spatial changes will not be captured and the accuracy of model results will be reduced if such spatial differences are ignored. In order to overcome this defect, some scholars have utilized the GWR model. Since the GWR model explains the spatial distribution differences of the research objects well [ 24 – 26 ], it has been widely used in the analysis of spatial heterogeneity [ 27 – 30 ].

To sum up, the aforementioned studies mainly used GPS track data of taxis to analyze the spatial and temporal distribution characteristics of residents’ taxi travel and the influencing factors of such characteristics. These studies set each factor as a single variable, where influencing factors’ combined effects are not comprehensively considered. However, the taxi travel demand of urban residents, that is, the purpose of travel, is largely affected by the interaction of urban internal functions. Due to their continuous development, it is hard to divide a city into a set of single functional areas, which can easily cause the disconnection of various elements of urban ecology. We should recognize the connection and importance of multi-functional living environments and social interaction spaces [ 31 ]. In this situation, function mixing has appeared in cities. Urban function mixing is to compact arrange a series of interrelated functions in the same area, so as to reduce the travel cost and effectively improve the efficiency and public welfare level of the city [ 32 ]. Therefore, how to measure the mixed degree of urban functions and its influence on residents’ taxi travel demand is a problem worth discussing.

By presenting the concept of the urban function mixing, we use the ArcGIS and Python software to build a spatial information entropy model to measure the mixed degree of urban functions. We further use the kernel density estimation method to analyze the spatial distribution and evolution characteristics of taxi travel demand during the three peak periods of the morning, afternoon and evening on weekdays and weekends. Then, through the GWR Model, the spatial and temporal differences of the impact of the mixed degree of urban functions on taxi travel demand are further discussed by using regression coefficient. Finally, the influences of single function and mixed functions on taxi travel demand are compared. The overall research framework of the paper is shown in Fig 1 .

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

https://doi.org/10.1371/journal.pone.0247431.g001

3.1 Spatial information entropy for the mixed degree of urban functions measurement

Since a city contains a significant amount of information, it can be regarded as a spatial system where the urban POIs are denoted as various functional attributes. Then, we introduce the concept of information entropy at the spatial level, construct the spatial information entropy model, and use the information entropy to measure the mixed degree of different spatial functions in the city. The steps are as follows.

Step 1: The urban space is gridded by ArcGIS software. A rectangle that can cover the entire urbanized area is designed and then divided into m × n non-intersecting squares of equal size of a m × a m (as shown in Fig 2 , the blue part is assumed to be the urbanized area to be studied). The analysis unit does not adopt the traditional traffic analysis area, such as administrative division [ 35 ], block [ 36 ], or community [ 37 ], for three main reasons. The first reason is that the traditional traffic area is too large and the scale unit is not sufficiently fine. The second reason is that a grid allows the use of units that can be controlled, thus providing a reasonable scale to describe and understand the spatial distribution of the research objects. The third reason is that the grid processing is convenient for computing and allows the processing of a large amount of spatial data quickly.

https://doi.org/10.1371/journal.pone.0247431.g002

Step 3: Calculation of the mixed degree of urban functions. Through ArcGIS software, we can traverse the number of different types of POI data in each grid cell to obtain the values of each p ij and each H s . Namely, the functional mixing degrees of cities in different spaces have been obtained.

3.2 Kernel density estimation for taxi travel demand measurement

3.2.1 taxi travel demand measurement method..

Fig 3 presents the flow chart of the measurement method of taxi travel demand in this paper. First of all, it is necessary to transform and preprocess the acquired GPS track data file. Format conversion is used to convert the acquired original data file type into a file type that can be used to carry out data analysis. Preprocessing includes correction and elimination of duplicates, invalid data, data outside the research scope, and incomplete information.

https://doi.org/10.1371/journal.pone.0247431.g003

Then, we extract the OD (Here, point O, where the vehicle operation status changes from "empty vehicle" to "full vehicle". Point D, where the vehicle operation status changes from "full vehicle" to "empty vehicle".) points of the cleaned taxi data. Here, we only extract the data relating to the destination (point D), to represent a residents’ travel purpose and hence taxi demand.

Finally, coordinate transformation and map matching are carried out, and the number of points D in each grid cell that meshes the urban space is counted respectively.

3.2.2 Kernel density estimation method.

In order to reflect the spatial distribution and evolution characteristics of residents’ taxi travel demand more directly, this paper adopts the kernel density estimation method to analyze the variation of taxi travel demand density. The kernel density estimation method can be used to mine spatial data. It cannot only select the appropriate bandwidth flexibly according to the research scale but also has certain advantages in the aspect of detailed local characteristics. Using the first law of geography, this method holds that the closer the distance between things, the greater the density expansion value obtained from the proximity to the core elements, thus fully reflecting the spatial distribution position difference of the research object [ 38 ]. Accordingly, the kernel density estimation method is used to characterize the spatial distribution characteristics and rules of taxi boarding and alighting points. The spatial kernel density estimation is provided in Fig 4 .

https://doi.org/10.1371/journal.pone.0247431.g004

3.3 Geographically Weighted Regression (GWR) model

4. Study area and data

4.1 study area.

Xi’an is an important central city in the western region of China. By the end of 2018, Xi’an had a total area of 10,096.81 square kilometers, a permanent resident population of 10.037 million, and a well-developed transportation network. According to the 2018 traffic analysis reports for major cities in China, Xi’an had the highest proportion of public trips in the country in 2018 [ 39 ]. As an important part of public transport travel in Xi’an, the main urban area of Xi’an has a relatively large demand for taxi travel, representing 90% of the demand for taxi travel in the wider city. Therefore, this study took the main urban area of Xi’an as the study area, including the districts of Weiyang, Lianhu, Xincheng, Beilin, Yanta, and Baqiao ( Fig 5A ). In order to study the influence of the mixed degree of urban internal functions on taxi travel demand, after many attempts, the main urban area of Xi’an was divided into a grid of 500 × 500 m squares as the analysis unit. One is that it is more accurate in spatial structure study. Secondly, when a city is taken as the research area to study the taxi travel demand problem, it is usually divided into 500 m×500 m square grids [ 13 , 29 , 40 ]. The total number of analysis units was 3486 ( Fig 5B ), which is similar to the scale of the street units used in planning research.

(a) Administrative divisions in the study area; (b) grid generation of the study area.

https://doi.org/10.1371/journal.pone.0247431.g005

4.2 Data sources

The data sources used in this paper include the urban POI data collected from the Gaode Map and the GPS track data of taxis obtained from the taxi management office of Xi’an city.

4.2.1 Urban POI data.

The urban POIs describes the spatial and attribute information of geographical entities [ 41 ]. It is a basic unit that reflects various functions within a city, the spatial distribution of urban functions, and residents’ travel purposes [ 42 , 43 ]. The urban POI data used in this paper were from the Xi’an Gaode Map of 2019, and the POI data was collected using the Gaode Map. After coordinate transformation and address matching of the original data, a total of 308,450 POIs were obtained in the main urban area of Xi’an city. Each POI data point was captured with ten attributes: id, name, telephone, address, longitude coordinates, latitude coordinates, type, province, city and district. Here we only show 10 sets of data ( Table 1 ). And telephone numbers are no longer displayed because of privacy issues.

https://doi.org/10.1371/journal.pone.0247431.t001

According to the basic attributes of POI data, urban functional areas were divided into 13 categories: cater POI, tourist attraction POI, public facility POI, shopping POI, traffic facility POI, educational training POI, financial and insurance POI, commercial Residence POI, life service POI, sports leisure service POI, medical treatment POI, government agency POI, accommodation services POI ( Table 2 and Fig 6 ).

https://doi.org/10.1371/journal.pone.0247431.g006

https://doi.org/10.1371/journal.pone.0247431.t002

4.2.2 Taxi track data.

Taxi track data can reflect urban traffic operation, residents’ activity rules, and urban functional spatial structure. Except for special events, the number of trips per week is stable, and there is a repeated pattern every week [ 27 ]. Therefore, this paper used more than 2.7 million taxi track data from September 4th to September 10th, 2019 in Xi’an city for analysis. No major holidays occurred during the analyzed period, thereby eliminating the impact of contingencies, single day analysis errors, and thus allowing a complete appreciation of the characteristics of residents’ taxi travel demand. The obtained driving track data of each taxi included vehicle ID, time, direction, longitude and latitude, effectiveness, state, and other information. The specific data format is presented in Table 3 .

https://doi.org/10.1371/journal.pone.0247431.t003

Since the selected study area was the main urban area of Xi’an, it was necessary to extract and preprocess the obtained taxi track data of Xi’an to ensure consistency between the study area and the data coverage. The specific steps were as follows:

• Eliminating duplicate, invalid and data outside the main urban area of Xi’an city.
• Removing the data of travel time t < 2 min or t > 220 min.
• Extracting the data of point D from the OD point, that is, the point at which the vehicle operation state changes from a full vehicle to an empty vehicle (i.e., from state 5 to state 4).

After the above steps, a total of 2.4 million effective taxi tracks were obtained within the main urban area of Xi’an for one week.

5. Results and discussion

5.1 measurement results of the mixed degree of urban functions.

In order to show the spatial distribution of POIs in Xi’an more clearly, GIS software was used to visualize the POI data divided into 13 categories ( Fig 7 ).

https://doi.org/10.1371/journal.pone.0247431.g007

Furthermore, according to the spatial information entropy model proposed above and the measurement method of the mixed degree of functions in different spaces within the city, this paper used the regional statistical tool in the ArcGIS toolbox to calculate the spatial distribution of the 13 categories of POI data, and obtained the mixed degree of urban functions in each grid cell ( Fig 8 ). It can be seen that within the main urban area of Xi’an there is a certain spatial difference in the mixed degree of urban functions. And the multicenter characteristics are obvious. Overall, the mixed degree is lowest outside the third ring road and gives a trend of gradual increase within the third ring road. In particular, the mixed degree of urban POIs in some places outside the third ring road is as low as 0, but within the third ring road, the maximum is 1.0168.

https://doi.org/10.1371/journal.pone.0247431.g008

Among the areas of focus, the traditional Bell Tower business circle in Beilin district, Xiaozhai business circle in Yanta district, Exhibition Center, and High-Tech Road have the highest mixed degree, up to 0.8028–1.0618. This is because these areas have a large number of shopping malls, entertainment facilities, office buildings, restaurants, etc., showing diversity. These regions also have a relatively high proportion of taxi demand. One possible explanation is that more mixed areas are more attractive than others. The mixed degree of urban POIs is the second-highest in the area around the newly rising North City business circle in Weiyang district. These also reach more than 0.6539. In addition, the mixed degree of urban POIs near Xi’an High-Speed Railway station is also relatively low, mostly below 0.6538.

5.2 Measurement results of the taxi travel demand

5.2.1 results of the temporal distribution of taxi travel demand..

Taxi operation is flexible, and is not only influenced by the arrangement of taxi dispatching companies, but also by the subjective judgment of taxi drivers. We used the extracted and preprocessed taxi track data in the main urban area of Xi’an from September 4th to September 10th, 2019, to calculate the average hourly taxi demand in the same time period from Monday to Sunday, record the change of taxi travel demand in one day. And averaged it according to a single working day and a single rest day to get the average hourly taxi demand on weekdays and weekends ( Fig 9 ).

(a) Taxi demand average hourly from Monday to Friday; (b) taxi demand average hourly from Saturday to Sunday; (c) taxi demand per hour and per day.

https://doi.org/10.1371/journal.pone.0247431.g009

It can be seen from Fig 9 that the distribution of taxi travel demand at each time of the week was consistent with the travel rules of residents. There were three obvious peak periods: 8:30–10:30, 12:30–14:30, and 21:30–23:30. And the taxi travel demand was relatively high in the evening, and reached its maximum at about 22.30.

On weekdays, since the data extracted in this paper related to taxi drop-off points, there was a certain lag in time. Thus, the two peak periods, from 8:30 to 10:30 and from 12:30 to 14:30, corresponded to the commuting time of residents on weekdays. However, in the evening, some residents change from commuters to recreational travelers, and some buses in Xi’an stop operating after 19:30 or 20:30. Thus, a considerable portion of urban traffic demand is forced to turn to taxis and other means of transportation, increasing the number of residents’ taxi trips. As a result, the late peak period is pushed back from 17:30–19:30 to 21:30–23:30.

Compared with weekdays, during the periods of 0:00–6:00, 12:00–14:00 and 17:30–24:00 on weekends, the taxi travel demand was higher than that of working days, while other periods were lower than working days. This result is in line with residents’ daily travel habits. One reason is that most residents choose to rest on weekend mornings, they postpone their time to go out. Second, many residents choose to have leisure and entertainment activities on weekends, which always last until late at night. At this time, due to the suspension of buses, the probability of choosing to take a taxi to return to the residence increases, leading to an increase in the taxi travel demand. In general, taxi drivers can generate considerable income by attracting passengers after 21:00.

5.2.2 Results of the spatial distribution of taxi travel demand

In order to further study the agglomeration of taxi travel demand and its changes during different periods, this paper calculated the average hourly taxi demand of all grid cells in the same time period from Monday to Sunday. The calculation was based on the three time periods (8:30–10:30, 12:30–14:30, and 21:30–23:30) from Fig 9 to represent the morning, noon, and evening peaks of traffic in the main urban area of Xi’an respectively. The kernel density estimation method was used to analyze the time-space distribution and evolution characteristics of taxi travel demand during the three peak periods (Figs 10 and 11 ). It was found that different time spans presented obviously different travel patterns.

(a) Morning peak; (b) noon peak; (c) evening peak; (d) overall peak.

https://doi.org/10.1371/journal.pone.0247431.g010

https://doi.org/10.1371/journal.pone.0247431.g011

Figs 10D and 11D reveal the hot spot distribution of taxi travel demand in the main urban area of Xi’an for a whole day on weekdays and a whole day on weekends. It is found that the hot spots are similar, and they are mainly concentrated around the commercial centers of Yanta, Beilin, Xincheng, and Weiyang districts, as well as the High-Tech district with the good investment environment and active economic development. There are various types of functional facilities, such as catering, shopping, leisure and entertainment, life services, and offices. In addition, there are also hot spots around High-Speed and conventional Railway stations. This may be because the stations are surrounded by a large number of hotels, catering services, parking areas, etc. Outside of these areas, the taxi travel demand in other places is relatively weak. This indicates the spatial distribution of hot spots is related to the mixed degree of urban functions. That is to say, the taxi travel demand is affected by the mixed degree of urban functions, and the influence may be different in different spaces.

For the three peak periods on weekdays ( Fig 10A–10C ), it is found that the spatial distribution of the hot spots of residents’ taxi travel demand is constantly evolving and variable. Under the influence of the urban internal functions, Fig 10A represents that the hot spots are spread around the the Bell Tower, Xiaozhai, the High-Tech Industrial Park, the vertical section from Fengcheng No.1 Road to the City Sports Park, the High-Speed Railway Station, and the Xi’an Railway Station in the morning peak period. Fig 10B displays the noon peak period. The distribution of hot spots in the vertical section from Fengcheng No.1 Road to the City Sports Park has been reduced. This may be relevant to the midday rest system implemented by most enterprises. However, the distribution of hot spots near the Bell Tower, Xiaozhai, the Xi’an Railway Station, and the Exhibition Center has increased. Fig 10C represents that hot spots are more concentrated in the vicinity of the Bell Tower, the Electronics City, and the Exhibition Center during the evening peak period. Nevertheless, the taxi travel demand in the vertical section from Fengcheng No.1 Road to the City Sports Park is greatly reduced.

For the three peak periods on weekends ( Fig 11A–11C ), it is found that the hot spots are greatly reduced near the High-Tech Industrial Park in the morning peak period ( Fig 11A ). It may be that the High-Tech Industrial Park is the place for a large number of talents to work here, so the weekend off has caused a decrease in taxi travel. Fig 11B displays the noon peak period. The distribution of hot spots in the Bell Tower, Xiaozhai, and the Exhibition Center has been increased. This is connected to their irreplaceable geographical location, commercial status, etc. In Fig 11C during the evening peak period, multiple hotspots are formed. And the concentration range of the hot spots in the Bell Tower is greatly increased. This may be because residents often choose to go out for entertainment and shopping on weekend nights. However, the distribution of hot spots in the vertical section from Fengcheng No.1 Road to the City Sports Park is greatly reduced. On the one hand, this is related to the fact that it is the only route for residents in the northern suburbs to travel and the important transfer locations. On the other hand, it is related to the fact that some buses stop running after 19:30 and that consumers want to relax at night and are willing to pay higher transportation costs in exchange for more comfortable transportation services. They often choose to take a taxi directly from the starting point to the destination instead of taking a taxi to these exchange points for transfer.

To summarize, the above analysis indicates the influence of the mixed degree of urban functions on residents’ taxi travel demand in a city is not only different spatially, but also temporally. Thus, it is important to further clarify these differences.

5.3 Measurement results of geographically weighted regression

We further study the spatial differences of the influence of the mixed degree of urban functions on residents’ taxi travel demand, and the evolution in different peak traffic periods. This paper took each grid cell in the research area as the research unit, the taxi travel demand of residents in each grid cell as the dependent variable, and the mixed degree of urban internal functions in each grid cell as the explanatory variable to construct the global OLS and the GWR models on weekdays and weekends. The comparison results are as follows (Tables 4 and 5 ).

https://doi.org/10.1371/journal.pone.0247431.t004

https://doi.org/10.1371/journal.pone.0247431.t005

It can be seen from Tables 4 and 5 that the adjusted R 2 values of the GWR model are higher than those of the global OLS model whether on weekdays or weekends. These results all indicate that the GWR model considering temporal and spatial effects can improve the goodness of fit of the model obviously. Moreover, on weekdays, the AIC C values of the GWR model are lower than those of the OLS model; the difference values are greater than 3. So it is also considered that the model with the lower AIC C is better [ 44 ]. The results obtained at the weekend are the same. This again reveals that the GWR model is better than the OLS model in studying the impact of the mixed degree of urban functions on residents’ taxi travel demand. Further analysis of results is as follows.

Figs 12 and 13 give the spatial distribution results of the H s coefficient of the mixed degree of urban functions in the three peak periods and the whole day on weekdays and weekends, using the GWR Model. Generally, the impact of the mixed degree of urban functions on the residents’ taxi travel demand shows temporal and spatial differences.

https://doi.org/10.1371/journal.pone.0247431.g012

(a) Morning peak; (b) noon peak; (c) evening peak; (d) whole day.

https://doi.org/10.1371/journal.pone.0247431.g013

From the perspective of spatial differences, whether on weekdays or weekends, compared with the north–south direction, the east–west direction has a greater difference in the impact of the mixed degree of urban functions on residents’ taxi travel demand. And in these two directions, the differences in the H s coefficient on weekdays are greater than those on weekends. In addition, the regression coefficient values in the north-south direction are basically positive proportional, excluding the area near the High-Speed Rail Station and Xiaozhai. And the impact during the weekdays is greater than the weekends. Near the Electronics City, Xiaozhai, the Exhibition Center, and the High-Tech Industrial Park, the mixed degree of urban function has the greatest impact on residents’ taxi travel demand, and they are all in positive proportional. It shows that the higher the mixed degree of urban functions, the greater the taxi travel demand [ 45 ]. To a certain extent, this confirms that regions with high POI diversity are more attractive than other regions, which is consistent with Crane et al. [ 46 ], who believes that improving the accessibility of multiple destinations can increase travel demands. In particular, in the north-east, south-east and north-west corner of the main urban area, the mixed degree of urban functions has the little impact on the residents’ taxi travel demand, with most areas showing an inverse proportion.

From the perspective of temporal differences, the Bell tower, the Exhibition Center, the High-Tech Industrial Park, and the Xi’an Railway Station, as an important commercial center, high-tech area, and transportation hub, are irreplaceable in the city. They attract residents from other regions all day long. Therefore, in the three peak periods and the whole day on weekdays and weekends, the demand for taxi travel shows an increasing trend with the increase of the mixed degree of urban functions. However, compared with the morning and noon peak periods, the mixed degree of urban functions has less influence on the residents’ taxi travel demand in the evening peak period from the vertical section from Fengcheng No.1 Road to the City Sports Park. And the impact is less on weekdays than on weekends. In addition, whether on weekdays or weekends, near the High-Tech Industrial Park, the taxi travel demand decreases with the increase of the mixed degree of urban functions during the morning and noon peaks compared with the evening peak period. This may be caused by that the High-Tech Industrial Park is mainly based on a large number of work units, and most of the residents go home from work on weekdays or rest at home on weekends during the evening peak periods. And the increased mixing of urban POIs does not have a noticeable effect.

5.4 Measurement results of single urban function and mixed urban functions

Furthermore, in order to verify that the residents’ taxi travel demand is better affected by the interaction of urban internal functions than by the single urban function, this paper takes tourist attraction POI as an example to demonstrate. Based on the previous 13 classifications of urban POIs, we compared the results of the GWR model constructed by the urban POIs (13) and taxi travel demand, as well as single tourist attraction POI and taxi travel demand (Tables 6 and 7 ).

https://doi.org/10.1371/journal.pone.0247431.t006

https://doi.org/10.1371/journal.pone.0247431.t007

It can be seen from Tables 6 and 7 that on weekdays and weekends, regardless of the three peak periods or the whole day, the adjustment R 2 values of the GWR model of urban POIs (13) are higher than those of the GWR model of single tourist attraction POI. And the AIC C values of the GWR model of urban POIs (13) are lower than those of the GWR model of single tourist attraction POI. It shows that the GWR model of urban POIs (13) has higher goodness of fit. Despite this, we further removed the single tourist attraction POI and constructed the GWR model based on the remaining urban POIs (12) and taxi travel demand. The results are shown in Table 8 .

https://doi.org/10.1371/journal.pone.0247431.t008

Comparing the results of Tables 6 – 8 , it is found that on weekdays and weekends, regardless of the three peak periods or the whole day, the adjustment R 2 values of the GWR model of urban POIs (13) are highest, followed by urban POIs (12), and single tourist attraction POI. The AIC C values of the GWR model of urban POIs (13) are lowest. And the AIC C values of the GWR model of single tourist attraction POI have the highest AIC C values. It indicates that the GWR model of urban POIs (13) is the most effective, followed by POIs (12), and single tourist attraction POI.

To sum up, the taxi travel demand, that is, the purpose of travel, which is largely influenced by the interaction of urban internal functions. Although the single function of the city has an impact on the taxi travel demand, the result of the single function is not ideal. It fully explains the importance of the connection between the multifunctional living environment and residents’ taxi travel demand.

6. Conclusions

With the rapid development of urbanization, the continuous growth of the income level of urban residents, and the popularity of the pursuit of a high-quality, convenient life and consumption, the demand for taxi travel continues to have great potential. Due to limited taxi resources and the uncertainty of residents’ daily activities, it is an urgent issue for governments to make relevant policies and measures to provide support for residents’ taxi travel. It is necessary to further explore the distribution of residents’ travel purposes, namely, the POIs of basic urban constituent units, and the relationship between POIs and residents’ travel needs. Therefore, this paper calculates and analyzes the mixed degree of functions within a city based on urban POI data. The kernel density estimation method is used to visualize the distribution of taxi travel demand. And the GWR model is applied to identify the spatial variation of the coefficient of the influence of the mixed degree of urban functions on the residents’ taxi travel demand in the main urban area of Xi’an. It also compares the effects of the single function and the mixed functions on taxi travel demand of the city. The results of the discussion and analysis can be summarized as follows.

First, in the main urban area of Xi’an City, the overall pattern of the mixed degree of urban functions is lowest outside the third ring road, and gradually increasing within the third ring road. Understanding these distribution characteristics can provide a reference for residents’ diversified travel purposes.

Second, in the main urban area of Xi’an, the taxi travel demand on weekends is higher than that on weekdays during the periods of 0:00–6:00, 12:00–14:00, and 17:30–24:00. And there is a high taxi travel demand during the evening peak (21:30–23:30) on weekdays and weekends. The management department can take these periods into account when carrying out dynamic adjustment of transport capacity, and formulate taxi capacity delivery measures in different periods.

Third, in the main urban area of Xi’an City, there are several hot spots with stable taxi demand during the morning, noon, and evening peak periods, that is, there is a fixed population but also some differences in time. For example, during the noon peak (12:30–14:30) and evening peak (21:30–23:30), the taxi travel demand around the Bell Tower, Xiaozhai, and the Exhibition Center is stable. For these hot spots of taxi travel demand, the taxi management department can allocate taxis reasonably. And encourage residents to stagger the peak travel periods when going to these places, so as to ensure the convenience and smooth travel of residents.

Fourth, in the main urban area of Xi’an, the east-west direction of Xi’an reveals a great difference in the influence of the mixed degree urban functions on the residents’ taxi travel demand compared with the north and south sides. In the north-east, south-east and north-west corner of the main urban area, the mixed degree of urban functions has the least impact on the residents’ taxi travel demand, and basically in inverse proportion. Near the Bell Tower, Xiaozhai, the Exhibition Center, and the High-Tech Industrial Park, where there is a high mixed degree of urban functions, and the residents’ taxi travel demand is the largest. With this information, the management department can consider the dynamic car allocation algorithm affected by the mixed degree of urban function when the taxi capacity is configured. Taxi drivers can also take into account the differences in temporal and spatial to attract passengers, so as to alleviate the traffic congestion and improve the operating efficiency of taxi drivers.

Fifth, the taxi travel demand is largely influenced by the interaction of the urban internal functions. Although the single function of the city has an impact on taxi travel demand, the result of the single function is not ideal. Therefore, in the process of urban planning, the optimal combinations of the basic units of urban space should be further explored.

7. Limitations and future work

Further research should address the deficiencies of this paper, which are as follows:

• The classification of urban POI data types in this paper is partly based on the needs of this study, and more research on the classification of urban POI data needs to be carried out.
• This paper takes the big city Xi’an as an example to research, which is different from small and medium-sized cities. In the future, we can carry out research on small and medium-sized cities to further verify our conclusions.
• This study focuses on the impact of the mixed degree of urban functions on the taxi travel demand, without considering factors such as road capacity and traffic congestion. The influence of such factors can be further considered in the future.

Supporting information

S1 file. poi data..

https://doi.org/10.1371/journal.pone.0247431.s001

S2 File. 11.4 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s002

S3 File. 11.5 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s003

S4 File. 11.6 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s004

S5 File. 11.7 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s005

S6 File. 11.8 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s006

S7 File. 11.9 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s007

S8 File. 11.10 taxi data.

https://doi.org/10.1371/journal.pone.0247431.s008

Acknowledgments

We thank those anonymous reviewers and the editor whose comments/suggestions helped improve and clarify this manuscript.

• View Article
• Google Scholar
• 3. 2018 Xi’an transport development annual report. Xi’an: 2018.
• 5. Geng Z, Shang D, Zhu Q, Wu Q, Han Y. Research on improved focused crawler and its application in food safety public opinion analysis. New York: Ieee; 2017. 2847–52 p.
• 6. Han J, Zhou Q, Han H. Research on Application of Reptilian Technology in Tax Management Achievements. IOP Conference Series: Earth and Environmental Science2019. p. 042021.
• 12. Bischoff J, Maciejewski M, Sohr A. Analysis of Berlin’s taxi services by exploring GPS traces. 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS)2015. p. 209–15.
• 15. Kamga C, Yazici MA, Singhal A. Hailing in the Rain: Temporal and Weather-Related Variations in Taxi Ridership and Taxi Demand-Supply Equilibrium. Transportation Research Board‟s 92nd Annual Meeting; 2013; Washington.
• 17. Jiang Y, Yan X. Discovering the Relationship between Travel Behavior and Land use: A Case Study of Beijing, China. 2019 4th International Conference on Electromechanical Control Technology and Transportation (ICECTT)2019. p. 219–24.
• 20. Kutner MH,Nachts CJ. Applied linear regression models: Higher Education Pressn; McGraw-Hill Education (Asia) Co; 2005.
• 27. Qian X, Zhan X, Ukkusuri SV. Characterizing Urban Dynamics Using Large Scale Taxicab Data: Springer International Publishing; 2015.
• PubMed/NCBI
• 36. Zheng Y, Liu Y, Yuan J, Xie X. Urban computing with taxicabs. ubiquitous computing; 2011.
• 39. Map G. 2018 Traffic Analysis Reports for Major Cities in China. Beijing: Gaode Map, 2018.
• 41. Krosche J, Boll S. The xPOI concept. location and context awareness; 2005.