a train after travelling 80kmph slows down

A train after travelling 50 km meet with an accident and then proceeds at 3/4th of its former speed and arrives at its destination 35 minutes late. Had an accident occurred 24 kms further, it would have reached destination only 25 minutes late. The speed of the train is ? 36 kmph 48 kmph 54 kmph 58 kmph

Train proceeds at 3/4 s where s is his usual speed means 1/4 decrease in the speed which will lead to 1/3 increase in the time. [ as s *t = d, speed is inversely proportional to time when distance is constant]. now, the main difference come in those 24 km and the change in difference of time = 35 - 25 = 10 m = 1 / 3 *t = 10 where t is the time required to cover the distance of (50 - 74) = 24 km t = 30 min = 0.5 hours speed of the train = 24 / (0.5) = 48 kmph..

A train after travelling 150 km meets with an accident and then proceeds at 3/5 of its former speed and arrives at its destination 8 hours late. Had the accident occurred 360 km further, it would have reached the destination 4 hours late. What is the total distance travelled by the train?

EXAMPLE 2.11 A train slows down from 80 kmh^(-1) with a uniform retardation of 2 ms^(-2). How long will it take to attain a speed of 20kmh^(-1) ? SOLUTION -1

Expert verified solution.

Acceleration Calculator

Easily calculate the acceleration, starting and final speed, or time to reach a given speed with this acceleration calculator. Supported metrics are meters per second, miles per hour, miles per second, km per hour, km per second, yards/feet per second and knots. Output is in meters per second squared and standard gravity ( g, g-units ).

Related calculators

• About the acceleration calculator

Standard Gravity

• Acceleration formula
• Equations for initial velocity, final velocity, and time
• Calculation examples

    About the acceleration calculator

This acceleration calculator is useful for any kind of vehicle or object: car, bus, train, bike, motorcycle, plane, ship, space craft, projectile, etc. due to the many different units supported. You need to know 3 of the 4: acceleration, initial speed, final speed and time (acceleration duration) to calculate the fourth.

The output is always in the input unit squared (e.g. km/h 2 ), meters per second squared (m/s 2 ) and standard gravity units ( g n , often just g ).

The calculator can be used to calculate deceleration as well, simply by entering a lower value for the final speed. It can be used to estimate the deceleration required to come to a full stop in a given number of seconds, for example, or the breaking path of a vehicle decelerating at a given rate.

g n is equal to 9.80665 m/s 2 and is the standard acceleration due to Earth's gravity according to the International Service of Weights and Measures [1][2] . The value of ɡ n is a nominal midrange value on Earth, originally based on the acceleration of a body in free fall at sea level at a geodetic latitude of 45°, the actual acceleration of free fall on Earth varies according to location.

The human body can handle a different amount of g-force depending on whether it is perpendicular to or along the spine. If perpendicular, many humans can endure 20g for about 10 seconds, 10g for a minute, and 6g for up to 10 minutes, without any ill effects. However, the human body deals much worse with vertical g-forces that are aligned with the spine. A typical person can handle 5g for a short duration without passing out, while trained pilots with suits and other equipment can withstand 9g for prolonged periods of time. Negative g-force is much harder to handle, with the limit being between -2g and -3g.

    Acceleration formula

The formula for acceleration expressed in terms of the initial velocity (speed), final velocity and the acceleration duration (time) is:

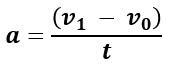
where a is the acceleration, v 0 is the starting velocity, v 1 is the final velocity, and t is the time (acceleration duration or t 1 - t 0 ). The resulting unit will depend on the units for both time and distance, so if your input was in miles and hours, the acceleration will be in miles/h 2 . If it was in meters and seconds, it would be in m/s 2 (meters per second squared). Remember to always have the time unit of the speed measure being the same as the duration measure.

    Equations for initial velocity, final velocity, and time

Variants of the formula above are used when solving for initial velocity, final velocity or time. The equation is to be rearranged in the following way depending on what is to be found:

• to find the initial velocity (v 0 ) : v 1 - a / t
• to find the final velocity (v 1 ) : v 0 + a / t
• to find the time (t) : (v 1 - v 0 ) / a

Initial velocity is often incorrectly referred to as initial speed , but the correct term is usually velocity since it represents the magnitude of a vector and therefore has direction. Speed, on the other hand, is a scalar value and does not indicate direction.

    Calculation examples

Example 1: If your car starts at 0 mph and accelerates to 60 miles per hour in 8 seconds, what is its average acceleration during these eight seconds? The answer is (60 mph - 0 mph) / 8s = (26.8224 m/s - 0 m/s) / 8s = 3.3528 m/s 2 (meters per second squared) average car acceleration. That would be 27,000 miles per hour squared.

Example 2: If a truck is travelling at 50 km/h and increases its velocity to 65 km per hour in 10 seconds, what is its acceleration? The answer is (65 kmph - 50 kmph) / 10s = (18.055 m/s - 13.888888 m/s) / 10s = 0.416667 m/s 2 (meters per second squared).

Example 3: If a ship is moving at 20 knots and you want to know how hard you should decelerate in order to reach a full stop in 30 seconds, you need to calculate (0 knots - 20 knots) / 30s = -33.76 ft/s / 30s = -1.1252 ft/s 2 or -0.342963 m/s 2 .

Example 4: A plane takes off at a certain speed and then accelerates for 2 minutes by 1.6 m/s 2 on average to reach cruising altitude and velocity which is 900 km/h. What is the initial speed / initial velocity of the plane? To calculate this, use the first variant of the acceleration formula and replace the known variables: 900 km/h - 1.6 m/s 2 · 2 min. After the necessary unit conversion we arrive at the solution: 250 m/s - 1.6 m/s 2 · 120 s = 250 m/s - 192 m/s = 58 m/s or ~209 km/h.

    References

1 NIST Special Publication 330 (2008) - "The International System of Units (SI)", edited by Barry N.Taylor and Ambler Thompson, p. 52

2 "The International System of Units" (SI) (2006, 8th ed.). Bureau international des poids et mesures pp. 142–143. ISBN 92-822-2213-6

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Acceleration Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/acceleration-calculator.php URL [Accessed Date: 11 Jun, 2024].

     Physics calculators

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 2 One-Dimensional Kinematics

11 2.5 Motion Equations for Constant Acceleration in One Dimension

• Calculate displacement of an object that is not acceleration, given initial position and velocity.
• Calculate final velocity of an accelerating object, given initial velocity, acceleration, and time.
• Calculate displacement and final position of an accelerating object, given initial position, initial velocity, time, and acceleration.

We might know that the greater the acceleration of, say, a car moving away from a stop sign, the greater the displacement in a given time. But we have not developed a specific equation that relates acceleration and displacement. In this section, we develop some convenient equations for kinematic relationships, starting from the definitions of displacement, velocity, and acceleration already covered.

Notation: t , x , v , a

First, let us make some simplifications in notation. Taking the initial time to be zero, as if time is measured with a stopwatch, is a great simplification. Since elapsed time is[latex]\boldsymbol{\Delta{t}={t_f}-{t_0}}[/latex], taking[latex]\boldsymbol{t_0=0}[/latex] means that[latex]\boldsymbol{\Delta{t}={t_f}}[/latex], the final time on the stopwatch. When initial time is taken to be zero, we use the subscript 0 to denote initial values of position and velocity. That is,[latex]\boldsymbol{x_0}[/latex] is the initial position and[latex]\boldsymbol{v_0}[/latex] is the initial velocity . We put no subscripts on the final values. That is,[latex]\boldsymbol{t}[/latex] is the final time ,[latex]\boldsymbol{x}[/latex] is the final position , and [latex]\boldsymbol{v}[/latex] is the final velocity . This gives a simpler expression for elapsed time—now,[latex]\boldsymbol{\Delta{t}=t}[/latex]. It also simplifies the expression for displacement, which is now[latex]\boldsymbol{\Delta{x}={x}-{x_0}}[/latex]. Also, it simplifies the expression for change in velocity, which is now[latex]\boldsymbol{\Delta{v}={v}-{v_0}}[/latex]. To summarize, using the simplified notation, with the initial time taken to be zero,

where the subscript 0 denotes an initial value and the absence of a subscript denotes a final value in whatever motion is under consideration.

We now make the important assumption that acceleration is constant . This assumption allows us to avoid using calculus to find instantaneous acceleration. Since acceleration is constant, the average and instantaneous accelerations are equal. That is,

so we use the symbol[latex]\textbf{a}[/latex]for acceleration at all times. Assuming acceleration to be constant does not seriously limit the situations we can study nor degrade the accuracy of our treatment. For one thing, acceleration is constant in a great number of situations. Furthermore, in many other situations we can accurately describe motion by assuming a constant acceleration equal to the average acceleration for that motion. Finally, in motions where acceleration changes drastically, such as a car accelerating to top speed and then braking to a stop, the motion can be considered in separate parts, each of which has its own constant acceleration.

SOLVING FOR DISPLACEMENT (Δ x ) AND FINAL POSITION ( x ) FROM AVERAGE VELOCITY WHEN ACCELERATION ( a ) IS CONSTANT

To get our first two new equations, we start with the definition of average velocity:

Substituting the simplified notation for[latex]\boldsymbol{\Delta{x}}[/latex]and[latex]\boldsymbol{\Delta{t}}[/latex]yields

Solving for[latex]\boldsymbol{x}[/latex]yields

where the average velocity is

The equation [latex]\boldsymbol{\bar{v}=}[/latex][latex]\boldsymbol{\frac{{v}_0+{v}}{2}}[/latex]reflects the fact that, when acceleration is constant,[latex]\boldsymbol{v}[/latex]is just the simple average of the initial and final velocities. For example, if you steadily increase your velocity (that is, with constant acceleration) from 30 to 60 km/h, then your average velocity during this steady increase is 45 km/h. Using the equation [latex]\boldsymbol{\bar{v}=}[/latex][latex]\boldsymbol{\frac{{v}_0+{v}}{2}}[/latex] to check this, we see that

which seems logical.

Example 1: Calculating Displacement: How Far does the Jogger Run?

A jogger runs down a straight stretch of road with an average velocity of 4.00 m/s for 2.00 min. What is his final position, taking his initial position to be zero?

Draw a sketch.

The final position[latex]\boldsymbol{x}[/latex]is given by the equation

To find[latex]\boldsymbol{x}[/latex], we identify the values of[latex]\boldsymbol{x_0}[/latex],[latex]\boldsymbol{\bar{v}}[/latex], and[latex]\boldsymbol{t}[/latex] from the statement of the problem and substitute them into the equation.

1. Identify the knowns.[latex]\boldsymbol{\bar{v}=4.00\textbf{ m/s}}[/latex],[latex]\boldsymbol{\Delta{t}=2.00\textbf{ min}}[/latex], and[latex]\boldsymbol{{x}_0=0\textbf{ m}}[/latex].

2. Enter the known values into the equation.

Velocity and final displacement are both positive, which means they are in the same direction.

The equation[latex]\boldsymbol{{x}={x}_0+\bar{v}{t}}[/latex]gives insight into the relationship between displacement, average velocity, and time. It shows, for example, that displacement is a linear function of average velocity. (By linear function, we mean that displacement depends on[latex]\boldsymbol{\bar{v}}[/latex] rather than on[latex]\boldsymbol{\bar{v}}[/latex]raised to some other power, such as[latex]\boldsymbol{\bar{v}^2}[/latex]. When graphed, linear functions look like straight lines with a constant slope.) On a car trip, for example, we will get twice as far in a given time if we average 90 km/h than if we average 45 km/h.

SOLVING FOR FINAL VELOCITY

We can derive another useful equation by manipulating the definition of acceleration.

Substituting the simplified notation for[latex]\boldsymbol{\Delta{v}}[/latex]and[latex]\boldsymbol{\Delta{t}}[/latex]gives us

Solving for[latex]\boldsymbol{v}[/latex]yields

Example 2: Calculating Final Velocity: An Airplane Slowing Down after Landing

An airplane lands with an initial velocity of 70.0 m/s and then decelerates at[latex]\boldsymbol{1.50\textbf{ m/s}^2}[/latex] for 40.0 s. What is its final velocity?

Draw a sketch. We draw the acceleration vector in the direction opposite the velocity vector because the plane is decelerating.

1. Identify the knowns.[latex]\boldsymbol{{v}_0=70.0\textbf{ m/s}}[/latex],[latex]\boldsymbol{{a}=-1.50\textbf{ m/s}^2}[/latex],[latex]\boldsymbol{{t}=40.0 \textbf{ s}}[/latex].

2. Identify the unknown. In this case, it is final velocity,[latex]\boldsymbol{v_f}[/latex].

3. Determine which equation to use. We can calculate the final velocity using the equation[latex]\boldsymbol{v=v_0+at}[/latex].

4. Plug in the known values and solve.

The final velocity is much less than the initial velocity, as desired when slowing down, but still positive. With jet engines, reverse thrust could be maintained long enough to stop the plane and start moving it backward. That would be indicated by a negative final velocity, which is not the case here.

In addition to being useful in problem solving, the equation[latex]\boldsymbol{v=v_0+at}[/latex] gives us insight into the relationships among velocity, acceleration, and time. From it we can see, for example, that

• final velocity depends on how large the acceleration is and how long it lasts
• if the acceleration is zero, then the final velocity equals the initial velocity[latex]\boldsymbol{(v=v_0)}[/latex], as expected (i.e., velocity is constant)
• if[latex]\boldsymbol{a}[/latex]is negative, then the final velocity is less than the initial velocity

(All of these observations fit our intuition, and it is always useful to examine basic equations in light of our intuition and experiences to check that they do indeed describe nature accurately.)

MAKING CONNECTIONS: REAL WORLD CONNECTION

An intercontinental ballistic missile (ICBM) has a larger average acceleration than the Space Shuttle and achieves a greater velocity in the first minute or two of flight (actual ICBM burn times are classified—short-burn-time missiles are more difficult for an enemy to destroy). But the Space Shuttle obtains a greater final velocity, so that it can orbit the earth rather than come directly back down as an ICBM does. The Space Shuttle does this by accelerating for a longer time.

SOLVING FOR FINAL POSITION WHEN VELOCITY IS NOT CONSTANT ( a ≠ 0 )

We can combine the equations above to find a third equation that allows us to calculate the final position of an object experiencing constant acceleration. We start with

Adding[latex]\boldsymbol{v_0}[/latex]to each side of this equation and dividing by 2 gives

Since[latex]\boldsymbol{\frac{v_0+v}{2}=\bar{v}}[/latex] for constant acceleration, then

Now we substitute this expression for[latex]\boldsymbol{\bar{v}}[/latex]into the equation for displacement,[latex]\boldsymbol{x=x_0+\bar{v}t}[/latex], yielding

Example 3: Calculating Displacement of an Accelerating Object: Dragsters

Dragsters can achieve average accelerations of[latex]\boldsymbol{26.0\textbf{ m/s}^2}[/latex]. Suppose such a dragster accelerates from rest at this rate for 5.56 s. How far does it travel in this time?

We are asked to find displacement, which is[latex]\boldsymbol{x}[/latex]if we take[latex]\boldsymbol{x_0}[/latex]to be zero. (Think about it like the starting line of a race. It can be anywhere, but we call it 0 and measure all other positions relative to it.) We can use the equation[latex]\boldsymbol{x=x_0+v_0t+\frac{1}{2}at^2}[/latex]once we identify[latex]\boldsymbol{v_0}[/latex],[latex]\boldsymbol{a}[/latex], and[latex]\boldsymbol{t}[/latex]from the statement of the problem.

1. Identify the knowns. Starting from rest means that[latex]\boldsymbol{v_0=0}[/latex],[latex]\boldsymbol{a}[/latex]is given as[latex]\boldsymbol{26.0 \textbf{m/s}^2}[/latex] and[latex]\boldsymbol{t}[/latex]is given as 5.56 s.

2. Plug the known values into the equation to solve for the unknown[latex]\textbf{x}[/latex]:

Since the initial position and velocity are both zero, this simplifies to

Substituting the identified values of[latex]\boldsymbol{a}[/latex]and[latex]\boldsymbol{t}[/latex]gives

If we convert 402 m to miles, we find that the distance covered is very close to one quarter of a mile, the standard distance for drag racing. So the answer is reasonable. This is an impressive displacement in only 5.56 s, but top-notch dragsters can do a quarter mile in even less time than this.

What else can we learn by examining the equation[latex]\boldsymbol{x=x_0+v_0t+\frac{1}{2}at^2}[/latex]? We see that:

• displacement depends on the square of the elapsed time when acceleration is not zero. In Example 3 , the dragster covers only one fourth of the total distance in the first half of the elapsed time
• if acceleration is zero, then the initial velocity equals average velocity[latex]\boldsymbol{(v_0=\bar{v})}[/latex]and[latex]\boldsymbol{x=x_0+v_0t+\frac{1}{2}at^2}[/latex]becomes[latex]\boldsymbol{x=x_0+v_0t}[/latex]

SOLVING FOR FINAL VELOCITY WHEN VELOCITY IS NOT CONSTANT ( a ≠ 0 )

A fourth useful equation can be obtained from another algebraic manipulation of previous equations.

If we solve[latex]\boldsymbol{v=v_0+at}[/latex]for[latex]\boldsymbol{t}[/latex], we get

Substituting this and[latex]\boldsymbol{\bar{v}=\frac{v_0+v}{2}}[/latex]into[latex]\boldsymbol{x=x_0+\bar{v}t}[/latex], we get

Example 4: Calculating Final Velocity: Dragsters

Calculate the final velocity of the dragster in Example 3 without using information about time.

The equation[latex]\boldsymbol{v^2=v_0^2+2a(x-x_0)}[/latex] is ideally suited to this task because it relates velocities, acceleration, and displacement, and no time information is required.

1. Identify the known values. We know that[latex]\boldsymbol{v_0=0}[/latex], since the dragster starts from rest. Then we note that[latex]\boldsymbol{x-x_0=402\textbf{ m}}[/latex] (this was the answer in Example 3 ). Finally, the average acceleration was given to be[latex]\boldsymbol{a=26.0\textbf{ m/s}^2}[/latex].

2. Plug the knowns into the equation[latex]\boldsymbol{v^2=v_0^2+2a(x-x_0)}[/latex]and solve for[latex]\boldsymbol{v}[/latex].

To get[latex]\textbf{v}[/latex], we take the square root:

145 m/s is about 522 km/h or about 324 mi/h, but even this breakneck speed is short of the record for the quarter mile. Also, note that a square root has two values; we took the positive value to indicate a velocity in the same direction as the acceleration.

An examination of the equation[latex]\boldsymbol{v^2=v_0^2+2a(x-x_0)}[/latex] can produce further insights into the general relationships among physical quantities:

• The final velocity depends on how large the acceleration is and the distance over which it acts
• For a fixed deceleration, a car that is going twice as fast doesn’t simply stop in twice the distance—it takes much further to stop. (This is why we have reduced speed zones near schools.)

Putting Equations Together

In the following examples, we further explore one-dimensional motion, but in situations requiring slightly more algebraic manipulation. The examples also give insight into problem-solving techniques. The box below provides easy reference to the equations needed.

SUMMARY OF KINEMATIC EQUATIONS(CONSTANT a )

Example 5: calculating displacement: how far does a car go when coming to a halt.

On dry concrete, a car can decelerate at a rate of[latex]\boldsymbol{7.00\textbf{ m/s}^2}[/latex], whereas on wet concrete it can decelerate at only[latex]\boldsymbol{5.00\textbf{ m/s}^2}[/latex]. Find the distances necessary to stop a car moving at 30.0 m/s (about 110 km/h) (a) on dry concrete and (b) on wet concrete. (c) Repeat both calculations, finding the displacement from the point where the driver sees a traffic light turn red, taking into account his reaction time of 0.500 s to get his foot on the brake.

In order to determine which equations are best to use, we need to list all of the known values and identify exactly what we need to solve for. We shall do this explicitly in the next several examples, using tables to set them off.

Solution for (a)

1. Identify the knowns and what we want to solve for. We know that[latex]\boldsymbol{v_0=30.0\textbf{ m/s}}[/latex];[latex]\boldsymbol{v=0}[/latex];[latex]\boldsymbol{a=-7.00\textbf{ m/s}^2}[/latex]([latex]\boldsymbol{a}[/latex] is negative because it is in a direction opposite to velocity). We take[latex]\boldsymbol{x_0}[/latex]to be 0. We are looking for displacement[latex]\boldsymbol{\Delta{x}}[/latex], or[latex]\boldsymbol{x-x_0}[/latex].

2. Identify the equation that will help up solve the problem. The best equation to use is

This equation is best because it includes only one unknown,[latex]\boldsymbol{x}[/latex]. We know the values of all the other variables in this equation. (There are other equations that would allow us to solve for[latex]\boldsymbol{x}[/latex], but they require us to know the stopping time,[latex]\boldsymbol{t}[/latex], which we do not know. We could use them but it would entail additional calculations.)

3. Rearrange the equation to solve for[latex]\textbf{x}[/latex].

4. Enter known values.

Solution for (b)

This part can be solved in exactly the same manner as Part A. The only difference is that the deceleration is[latex]\boldsymbol{-5.00\textbf{ m/s}^2}[/latex]. The result is

Solution for (c)

Once the driver reacts, the stopping distance is the same as it is in Parts A and B for dry and wet concrete. So to answer this question, we need to calculate how far the car travels during the reaction time, and then add that to the stopping time. It is reasonable to assume that the velocity remains constant during the driver’s reaction time.

1. Identify the knowns and what we want to solve for. We know that[latex]\boldsymbol{\bar{v}=30.0\textbf{ m/s}}[/latex];[latex]\boldsymbol{t_{reaction}=0.500\textbf{ s}}[/latex];[latex]\boldsymbol{a_{reaction}=0}[/latex]. We take[latex]\boldsymbol{x_{0-reaction}}[/latex] to be 0. We are looking for[latex]\boldsymbol{x_{reaction}}[/latex].

2. Identify the best equation to use.

[latex]\boldsymbol{x=x_0+\bar{v}t}[/latex]works well because the only unknown value is[latex]\boldsymbol{x}[/latex], which is what we want to solve for.

3. Plug in the knowns to solve the equation.

This means the car travels 15.0 m while the driver reacts, making the total displacements in the two cases of dry and wet concrete 15.0 m greater than if he reacted instantly.

4. Add the displacement during the reaction time to the displacement when braking.

The displacements found in this example seem reasonable for stopping a fast-moving car. It should take longer to stop a car on wet rather than dry pavement. It is interesting that reaction time adds significantly to the displacements. But more important is the general approach to solving problems. We identify the knowns and the quantities to be determined and then find an appropriate equation. There is often more than one way to solve a problem. The various parts of this example can in fact be solved by other methods, but the solutions presented above are the shortest.

Example 6: Calculating Time: A Car Merges into Traffic

Suppose a car merges into freeway traffic on a 200-m-long ramp. If its initial velocity is 10.0 m/s and it accelerates at[latex]\boldsymbol{2.00\textbf{ m/s}^2}[/latex], how long does it take to travel the 200 m up the ramp? (Such information might be useful to a traffic engineer.)

We are asked to solve for the time[latex]\boldsymbol{t}[/latex]. As before, we identify the known quantities in order to choose a convenient physical relationship (that is, an equation with one unknown,[latex]\boldsymbol{t}[/latex]).

1. Identify the knowns and what we want to solve for. We know that[latex]\boldsymbol{v_0=10\textbf{ m/s}}[/latex];[latex]\boldsymbol{a=2.00\textbf{ m/s}^2}[/latex]; and[latex]\boldsymbol{x=200\textbf{ m}}[/latex].

2. We need to solve for[latex]\boldsymbol{t}[/latex]. Choose the best equation.[latex]\boldsymbol{x=x_0+v_0t+\frac{1}{2}at^2}[/latex] works best because the only unknown in the equation is the variable[latex]\boldsymbol{t}[/latex] for which we need to solve.

3. We will need to rearrange the equation to solve for[latex]\boldsymbol{t}[/latex]. In this case, it will be easier to plug in the knowns first.

4. Simplify the equation. The units of meters (m) cancel because they are in each term. We can get the units of seconds (s) to cancel by taking[latex]\boldsymbol{\textbf{t}=\textbf{t s}}[/latex], where[latex]\textbf{t}[/latex] is the magnitude of time and s is the unit. Doing so leaves

5. Use the quadratic formula to solve for[latex]\boldsymbol{t}[/latex] .

(a) Rearrange the equation to get 0 on one side of the equation.

This is a quadratic equation of the form

where the constants are[latex]\boldsymbol{a=1.00\textbf{, }b=10.0\textbf{, and }c=-200}[/latex].

(b) Its solutions are given by the quadratic formula:

This yields two solutions for[latex]\boldsymbol{t}[/latex], which are

In this case, then, the time is[latex]\boldsymbol{t=t}[/latex] in seconds, or

A negative value for time is unreasonable, since it would mean that the event happened 20 s before the motion began. We can discard that solution. Thus,

Whenever an equation contains an unknown squared, there will be two solutions. In some problems both solutions are meaningful, but in others, such as the above, only one solution is reasonable. The 10.0 s answer seems reasonable for a typical freeway on-ramp.

With the basics of kinematics established, we can go on to many other interesting examples and applications. In the process of developing kinematics, we have also glimpsed a general approach to problem solving that produces both correct answers and insights into physical relationships. Chapter 2.6 Problem-Solving Basics discusses problem-solving basics and outlines an approach that will help you succeed in this invaluable task.

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT–BREAKING NEWS

We have been using SI units of meters per second squared to describe some examples of acceleration or deceleration of cars, runners, and trains. To achieve a better feel for these numbers, one can measure the braking deceleration of a car doing a slow (and safe) stop. Recall that, for average acceleration,[latex]\boldsymbol{\bar{a}=\Delta{v}/\Delta{t}}[/latex]. While traveling in a car, slowly apply the brakes as you come up to a stop sign. Have a passenger note the initial speed in miles per hour and the time taken (in seconds) to stop. From this, calculate the deceleration in miles per hour per second. Convert this to meters per second squared and compare with other decelerations mentioned in this chapter. Calculate the distance traveled in braking.

Check Your Understanding

1: A manned rocket accelerates at a rate of[latex]\boldsymbol{20\textbf{m/s}^2}[/latex]during launch. How long does it take the rocket to reach a velocity of 400 m/s?

Section Summary

• To simplify calculations we take acceleration to be constant, so that[latex]\boldsymbol{\bar{a}=a}[/latex] at all times.
• We also take initial time to be zero.
• Initial position and velocity are given a subscript 0; final values have no subscript. Thus,

[latex]\begin{array}{lcl} \boldsymbol{\Delta{t}} & = & \boldsymbol{t} \\ \boldsymbol{\Delta{x}} & = & \boldsymbol{x-x_0} \\ \boldsymbol{\Delta{v}} & = & \boldsymbol{v-v_0} \end{array}[/latex][latex]\rbrace[/latex]

• The following kinematic equations for motion with constant[latex]\boldsymbol{a}[/latex]are useful: [latex]\boldsymbol{x=x_0+\bar{v}t}[/latex] [latex]\boldsymbol{\bar{v}=}[/latex][latex]\boldsymbol{\frac{v_0+v}{2}}[/latex] [latex]\boldsymbol{v=v_0+at}[/latex] [latex]\boldsymbol{x=x_0+v_0t+}[/latex][latex]\boldsymbol{\frac{1}{2}}[/latex][latex]\boldsymbol{at^2}[/latex] [latex]\boldsymbol{v^2=v_0^2+2a(x-x_0)}[/latex]
• In vertical motion,[latex]\boldsymbol{y}[/latex]is substituted for[latex]\boldsymbol{x}[/latex].

Problems & Exercises

1: An Olympic-class sprinter starts a race with an acceleration of[latex]\boldsymbol{4.50\textbf{ m/s}^2}[/latex]. (a) What is her speed 2.40 s later? (b) Sketch a graph of her position vs. time for this period.

2: A well-thrown ball is caught in a well-padded mitt. If the deceleration of the ball is[latex]\boldsymbol{2.10\times10^4\textbf{ m/s}^2}[/latex], and 1.85 ms[latex]\boldsymbol{(1\textbf{ ms}=10^{-3}\textbf{ s})}[/latex]elapses from the time the ball first touches the mitt until it stops, what was the initial velocity of the ball?

3: A bullet in a gun is accelerated from the firing chamber to the end of the barrel at an average rate of[latex]\boldsymbol{6.20\times10^5\textbf{ m/s}^2}[/latex]for[latex]\boldsymbol{8.10\times10^{-4}\textbf{ s}}[/latex]. What is its muzzle velocity (that is, its final velocity)?

4: (a) A light-rail commuter train accelerates at a rate of[latex]\boldsymbol{1.35\textbf{ m/s}^2}[/latex]. How long does it take to reach its top speed of 80.0 km/h, starting from rest? (b) The same train ordinarily decelerates at a rate of[latex]\boldsymbol{1.65\textbf{ m/s}^2}[/latex]. How long does it take to come to a stop from its top speed? (c) In emergencies the train can decelerate more rapidly, coming to rest from 80.0 km/h in 8.30 s. What is its emergency deceleration in[latex]\boldsymbol{\textbf{m/s}^2}[/latex]?

5: While entering a freeway, a car accelerates from rest at a rate of[latex]\boldsymbol{2.40\textbf{ m/s}^2}[/latex]for 12.0 s. (a) Draw a sketch of the situation. (b) List the knowns in this problem. (c) How far does the car travel in those 12.0 s? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, check your units, and discuss whether the answer is reasonable. (d) What is the car’s final velocity? Solve for this unknown in the same manner as in part (c), showing all steps explicitly.

6: At the end of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of[latex]\boldsymbol{2.00\textbf{ m/s}^2}[/latex]. (a) How far does she travel in the next 5.00 s? (b) What is her final velocity? (c) Evaluate the result. Does it make sense?

7:  Professional Application:

Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart. (a) Make a sketch of the situation. (b) List the knowns in this problem. (c) How long does the acceleration take? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units. (d) Is the answer reasonable when compared with the time for a heartbeat?

8: In a slap shot, a hockey player accelerates the puck from a velocity of 8.00 m/s to 40.0 m/s in the same direction. If this shot takes[latex]\boldsymbol{3.33\times10^{-2}\textbf{ s}}[/latex], calculate the distance over which the puck accelerates.

9: A powerful motorcycle can accelerate from rest to 26.8 m/s (100 km/h) in only 3.90 s. (a) What is its average acceleration? (b) How far does it travel in that time?

10: Freight trains can produce only relatively small accelerations and decelerations. (a) What is the final velocity of a freight train that accelerates at a rate of[latex]\boldsymbol{0.0500\textbf{ m/s}^2}[/latex]for 8.00 min, starting with an initial velocity of 4.00 m/s? (b) If the train can slow down at a rate of[latex]\boldsymbol{0.550\textbf{ m/s}^2}[/latex], how long will it take to come to a stop from this velocity? (c) How far will it travel in each case?

11: A fireworks shell is accelerated from rest to a velocity of 65.0 m/s over a distance of 0.250 m. (a) How long did the acceleration last? (b) Calculate the acceleration.

12: A swan on a lake gets airborne by flapping its wings and running on top of the water. (a) If the swan must reach a velocity of 6.00 m/s to take off and it accelerates from rest at an average rate of[latex]\boldsymbol{0.350\textbf{ m/s}^2}[/latex], how far will it travel before becoming airborne? (b) How long does this take?

13:  Professional Application:

A woodpecker’s brain is specially protected from large decelerations by tendon-like attachments inside the skull. While pecking on a tree, the woodpecker’s head comes to a stop from an initial velocity of 0.600 m/s in a distance of only 2.00 mm. (a) Find the acceleration in[latex]\boldsymbol{\textbf{m/s}^2}[/latex]and in multiples of[latex]\boldsymbol{g\:(g=9.80\textbf{ m/s}^2)}[/latex]. (b) Calculate the stopping time. (c) The tendons cradling the brain stretch, making its stopping distance 4.50 mm (greater than the head and, hence, less deceleration of the brain). What is the brain’s deceleration, expressed in multiples of[latex]\boldsymbol{g}[/latex]?

14: An unwary football player collides with a padded goalpost while running at a velocity of 7.50 m/s and comes to a full stop after compressing the padding and his body 0.350 m. (a) What is his deceleration? (b) How long does the collision last?

15: In World War II, there were several reported cases of airmen who jumped from their flaming airplanes with no parachute to escape certain death. Some fell about 20,000 feet (6000 m), and some of them survived, with few life-threatening injuries. For these lucky pilots, the tree branches and snow drifts on the ground allowed their deceleration to be relatively small. If we assume that a pilot’s speed upon impact was 123 mph (54 m/s), then what was his deceleration? Assume that the trees and snow stopped him over a distance of 3.0 m.

16: Consider a grey squirrel falling out of a tree to the ground. (a) If we ignore air resistance in this case (only for the sake of this problem), determine a squirrel’s velocity just before hitting the ground, assuming it fell from a height of 3.0 m. (b) If the squirrel stops in a distance of 2.0 cm through bending its limbs, compare its deceleration with that of the airman in the previous problem.

17: An express train passes through a station. It enters with an initial velocity of 22.0 m/s and decelerates at a rate of[latex]\boldsymbol{0.150\textbf{ m/s}^2}[/latex] as it goes through. The station is 210 m long. (a) How long is the nose of the train in the station? (b) How fast is it going when the nose leaves the station? (c) If the train is 130 m long, when does the end of the train leave the station? (d) What is the velocity of the end of the train as it leaves?

18: Dragsters can actually reach a top speed of 145 m/s in only 4.45 s—considerably less time than given in Example 3 and Example 4 . (a) Calculate the average acceleration for such a dragster. (b) Find the final velocity of this dragster starting from rest and accelerating at the rate found in (a) for 402 m (a quarter mile) without using any information on time. (c) Why is the final velocity greater than that used to find the average acceleration? Hint : Consider whether the assumption of constant acceleration is valid for a dragster. If not, discuss whether the acceleration would be greater at the beginning or end of the run and what effect that would have on the final velocity.

19: A bicycle racer sprints at the end of a race to clinch a victory. The racer has an initial velocity of 11.5 m/s and accelerates at the rate of[latex]\boldsymbol{0.500\textbf{ m/s}^2}[/latex]for 7.00 s. (a) What is his final velocity? (b) The racer continues at this velocity to the finish line. If he was 300 m from the finish line when he started to accelerate, how much time did he save? (c) One other racer was 5.00 m ahead when the winner started to accelerate, but he was unable to accelerate, and traveled at 11.8 m/s until the finish line. How far ahead of him (in meters and in seconds) did the winner finish?

20: In 1967, New Zealander Burt Munro set the world record for an Indian motorcycle, on the Bonneville Salt Flats in Utah, with a maximum speed of 183.58 mi/h. The one-way course was 5.00 mi long. Acceleration rates are often described by the time it takes to reach 60.0 mi/h from rest. If this time was 4.00 s, and Burt accelerated at this rate until he reached his maximum speed, how long did it take Burt to complete the course?

21: (a) A world record was set for the men’s 100-m dash in the 2008 Olympic Games in Beijing by Usain Bolt of Jamaica. Bolt “coasted” across the finish line with a time of 9.69 s. If we assume that Bolt accelerated for 3.00 s to reach his maximum speed, and maintained that speed for the rest of the race, calculate his maximum speed and his acceleration. (b) During the same Olympics, Bolt also set the world record in the 200-m dash with a time of 19.30 s. Using the same assumptions as for the 100-m dash, what was his maximum speed for this race?

1: To answer this, choose an equation that allows you to solve for time[latex]\boldsymbol{t}[/latex], given only[latex]\boldsymbol{a}[/latex],[latex]\boldsymbol{v_0}[/latex], and[latex]\boldsymbol{v}[/latex].

Rearrange to solve for[latex]\boldsymbol{t}[/latex] .

(a)[latex]\boldsymbol{10.8\textbf{ m/s}}[/latex]

(a)[latex]\boldsymbol{16.5\textbf{ s}}[/latex]

(b)[latex]\boldsymbol{13.5\textbf{ s}}[/latex]

(c)[latex]\boldsymbol{-2.68\textbf{ m/s}^2}[/latex]

(a)[latex]\boldsymbol{20.0\textbf{ m}}[/latex]

(b)[latex]\boldsymbol{-1.00\textbf{ m/s}}[/latex]

(c) This result does not really make sense. If the runner starts at 9.00 m/s and decelerates at[latex]\boldsymbol{2.00\textbf{ m/s}^2}[/latex], then she will have stopped after 4.50 s. If she continues to decelerate, she will be running backwards.

(a)[latex]\boldsymbol{28.0\textbf{ m/s}}[/latex]

(b)[latex]\boldsymbol{50.9\textbf{ s}}[/latex]

(c) 7.68 km to accelerate and 713 m to decelerate

(a)[latex]\boldsymbol{51.4\textbf{ m}}[/latex]

(b)[latex]\boldsymbol{17.1\textbf{ s}}[/latex]

(a)[latex]\boldsymbol{-80.4\textbf{ m/s}^2}[/latex]

(b)[latex]\boldsymbol{9.33\times10^{-2}\textbf{ s}}[/latex]

(a)[latex]\boldsymbol{7.7\textbf{ m/s}}[/latex]

(b)[latex]\boldsymbol{-15\times10^2\textbf{ m/s}^2}[/latex]. This is about 3 times the deceleration of the pilots, who were falling from thousands of meters high!

(a)[latex]\boldsymbol{32.6\textbf{ m/s}^2}[/latex]

(b)[latex]\boldsymbol{162\textbf{ m/s}}[/latex]

(c)[latex]\boldsymbol{v>v_{max}}[/latex], because the assumption of constant acceleration is not valid for a dragster. A dragster changes gears, and would have a greater acceleration in first gear than second gear than third gear, etc. The acceleration would be greatest at the beginning, so it would not be accelerating at[latex]\boldsymbol{32.6\textbf{ m/s}^2}[/latex]during the last few meters, but substantially less, and the final velocity would be less than 162 m/s.

(a)[latex]\boldsymbol{v=12.2\textbf{ m/s}}[/latex];[latex]\boldsymbol{a=4.07\textbf{ m/s}^2}[/latex]

(b)[latex]\boldsymbol{v=11.2\textbf{ m/s}}[/latex]

College Physics: OpenStax Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

A train travelling at 100 km/h slows down with a uniform deceleration of 0.600 m/s. How long does it take to stop?

Impact of this question

PHYS101: Introduction to Mechanics

Acceleration

Read this text. Pay attention to the examples which show how to solve equations of motion. These include how to calculate displacement, given average velocity and time, and how to calculate final velocity, given initial velocity, acceleration, and time.

Example 2.5 Calculate Acceleration: A Subway Train Slowing Down

Now suppose that at the end of its trip, the train in Figure 2.18(a) slows to a stop from a speed of 30.0 km/h in 8.00 s. What is its average acceleration while stopping?

Figure 2.20

In this case, the train is decelerating and its acceleration is negative because it is toward the left. As in the previous example, we must find the change in velocity and the change in time and then solve for acceleration.

4. Convert the units to meters and seconds.

The minus sign indicates that acceleration is to the left. This sign is reasonable because the train initially has a positive velocity in this problem, and a negative acceleration would oppose the motion. Again, acceleration is in the same direction as the change in velocity, which is negative here. This acceleration can be called a deceleration because it has a direction opposite to the velocity.

 a train slows down from 80 kilometer per hour with a uniform retardation of 2 meters per second.How long will it take to attain a speed of 2

a train slows down from 80 kilometer per hour with a uniform retardation of 2 meters per second.How long will it take to attain a speed of 20 kilometers per hour?

0 users composing answers..

Best answer  .

I am not sure if you want me to do this with calculus or with physics formulas.

I'll do it with physics formula.

$$\\u=80km/hour\;=\frac{80000}{60*60}m/sec = \frac{200}{3*3}m/sec= \frac{200}{9}m/sec\\\\ v=20km/hour\;=\frac{20000}{60*60}m/sec = \frac{50}{9}m/sec\\\\ a=-2m/s^2\\\\ find\;t\\\\ v=u+at\\\\ \frac{50}{9}=\frac{200}{9}+-2t\\\\ \frac{-250}{9}=-2t\\\\ \frac{250}{18}=t\\\\ t=13.9\;sec \qquad \mbox{to nearest one tenth of a second}\\\\$$

1 +0 Answers

3 online users.

Sticky Topics

Stopping Distance Calculator

Table of contents

Even if you're not a driver, you'll surely find the stopping distance calculator interesting. From the moment you spot a potentially dangerous situation to the moment when the car comes to a complete stop, it travels a certain distance. You can use this stopping distance calculator to find out how far your car travels in that time, depending on your speed, the slope of the road, and weather conditions.

In this text, we will clarify the difference between the stopping distance and the braking distance. We will also explain how to calculate the stopping distance according to AASHTO (the American Association of State Highway and Transportation Officials).

Stopping and braking distance

Imagine that you are driving your car on a regular street. Suddenly, you notice a child dart out across the street ahead of you. What happens during the next few stressful seconds?

First of all, some time will pass between the event happening and you perceiving it. This period is called the perception time . During this time, the car continues to move with the same speed as before, approaching the child on the road.

You might think that, as soon as you perceive the event, you hit the brake immediately, but there is always a small delay between the moment you notice the danger ahead and the instant in which you actually start to decelerate. This delay is called the reaction time . The car is still moving with the same speed.

After you start braking, the car will move slower and slower towards the child until it comes to a stop. The distance traveled from the moment you first hit the brake until you come to a complete stop is called the braking distance . The stopping distance , on the other hand, is the total distance traveled since the event began - the sum of distance travelled during perception, reaction, and braking time.

How do I calculate the stopping distance?

The AASHTO stopping distance formula is as follows:

s = (0.278 × t × v) + v² / (254 × (f + G))

• s – Stopping distance in meters;
• t – Perception-reaction time in seconds;
• v – Speed of the car in km/h;
• G – Grade (slope) of the road, expressed as a decimal. Positive for an uphill grade and negative for a downhill road; and
• f – Coefficient of friction between the tires and the road. It is assumed to be 0.7 on a dry road and between 0.3 and 0.4 on a wet road.

This formula is taken from the book "A Policy on Geometric Design of Highways and Streets". It is commonly used in road design for establishing the minimum stopping sight distance required on a given road. With correct parameters, it's a perfect equation for the accurate calculation of the stopping distance of your car. Clearly, it's different than the typical formula used in the speed calculator .

Most of the parameters in the formula above are easy to determine. You can have a big problem, though, when you try to estimate the perception-reaction time. We'll discuss it now.

What is the driver's perception-reaction time?

AASHTO recommends the value of 2.5 seconds to ensure that virtually every driver will manage to react within that time. In reality, many drivers are able to hit the brake much faster. You can use the following values as a rule of thumb:

• 1 second – A keen and alert driver;
• 1.5 seconds – An average driver;
• 2 seconds – A tired driver or an older person; and
• 2.5 seconds – The worst-case scenario. It is highly probable that even elderly or intoxicated drivers will manage to react within 2.5 seconds.

Calculating the stopping distance: an example

To determine the stopping distance of your car, follow the steps below.

Determine your speed. Let's assume that you're driving on a highway at a speed of 120 km/h.

Decide on your perception-reaction time. Let's say that you had a good night's sleep (with the help of the sleep calculator ) before hitting the road but have been driving for some time now and are not as alert as you could be. You can set your perception-reaction time to 1.5 seconds.

Input the slope of the road. If it is flat, you can just enter 0%.

Is the road wet or dry? Let's assume it just rained. With a speed of 120 km/h, our braking distance calculator gives us a friction coefficient of 0.27.

Input all parameters into the AASHTO equation:

s = (0.278 × 1.5 × 120) + 120² / (254 × (0.27 + 0))

s = 50 + 14400 / 68.6

s = 50 + 210

Your car will travel 260 meters before it comes to a stop.

💡 Being able to stop in time is crucial to road safety. If you visit the car crash calculator , you can see the potential impact of a collision.

What is the stopping distance on a dry road?

On a dry road the stopping distances are the following:

What is the stopping distance on a wet road?

On a wet road the stopping distances are the following:

What is the stopping distance for a car traveling at 50 kph?

The answer is a bit less than 50 m . To get this result:

We assume the road is flat and dry .

Moreover, we assume an average perception-reaction time of 2.5 seconds.

We apply the stopping distance formula, which (under our assumptions) reads:

s = (0.695 × v) + (v² / 177.8) .

Here, v denotes the car's speed in km/h.

Plugging in v = 50 , we get 48.81 m .

Vehicle speed

Perception-reaction time

Road grade (slope)

Positive if uphill, negative if downhill.

The road is... 

Friction coefficient

Stopping distance

.css-slt4t3.css-slt4t3{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-slt4t3.css-slt4t3:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-slt4t3 .js-external-link-button.link-like,.css-slt4t3 .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-slt4t3 .js-external-link-button.link-like:hover,.css-slt4t3 .js-external-link-anchor:hover,.css-slt4t3 .js-external-link-button.link-like:active,.css-slt4t3 .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-slt4t3 .js-external-link-button.link-like:focus-visible,.css-slt4t3 .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-slt4t3 p,.css-slt4t3 div{margin:0px;display:block;}.css-slt4t3 pre{margin:0px;display:block;}.css-slt4t3 pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-slt4t3 pre:not(:first-child){padding-top:8px;}.css-slt4t3 ul,.css-slt4t3 ol{display:block margin:0px;padding-left:20px;}.css-slt4t3 ul li,.css-slt4t3 ol li{padding-top:8px;}.css-slt4t3 ul ul,.css-slt4t3 ol ul,.css-slt4t3 ul ol,.css-slt4t3 ol ol{padding-top:0px;}.css-slt4t3 ul:not(:first-child),.css-slt4t3 ol:not(:first-child){padding-top:4px;} .css-4okk7a{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-4okk7a code,.css-4okk7a kbd,.css-4okk7a pre,.css-4okk7a samp{font-family:monospace;}.css-4okk7a code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-4okk7a figcaption,.css-4okk7a caption{text-align:center;}.css-4okk7a figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-4okk7a h3{font-size:1.75rem;}.css-4okk7a h4{font-size:1.5rem;}.css-4okk7a .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-4okk7a .mathBlock .katex{font-size:24px;text-align:left;}.css-4okk7a .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-4okk7a .videoBlock,.css-4okk7a .imageBlock{margin-bottom:16px;}.css-4okk7a .imageBlock__image-align--left,.css-4okk7a .videoBlock__video-align--left{float:left;}.css-4okk7a .imageBlock__image-align--right,.css-4okk7a .videoBlock__video-align--right{float:right;}.css-4okk7a .imageBlock__image-align--center,.css-4okk7a .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-4okk7a .imageBlock__image-align--none,.css-4okk7a .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-4okk7a .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-4okk7a .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-4okk7a .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-4okk7a .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-4okk7a .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-4okk7a .katex .katex-version::after{content:'0.13.13';}.css-4okk7a .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-4okk7a .katex .katex-html>.newline{display:block;}.css-4okk7a .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-4okk7a .katex .strut{display:inline-block;}.css-4okk7a .katex .textbf{font-weight:bold;}.css-4okk7a .katex .textit{font-style:italic;}.css-4okk7a .katex .textrm{font-family:KaTeX_Main;}.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .texttt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-4okk7a .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-4okk7a .katex .mathrm{font-style:normal;}.css-4okk7a .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-4okk7a .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-4okk7a .katex .amsrm{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathbb,.css-4okk7a .katex .textbb{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-4okk7a .katex .mathfrak,.css-4okk7a .katex .textfrak{font-family:KaTeX_Fraktur;}.css-4okk7a .katex .mathtt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathscr,.css-4okk7a .katex .textscr{font-family:KaTeX_Script;}.css-4okk7a .katex .mathsf,.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .mathboldsf,.css-4okk7a .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-4okk7a .katex .mathitsf,.css-4okk7a .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-4okk7a .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-4okk7a .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-4okk7a .katex .vlist-r{display:table-row;}.css-4okk7a .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-4okk7a .katex .vlist>span{display:block;height:0;position:relative;}.css-4okk7a .katex .vlist>span>span{display:inline-block;}.css-4okk7a .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-4okk7a .katex .vlist-t2{margin-right:-2px;}.css-4okk7a .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-4okk7a .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-4okk7a .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-4okk7a .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-4okk7a .katex .msupsub{text-align:left;}.css-4okk7a .katex .mfrac>span>span{text-align:center;}.css-4okk7a .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .mfrac .frac-line,.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline,.css-4okk7a .katex .hdashline,.css-4okk7a .katex .rule{min-height:1px;}.css-4okk7a .katex .mspace{display:inline-block;}.css-4okk7a .katex .llap,.css-4okk7a .katex .rlap,.css-4okk7a .katex .clap{width:0;position:relative;}.css-4okk7a .katex .llap>.inner,.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{position:absolute;}.css-4okk7a .katex .llap>.fix,.css-4okk7a .katex .rlap>.fix,.css-4okk7a .katex .clap>.fix{display:inline-block;}.css-4okk7a .katex .llap>.inner{right:0;}.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{left:0;}.css-4okk7a .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-4okk7a .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-4okk7a .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-4okk7a .katex .sizing.reset-size1.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-4okk7a .katex .sizing.reset-size1.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size1.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-4okk7a .katex .sizing.reset-size1.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size1.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size1.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-4okk7a .katex .sizing.reset-size1.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size1.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size1.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-4okk7a .katex .sizing.reset-size1.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-4okk7a .katex .sizing.reset-size1.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-4okk7a .katex .sizing.reset-size2.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size2.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-4okk7a .katex .sizing.reset-size2.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-4okk7a .katex .sizing.reset-size2.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size2.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size2.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-4okk7a .katex .sizing.reset-size2.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-4okk7a .katex .sizing.reset-size2.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size2.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size2.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-4okk7a .katex .sizing.reset-size2.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-4okk7a .katex .sizing.reset-size3.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-4okk7a .katex .sizing.reset-size3.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-4okk7a .katex .sizing.reset-size3.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-4okk7a .katex .sizing.reset-size3.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-4okk7a .katex .sizing.reset-size3.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-4okk7a .katex .sizing.reset-size3.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-4okk7a .katex .sizing.reset-size3.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-4okk7a .katex .sizing.reset-size3.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-4okk7a .katex .sizing.reset-size3.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-4okk7a .katex .sizing.reset-size4.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size4.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size4.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-4okk7a .katex .sizing.reset-size4.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-4okk7a .katex .sizing.reset-size4.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-4okk7a .katex .sizing.reset-size4.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-4okk7a .katex .sizing.reset-size4.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size4.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size4.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-4okk7a .katex .sizing.reset-size4.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-4okk7a .katex .sizing.reset-size4.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-4okk7a .katex .sizing.reset-size5.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size5.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size5.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-4okk7a .katex .sizing.reset-size5.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-4okk7a .katex .sizing.reset-size5.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-4okk7a .katex .sizing.reset-size5.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-4okk7a .katex .sizing.reset-size5.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size5.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size5.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-4okk7a .katex .sizing.reset-size5.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-4okk7a .katex .sizing.reset-size5.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-4okk7a .katex .sizing.reset-size6.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size6.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-4okk7a .katex .sizing.reset-size6.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-4okk7a .katex .sizing.reset-size6.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-4okk7a .katex .sizing.reset-size6.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-4okk7a .katex .sizing.reset-size6.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-4okk7a .katex .sizing.reset-size6.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size6.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size6.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-4okk7a .katex .sizing.reset-size6.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-4okk7a .katex .sizing.reset-size6.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-4okk7a .katex .sizing.reset-size7.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size7.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size7.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-4okk7a .katex .sizing.reset-size7.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size7.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size7.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size7.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-4okk7a .katex .sizing.reset-size7.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size7.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size7.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-4okk7a .katex .sizing.reset-size7.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-4okk7a .katex .sizing.reset-size8.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size8.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size8.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-4okk7a .katex .sizing.reset-size8.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size8.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size8.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size8.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size8.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-4okk7a .katex .sizing.reset-size8.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size8.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-4okk7a .katex .sizing.reset-size8.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-4okk7a .katex .sizing.reset-size9.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-4okk7a .katex .sizing.reset-size9.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size9.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-4okk7a .katex .sizing.reset-size9.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-4okk7a .katex .sizing.reset-size9.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-4okk7a .katex .sizing.reset-size9.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-4okk7a .katex .sizing.reset-size9.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size9.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size9.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-4okk7a .katex .sizing.reset-size9.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-4okk7a .katex .sizing.reset-size9.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-4okk7a .katex .sizing.reset-size10.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-4okk7a .katex .sizing.reset-size10.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-4okk7a .katex .sizing.reset-size10.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-4okk7a .katex .sizing.reset-size10.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-4okk7a .katex .sizing.reset-size10.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-4okk7a .katex .sizing.reset-size10.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-4okk7a .katex .sizing.reset-size10.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-4okk7a .katex .sizing.reset-size10.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-4okk7a .katex .sizing.reset-size10.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-4okk7a .katex .sizing.reset-size10.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-4okk7a .katex .sizing.reset-size10.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-4okk7a .katex .sizing.reset-size11.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-4okk7a .katex .sizing.reset-size11.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-4okk7a .katex .sizing.reset-size11.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-4okk7a .katex .sizing.reset-size11.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-4okk7a .katex .sizing.reset-size11.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-4okk7a .katex .sizing.reset-size11.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-4okk7a .katex .sizing.reset-size11.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-4okk7a .katex .sizing.reset-size11.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-4okk7a .katex .sizing.reset-size11.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-4okk7a .katex .sizing.reset-size11.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-4okk7a .katex .sizing.reset-size11.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-4okk7a .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-4okk7a .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-4okk7a .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-4okk7a .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-4okk7a .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-4okk7a .katex .delimcenter{position:relative;}.css-4okk7a .katex .op-symbol{position:relative;}.css-4okk7a .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-4okk7a .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-4okk7a .katex .op-limits>.vlist-t{text-align:center;}.css-4okk7a .katex .accent>.vlist-t{text-align:center;}.css-4okk7a .katex .accent .accent-body{position:relative;}.css-4okk7a .katex .accent .accent-body:not(.accent-full){width:0;}.css-4okk7a .katex .overlay{display:block;}.css-4okk7a .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-4okk7a .katex .mtable .arraycolsep{display:inline-block;}.css-4okk7a .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-4okk7a .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-4okk7a .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-4okk7a .katex .svg-align{text-align:left;}.css-4okk7a .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-4okk7a .katex svg path{stroke:none;}.css-4okk7a .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-4okk7a .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-4okk7a .katex .stretchy::before,.css-4okk7a .katex .stretchy::after{content:'';}.css-4okk7a .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-4okk7a .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-4okk7a .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .x-arrow-pad{padding:0 0.5em;}.css-4okk7a .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-4okk7a .katex .x-arrow,.css-4okk7a .katex .mover,.css-4okk7a .katex .munder{text-align:center;}.css-4okk7a .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-4okk7a .katex .fbox,.css-4okk7a .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-4okk7a .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-4okk7a .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-4okk7a .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-4okk7a .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-4okk7a .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-4okk7a .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-4okk7a .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-4okk7a .katex .mtr-glue{width:50%;}.css-4okk7a .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-4okk7a .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-4okk7a .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-4okk7a .katex-display{display:block;margin:1em 0;text-align:center;}.css-4okk7a .katex-display>.katex{display:block;white-space:nowrap;}.css-4okk7a .katex-display>.katex>.katex-html{display:block;position:relative;}.css-4okk7a .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-4okk7a .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-4okk7a .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-4okk7a body{counter-reset:katexEqnNo mmlEqnNo;}.css-4okk7a table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-4okk7a .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-4okk7a .tableBlock thead,.css-4okk7a .tableBlock thead th{border-bottom:1px solid #333!important;}.css-4okk7a .tableBlock th,.css-4okk7a .tableBlock td{padding:10px;text-align:left;}.css-4okk7a .tableBlock th{font-weight:bold!important;}.css-4okk7a .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-4okk7a .tableBlock caption>p{margin:0;}.css-4okk7a .tableBlock th>p,.css-4okk7a .tableBlock td>p{margin:0;}.css-4okk7a .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-4okk7a .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-4okk7a .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-4okk7a .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-4okk7a .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-4okk7a .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-4okk7a .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-4okk7a .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-4okk7a .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-4okk7a .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-4okk7a .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-4okk7a .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-4okk7a .tableBlock [data-text-align='center']{text-align:center;}.css-4okk7a .tableBlock [data-text-align='left']{text-align:left;}.css-4okk7a .tableBlock [data-text-align='right']{text-align:right;}.css-4okk7a .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-4okk7a .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-4okk7a .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-4okk7a .tableBlock__font-size--xxsmall{font-size:10px;}.css-4okk7a .tableBlock__font-size--xsmall{font-size:12px;}.css-4okk7a .tableBlock__font-size--small{font-size:14px;}.css-4okk7a .tableBlock__font-size--large{font-size:18px;}.css-4okk7a .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--bordered td,.css-4okk7a .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--borderless tbody+tbody,.css-4okk7a .tableBlock__border--borderless td,.css-4okk7a .tableBlock__border--borderless th,.css-4okk7a .tableBlock__border--borderless tr,.css-4okk7a .tableBlock__border--borderless thead,.css-4okk7a .tableBlock__border--borderless thead th{border:0!important;}.css-4okk7a .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-4okk7a .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-4okk7a .tableBlock__table-compactl th,.css-4okk7a .tableBlock__table-compact td{padding:3px!important;}.css-4okk7a .tableBlock__full-size{width:100%;}.css-4okk7a .textBlock{margin-bottom:16px;}.css-4okk7a .textBlock__text-formatting--finePrint{font-size:12px;}.css-4okk7a .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-4okk7a .textBlock__text-infoBox p{margin:0;}.css-4okk7a .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-4okk7a .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-4okk7a .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-4okk7a .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-4okk7a .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-4okk7a .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-4okk7a .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-4okk7a .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-4okk7a.css-4okk7a{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-4okk7a.css-4okk7a:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-4okk7a .js-external-link-button.link-like,.css-4okk7a .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-4okk7a .js-external-link-button.link-like:hover,.css-4okk7a .js-external-link-anchor:hover,.css-4okk7a .js-external-link-button.link-like:active,.css-4okk7a .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-4okk7a .js-external-link-button.link-like:focus-visible,.css-4okk7a .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-4okk7a p,.css-4okk7a div{margin:0px;display:block;}.css-4okk7a pre{margin:0px;display:block;}.css-4okk7a pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-4okk7a pre:not(:first-child){padding-top:8px;}.css-4okk7a ul,.css-4okk7a ol{display:block margin:0px;padding-left:20px;}.css-4okk7a ul li,.css-4okk7a ol li{padding-top:8px;}.css-4okk7a ul ul,.css-4okk7a ol ul,.css-4okk7a ul ol,.css-4okk7a ol ol{padding-top:0px;}.css-4okk7a ul:not(:first-child),.css-4okk7a ol:not(:first-child){padding-top:4px;} Braking time

Deceleration

Braking time

Does not include the perception-reaction time!

3 Motion Along a Straight Line

3.4 motion with constant acceleration, learning objectives.

By the end of this section, you will be able to:

• Identify which equations of motion are to be used to solve for unknowns.
• Use appropriate equations of motion to solve a two-body pursuit problem.

You might guess that the greater the acceleration of, say, a car moving away from a stop sign, the greater the car’s displacement in a given time. But, we have not developed a specific equation that relates acceleration and displacement. In this section, we look at some convenient equations for kinematic relationships, starting from the definitions of displacement, velocity, and acceleration. We first investigate a single object in motion, called single-body motion. Then we investigate the motion of two objects, called two-body pursuit problems .

First, let us make some simplifications in notation. Taking the initial time to be zero, as if time is measured with a stopwatch, is a great simplification. Since elapsed time is [latex] \text{Δ}t={t}_{\text{f}}-{t}_{0} [/latex], taking [latex] {t}_{0}=0 [/latex] means that[latex] \text{Δ}t={t}_{\text{f}} [/latex], the final time on the stopwatch. When initial time is taken to be zero, we use the subscript 0 to denote initial values of position and velocity. That is, [latex] {x}_{0} [/latex] is the initial position and [latex] {v}_{0} [/latex] is the initial velocity . We put no subscripts on the final values. That is, t is the final time , x is the final position , and v is the final velocity . This gives a simpler expression for elapsed time, [latex] \text{Δ}t=t [/latex]. It also simplifies the expression for x displacement, which is now [latex] \text{Δ}x=x-{x}_{0} [/latex]. Also, it simplifies the expression for change in velocity, which is now [latex] \text{Δ}v=v-{v}_{0} [/latex]. To summarize, using the simplified notation, with the initial time taken to be zero,

where the subscript 0 denotes an initial value and the absence of a subscript denotes a final value in whatever motion is under consideration.

We now make the important assumption that acceleration is constant . This assumption allows us to avoid using calculus to find instantaneous acceleration. Since acceleration is constant, the average and instantaneous accelerations are equal—that is,

Thus, we can use the symbol a for acceleration at all times. Assuming acceleration to be constant does not seriously limit the situations we can study nor does it degrade the accuracy of our treatment. For one thing, acceleration is constant in a great number of situations. Furthermore, in many other situations we can describe motion accurately by assuming a constant acceleration equal to the average acceleration for that motion. Lastly, for motion during which acceleration changes drastically, such as a car accelerating to top speed and then braking to a stop, motion can be considered in separate parts, each of which has its own constant acceleration.

Displacement and Position from Velocity

To get our first two equations, we start with the definition of average velocity:

Substituting the simplified notation for [latex] \text{Δ}x [/latex] and [latex] \text{Δ}t [/latex] yields

Solving for x gives us

where the average velocity is

The equation [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] reflects the fact that when acceleration is constant, v is just the simple average of the initial and final velocities. (Figure) illustrates this concept graphically. In part (a) of the figure, acceleration is constant, with velocity increasing at a constant rate. The average velocity during the 1-h interval from 40 km/h to 80 km/h is 60 km/h:

In part (b), acceleration is not constant. During the 1-h interval, velocity is closer to 80 km/h than 40 km/h. Thus, the average velocity is greater than in part (a).

Figure 3.18 (a) Velocity-versus-time graph with constant acceleration showing the initial and final velocities [latex] {v}_{0}\,\text{and}\,v [/latex]. The average velocity is [latex] \frac{1}{2}({v}_{0}+v)=60\,\text{km}\text{/}\text{h} [/latex]. (b) Velocity-versus-time graph with an acceleration that changes with time. The average velocity is not given by [latex] \frac{1}{2}({v}_{0}+v) [/latex], but is greater than 60 km/h.

Solving for Final Velocity from Acceleration and Time

We can derive another useful equation by manipulating the definition of acceleration:

Substituting the simplified notation for [latex] \text{Δ}v [/latex] and [latex] \text{Δ}t [/latex] gives us

Solving for v yields

Calculating Final Velocity

An airplane lands with an initial velocity of 70.0 m/s and then decelerates at 1.50 m/s 2 for 40.0 s. What is its final velocity?

First, we identify the knowns: [latex] {v}_{0}=70\,\text{m/s,}\,a=-1.50{\,\text{m/s}}^{2},t=40\,\text{s} [/latex].

Second, we identify the unknown; in this case, it is final velocity [latex] {v}_{\text{f}} [/latex].

Last, we determine which equation to use. To do this we figure out which kinematic equation gives the unknown in terms of the knowns. We calculate the final velocity using (Figure) , [latex] v={v}_{0}+at [/latex].

Show Answer

[latex] v={v}_{0}+at=70.0\,\text{m/s}+(-1.50\,\text{m/}{\text{s}}^{2})(40.0 s)=10.0 m/s. [/latex] (Figure) is a sketch that shows the acceleration and velocity vectors.

Figure 3.19 The airplane lands with an initial velocity of 70.0 m/s and slows to a final velocity of 10.0 m/s before heading for the terminal. Note the acceleration is negative because its direction is opposite to its velocity, which is positive.

Significance

The final velocity is much less than the initial velocity, as desired when slowing down, but is still positive (see figure). With jet engines, reverse thrust can be maintained long enough to stop the plane and start moving it backward, which is indicated by a negative final velocity, but is not the case here.

In addition to being useful in problem solving, the equation [latex] v={v}_{0}+at [/latex] gives us insight into the relationships among velocity, acceleration, and time. We can see, for example, that

• Final velocity depends on how large the acceleration is and how long it lasts
• If the acceleration is zero, then the final velocity equals the initial velocity ( v = v 0 ), as expected (in other words, velocity is constant)
• If a is negative, then the final velocity is less than the initial velocity

All these observations fit our intuition. Note that it is always useful to examine basic equations in light of our intuition and experience to check that they do indeed describe nature accurately.

Solving for Final Position with Constant Acceleration

We can combine the previous equations to find a third equation that allows us to calculate the final position of an object experiencing constant acceleration. We start with

Adding [latex] {v}_{0} [/latex] to each side of this equation and dividing by 2 gives

Since [latex] \frac{{v}_{0}+v}{2}=\overset{\text{–}}{v} [/latex] for constant acceleration, we have

Now we substitute this expression for [latex] \overset{\text{–}}{v} [/latex] into the equation for displacement, [latex] x={x}_{0}+\overset{\text{–}}{v}t [/latex], yielding

Calculating Displacement of an Accelerating Object

Dragsters can achieve an average acceleration of 26.0 m/s 2 . Suppose a dragster accelerates from rest at this rate for 5.56 s (Figure) . How far does it travel in this time?

Figure 3.20 U.S. Army Top Fuel pilot Tony “The Sarge” Schumacher begins a race with a controlled burnout. (credit: Lt. Col. William Thurmond. Photo Courtesy of U.S. Army.)

First, let’s draw a sketch (Figure) . We are asked to find displacement, which is x if we take [latex] {x}_{0} [/latex] to be zero. (Think about [latex] {x}_{0} [/latex] as the starting line of a race. It can be anywhere, but we call it zero and measure all other positions relative to it.) We can use the equation [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2} [/latex] when we identify [latex] {v}_{0} [/latex], [latex] a [/latex], and t from the statement of the problem.

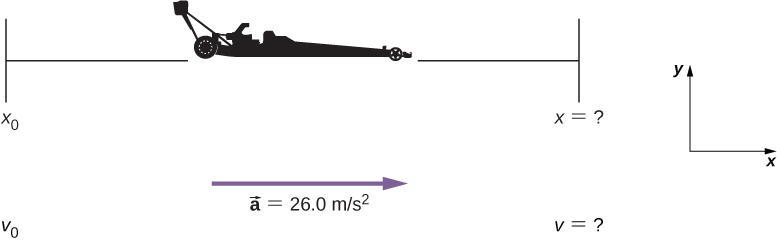
Figure 3.21 Sketch of an accelerating dragster.

Second, we substitute the known values into the equation to solve for the unknown:

[latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}. [/latex] Since the initial position and velocity are both zero, this equation simplifies to

[latex] x=\frac{1}{2}a{t}^{2}. [/latex] Substituting the identified values of a and t gives

[latex] x=\frac{1}{2}(26.0{\,\text{m/s}}^{2}){(5.56\,\text{s})}^{2}=402\,\text{m}\text{.} [/latex]

If we convert 402 m to miles, we find that the distance covered is very close to one-quarter of a mile, the standard distance for drag racing. So, our answer is reasonable. This is an impressive displacement to cover in only 5.56 s, but top-notch dragsters can do a quarter mile in even less time than this. If the dragster were given an initial velocity, this would add another term to the distance equation. If the same acceleration and time are used in the equation, the distance covered would be much greater.

What else can we learn by examining the equation [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}? [/latex] We can see the following relationships:

• Displacement depends on the square of the elapsed time when acceleration is not zero. In (Figure) , the dragster covers only one-fourth of the total distance in the first half of the elapsed time.
• If acceleration is zero, then initial velocity equals average velocity [latex] ({v}_{0}=\overset{\text{–}}{v}) [/latex], and [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}\,a{t}^{2}\,\text{becomes}\,x={x}_{0}+{v}_{0}t. [/latex]

Solving for Final Velocity from Distance and Acceleration

A fourth useful equation can be obtained from another algebraic manipulation of previous equations. If we solve [latex] v={v}_{0}+at [/latex] for t , we get

Substituting this and [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] into [latex] x={x}_{0}+\overset{\text{–}}{v}t [/latex], we get

Calculate the final velocity of the dragster in (Figure) without using information about time.

The equation [latex] {v}^{2}={v}_{0}^{2}+2a(x-{x}_{0}) [/latex] is ideally suited to this task because it relates velocities, acceleration, and displacement, and no time information is required.

BREAKSecond, we substitute the knowns into the equation [latex] {v}^{2}={v}_{0}^{2}+2a(x-{x}_{0}) [/latex] and solve for v:

BREAK[latex] {v}^{2}=0+2(26.0{\,\text{m/s}}^{2})(402\,\text{m}). [/latex] Thus, BREAK[latex] \begin{array}{ccc}{v}^{2}\hfill & =\hfill & 2.09\,×\,{10}^{4}\,{\text{m}}^{2}{\text{/s}}^{2}\hfill \\ \\ v\hfill & =\hfill & \sqrt{2.09\,×\,{10}^{4}{\,\text{m}}^{2}{\text{/s}}^{2}}=145\,\text{m/s}\text{.}\hfill \end{array} [/latex]

A velocity of 145 m/s is about 522 km/h, or about 324 mi/h, but even this breakneck speed is short of the record for the quarter mile. Also, note that a square root has two values; we took the positive value to indicate a velocity in the same direction as the acceleration.

An examination of the equation [latex] {v}^{2}={v}_{0}^{2}+2a(x-{x}_{0}) [/latex] can produce additional insights into the general relationships among physical quantities:

• The final velocity depends on how large the acceleration is and the distance over which it acts.
• For a fixed acceleration, a car that is going twice as fast doesn’t simply stop in twice the distance. It takes much farther to stop. (This is why we have reduced speed zones near schools.)

Putting Equations Together

In the following examples, we continue to explore one-dimensional motion, but in situations requiring slightly more algebraic manipulation. The examples also give insight into problem-solving techniques. The note that follows is provided for easy reference to the equations needed. Be aware that these equations are not independent. In many situations we have two unknowns and need two equations from the set to solve for the unknowns. We need as many equations as there are unknowns to solve a given situation.

Before we get into the examples, let’s look at some of the equations more closely to see the behavior of acceleration at extreme values. Rearranging (Figure) , we have

From this we see that, for a finite time, if the difference between the initial and final velocities is small, the acceleration is small, approaching zero in the limit that the initial and final velocities are equal. On the contrary, in the limit [latex] t\to 0 [/latex] for a finite difference between the initial and final velocities, acceleration becomes infinite.

Similarly, rearranging (Figure) , we can express acceleration in terms of velocities and displacement:

Thus, for a finite difference between the initial and final velocities acceleration becomes infinite in the limit the displacement approaches zero. Acceleration approaches zero in the limit the difference in initial and final velocities approaches zero for a finite displacement.

How Far Does a Car Go?

On dry concrete, a car can decelerate at a rate of 7.00 m/s 2 , whereas on wet concrete it can decelerate at only 5.00 m/s 2 . Find the distances necessary to stop a car moving at 30.0 m/s (about 110 km/h) on (a) dry concrete and (b) wet concrete. (c) Repeat both calculations and find the displacement from the point where the driver sees a traffic light turn red, taking into account his reaction time of 0.500 s to get his foot on the brake.

First, we need to draw a sketch (Figure) . To determine which equations are best to use, we need to list all the known values and identify exactly what we need to solve for.

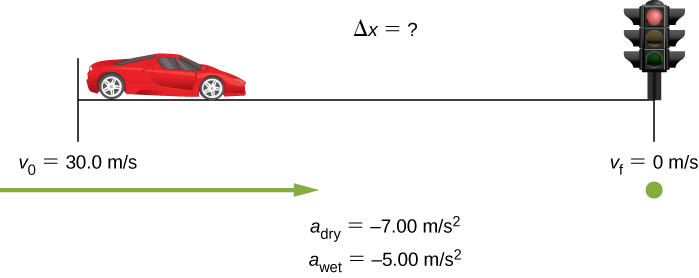
Figure 3.22 Sample sketch to visualize deceleration and stopping distance of a car.

This equation is best because it includes only one unknown, x . We know the values of all the other variables in this equation. (Other equations would allow us to solve for x , but they require us to know the stopping time, t , which we do not know. We could use them, but it would entail additional calculations.)

Third, we rearrange the equation to solve for x :

and substitute the known values:

• This part can be solved in exactly the same manner as (a). The only difference is that the acceleration is −5.00 m/s 2 . The result is [latex] {x}_{\text{wet}}=90.0\,\text{m on wet concrete.} [/latex]
• Show Answer When the driver reacts, the stopping distance is the same as it is in (a) and (b) for dry and wet concrete. So, to answer this question, we need to calculate how far the car travels during the reaction time, and then add that to the stopping time. It is reasonable to assume the velocity remains constant during the driver’s reaction time.To do this, we, again, identify the knowns and what we want to solve for. We know that [latex] \overset{\text{–}}{v}=30.0\,\text{m/s} [/latex], [latex] {t}_{\text{reaction}}=0.500\,\text{s} [/latex], and [latex] {a}_{\text{reaction}}=0 [/latex]. We take [latex] {x}_{\text{0-reaction}} [/latex] to be zero. We are looking for [latex] {x}_{\text{reaction}} [/latex].Second, as before, we identify the best equation to use. In this case, [latex] x={x}_{0}+\overset{\text{–}}{v}t [/latex] works well because the only unknown value is x, which is what we want to solve for.Third, we substitute the knowns to solve the equation: [latex] x=0+(30.0\,\text{m/s})(0.500\,\text{s})=15.0\,\text{m}. [/latex] This means the car travels 15.0 m while the driver reacts, making the total displacements in the two cases of dry and wet concrete 15.0 m greater than if he reacted instantly. Last, we then add the displacement during the reaction time to the displacement when braking ((Figure)), [latex] {x}_{\text{braking}}+{x}_{\text{reaction}}={x}_{\text{total}}, [/latex] and find (a) to be 64.3 m + 15.0 m = 79.3 m when dry and (b) to be 90.0 m + 15.0 m = 105 m when wet.

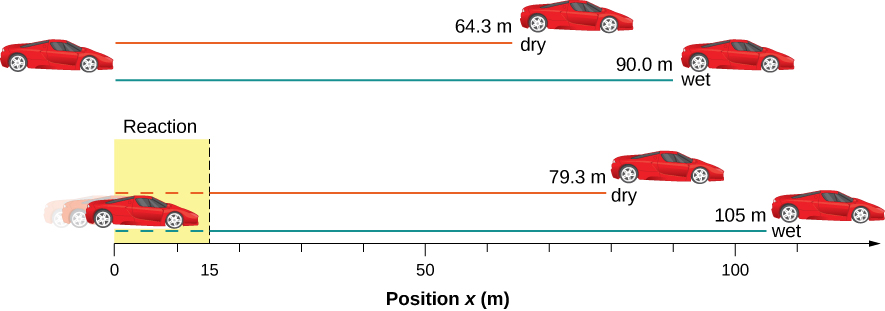
Figure 3.23 The distance necessary to stop a car varies greatly, depending on road conditions and driver reaction time. Shown here are the braking distances for dry and wet pavement, as calculated in this example, for a car traveling initially at 30.0 m/s. Also shown are the total distances traveled from the point when the driver first sees a light turn red, assuming a 0.500-s reaction time.

The displacements found in this example seem reasonable for stopping a fast-moving car. It should take longer to stop a car on wet pavement than dry. It is interesting that reaction time adds significantly to the displacements, but more important is the general approach to solving problems. We identify the knowns and the quantities to be determined, then find an appropriate equation. If there is more than one unknown, we need as many independent equations as there are unknowns to solve. There is often more than one way to solve a problem. The various parts of this example can, in fact, be solved by other methods, but the solutions presented here are the shortest.

Calculating Time

Suppose a car merges into freeway traffic on a 200-m-long ramp. If its initial velocity is 10.0 m/s and it accelerates at 2.00 m/s 2 , how long does it take the car to travel the 200 m up the ramp? (Such information might be useful to a traffic engineer.)

First, we draw a sketch (Figure) . We are asked to solve for time t . As before, we identify the known quantities to choose a convenient physical relationship (that is, an equation with one unknown, t .)

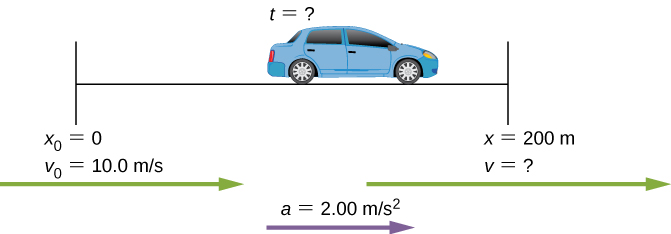
Figure 3.24 Sketch of a car accelerating on a freeway ramp.

[latex] {v}_{0}=10\,\text{m/s},a=2.00\,\text{m/}{\text{s}}^{2} [/latex], and x = 200 m.

We need to solve for t. The equation [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2} [/latex] works best because the only unknown in the equation is the variable t, for which we need to solve. From this insight we see that when we input the knowns into the equation, we end up with a quadratic equation.

We need to rearrange the equation to solve for t, then substituting the knowns into the equation:

[latex] 200\,\text{m}=0\,\text{m}+(10.0\,\text{m/s})t+\frac{1}{2}(2.00\,{\text{m/s}}^{2}){t}^{2}. [/latex]

We then simplify the equation. The units of meters cancel because they are in each term. We can get the units of seconds to cancel by taking t = t s, where t is the magnitude of time and s is the unit. Doing so leaves

[latex] 200=10t+{t}^{2}. [/latex] We then use the quadratic formula to solve for t,

[latex] \begin{array}{c}{t}^{2}+10t-200=0\\ \\ \\ t=\frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a},\end{array} [/latex] which yields two solutions: t = 10.0 and t = −20.0. A negative value for time is unreasonable, since it would mean the event happened 20 s before the motion began. We can discard that solution. Thus,

[latex] t=10.0\,\text{s}\text{.} [/latex]

Whenever an equation contains an unknown squared, there are two solutions. In some problems both solutions are meaningful; in others, only one solution is reasonable. The 10.0-s answer seems reasonable for a typical freeway on-ramp.

Check Your Understanding

A manned rocket accelerates at a rate of 20 m/s 2 during launch. How long does it take the rocket to reach a velocity of 400 m/s?

To answer this, choose an equation that allows us to solve for time t , given only a , v 0 , and v :

[latex] v={v}_{0}+at. [/latex]

Rearrange to solve for t :

[latex] t=\frac{v-{v}_{0}}{a}=\frac{400\,\text{m/s}-0\,\text{m/s}}{20{\,\text{m/s}}^{2}}=20\,\text{s}\text{.} [/latex]

Acceleration of a Spaceship

A spaceship has left Earth’s orbit and is on its way to the Moon. It accelerates at 20 m/s 2 for 2 min and covers a distance of 1000 km. What are the initial and final velocities of the spaceship?

We are asked to find the initial and final velocities of the spaceship. Looking at the kinematic equations, we see that one equation will not give the answer. We must use one kinematic equation to solve for one of the velocities and substitute it into another kinematic equation to get the second velocity. Thus, we solve two of the kinematic equations simultaneously.

[latex] x-{x}_{0}={v}_{0}t+\frac{1}{2}at [/latex] [latex] 1.0\,×\,{10}^{6}\,\text{m}={v}_{0}(120.0\,\text{s})+\frac{1}{2}(20.0{\text{m/s}}^{2}){(120.0\,\text{s})}^{2} [/latex] [latex] {v}_{0}=7133.3\,\text{m/s}\text{.} [/latex] Then we substitute [latex] {v}_{0} [/latex] into [latex] v={v}_{0}+at [/latex] to solve for the final velocity:

[latex] v={v}_{0}+at=7133.3\,\text{m/s}+(20.0\,{\text{m/s}}^{2})(120.0\,\text{s})=9533.3\,\text{m/s.} [/latex]

There are six variables in displacement, time, velocity, and acceleration that describe motion in one dimension. The initial conditions of a given problem can be many combinations of these variables. Because of this diversity, solutions may not be easy as simple substitutions into one of the equations. This example illustrates that solutions to kinematics may require solving two simultaneous kinematic equations.

With the basics of kinematics established, we can go on to many other interesting examples and applications. In the process of developing kinematics, we have also glimpsed a general approach to problem solving that produces both correct answers and insights into physical relationships. The next level of complexity in our kinematics problems involves the motion of two interrelated bodies, called two-body pursuit problems .

Two-Body Pursuit Problems

Up until this point we have looked at examples of motion involving a single body. Even for the problem with two cars and the stopping distances on wet and dry roads, we divided this problem into two separate problems to find the answers. In a two-body pursuit problem , the motions of the objects are coupled—meaning, the unknown we seek depends on the motion of both objects. To solve these problems we write the equations of motion for each object and then solve them simultaneously to find the unknown. This is illustrated in (Figure) .

Figure 3.25 A two-body pursuit scenario where car 2 has a constant velocity and car 1 is behind with a constant acceleration. Car 1 catches up with car 2 at a later time.

The time and distance required for car 1 to catch car 2 depends on the initial distance car 1 is from car 2 as well as the velocities of both cars and the acceleration of car 1. The kinematic equations describing the motion of both cars must be solved to find these unknowns.

Consider the following example.

Cheetah Catching a Gazelle

A cheetah waits in hiding behind a bush. The cheetah spots a gazelle running past at 10 m/s. At the instant the gazelle passes the cheetah, the cheetah accelerates from rest at 4 m/s 2 to catch the gazelle. (a) How long does it take the cheetah to catch the gazelle? (b) What is the displacement of the gazelle and cheetah?

We use the set of equations for constant acceleration to solve this problem. Since there are two objects in motion, we have separate equations of motion describing each animal. But what links the equations is a common parameter that has the same value for each animal. If we look at the problem closely, it is clear the common parameter to each animal is their position x at a later time t . Since they both start at [latex] {x}_{0}=0 [/latex], their displacements are the same at a later time t , when the cheetah catches up with the gazelle. If we pick the equation of motion that solves for the displacement for each animal, we can then set the equations equal to each other and solve for the unknown, which is time.

• Show Answer Equation for the gazelle: The gazelle has a constant velocity, which is its average velocity, since it is not accelerating. Therefore, we use (Figure) with [latex] {x}_{0}=0 [/latex]: [latex] x={x}_{0}+\overset{\text{–}}{v}t=\overset{\text{–}}{v}t. [/latex] Equation for the cheetah: The cheetah is accelerating from rest, so we use (Figure) with [latex] {x}_{0}=0 [/latex] and [latex] {v}_{0}=0 [/latex]: [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}=\frac{1}{2}a{t}^{2}. [/latex] Now we have an equation of motion for each animal with a common parameter, which can be eliminated to find the solution. In this case, we solve for t: [latex] \begin{array}{cc} x=\overset{\text{–}}{v}t=\frac{1}{2}a{t}^{2}\hfill \\ t=\frac{2\overset{\text{–}}{v}}{a}.\hfill \end{array} [/latex] The gazelle has a constant velocity of 10 m/s, which is its average velocity. The acceleration of the cheetah is 4 m/s2. Evaluating t, the time for the cheetah to reach the gazelle, we have [latex] t=\frac{2\overset{\text{–}}{v}}{a}=\frac{2(10)}{4}=5\,\text{s}\text{.} [/latex]
• Show Answer To get the displacement, we use either the equation of motion for the cheetah or the gazelle, since they should both give the same answer.Displacement of the cheetah: [latex] x=\frac{1}{2}a{t}^{2}=\frac{1}{2}(4){(5)}^{2}=50\,\text{m}\text{.} [/latex] Displacement of the gazelle: [latex] x=\overset{\text{–}}{v}t=10(5)=50\,\text{m}\text{.} [/latex] We see that both displacements are equal, as expected.

It is important to analyze the motion of each object and to use the appropriate kinematic equations to describe the individual motion. It is also important to have a good visual perspective of the two-body pursuit problem to see the common parameter that links the motion of both objects.

A bicycle has a constant velocity of 10 m/s. A person starts from rest and runs to catch up to the bicycle in 30 s. What is the acceleration of the person?

[latex] a=\frac{2}{3}{\,\text{m/s}}^{2} [/latex].

• When analyzing one-dimensional motion with constant acceleration, identify the known quantities and choose the appropriate equations to solve for the unknowns. Either one or two of the kinematic equations are needed to solve for the unknowns, depending on the known and unknown quantities.
• Two-body pursuit problems always require two equations to be solved simultaneously for the unknowns.

Conceptual Questions

When analyzing the motion of a single object, what is the required number of known physical variables that are needed to solve for the unknown quantities using the kinematic equations?

State two scenarios of the kinematics of single object where three known quantities require two kinematic equations to solve for the unknowns.

If the acceleration, time, and displacement are the knowns, and the initial and final velocities are the unknowns, then two kinematic equations must be solved simultaneously. Also if the final velocity, time, and displacement are the knowns then two kinematic equations must be solved for the initial velocity and acceleration.

A particle moves in a straight line at a constant velocity of 30 m/s. What is its displacement between t = 0 and t = 5.0 s?

A particle moves in a straight line with an initial velocity of 30 m/s and a constant acceleration of 30 m/s 2 . If at [latex] t=0,x=0 [/latex] and [latex] v=0 [/latex], what is the particle’s position at t = 5 s?

A particle moves in a straight line with an initial velocity of 30 m/s and constant acceleration 30 m/s 2 . (a) What is its displacement at t = 5 s? (b) What is its velocity at this same time?

b. [latex] v=180\,\text{m/s} [/latex]

(a) Sketch a graph of velocity versus time corresponding to the graph of displacement versus time given in the following figure. (b) Identify the time or times ( t a , t b , t c , etc.) at which the instantaneous velocity has the greatest positive value. (c) At which times is it zero? (d) At which times is it negative?

(a) Sketch a graph of acceleration versus time corresponding to the graph of velocity versus time given in the following figure. (b) Identify the time or times ( t a , t b , t c , etc.) at which the acceleration has the greatest positive value. (c) At which times is it zero? (d) At which times is it negative?

b. The acceleration has the greatest positive value at [latex] {t}_{a} [/latex]

c. The acceleration is zero at [latex] {t}_{e}\,\text{and}\,{t}_{h} [/latex]

d. The acceleration is negative at [latex] {t}_{i}\text{,}{t}_{j}\text{,}{t}_{k}\text{,}{t}_{l} [/latex]

A particle has a constant acceleration of 6.0 m/s 2 . (a) If its initial velocity is 2.0 m/s, at what time is its displacement 5.0 m? (b) What is its velocity at that time?

At t = 10 s, a particle is moving from left to right with a speed of 5.0 m/s. At t = 20 s, the particle is moving right to left with a speed of 8.0 m/s. Assuming the particle’s acceleration is constant, determine (a) its acceleration, (b) its initial velocity, and (c) the instant when its velocity is zero.

a. [latex] a=-1.3{\,\text{m/s}}^{2} [/latex];

b. [latex] {v}_{0}=18\,\text{m/s} [/latex];

c. [latex] t=13.8\,\text{s} [/latex]

A well-thrown ball is caught in a well-padded mitt. If the acceleration of the ball is[latex] 2.10\,×\,{10}^{4}{\,\text{m/s}}^{2} [/latex], and 1.85 ms [latex] (1\,\text{ms}={10}^{-3}\,\text{s}) [/latex] elapses from the time the ball first touches the mitt until it stops, what is the initial velocity of the ball?

A bullet in a gun is accelerated from the firing chamber to the end of the barrel at an average rate of [latex] 6.20\,×\,{10}^{5}{\,\text{m/s}}^{2} [/latex] for [latex] 8.10\,×\,{10}^{\text{−}4}\,\text{s} [/latex]. What is its muzzle velocity (that is, its final velocity)?

[latex] v=502.20\,\text{m/s} [/latex]

(a) A light-rail commuter train accelerates at a rate of 1.35 m/s 2 . How long does it take to reach its top speed of 80.0 km/h, starting from rest? (b) The same train ordinarily decelerates at a rate of 1.65 m/s 2 . How long does it take to come to a stop from its top speed? (c) In emergencies, the train can decelerate more rapidly, coming to rest from 80.0 km/h in 8.30 s. What is its emergency acceleration in meters per second squared?

While entering a freeway, a car accelerates from rest at a rate of 2.04 m/s 2 for 12.0 s. (a) Draw a sketch of the situation. (b) List the knowns in this problem. (c) How far does the car travel in those 12.0 s? To solve this part, first identify the unknown, then indicate how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, check your units, and discuss whether the answer is reasonable. (d) What is the car’s final velocity? Solve for this unknown in the same manner as in (c), showing all steps explicitly.

b. Knowns: [latex] a=2.40\,{\text{m/s}}^{2},t=12.0\,\text{s,}\,{v}_{0}=0\,\text{m/s} [/latex], and [latex] {x}_{0}=0\,\text{m} [/latex];

c. [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}=\frac{1}{2}a{t}^{2}=2.40\,\text{m/}{\text{s}}^{2}{(12.0\,\text{s})}^{2}=172.80\,\text{m} [/latex], the answer seems reasonable at about 172.8 m; d. [latex] v=28.8\,\text{m/s} [/latex]

Unreasonable results At the end of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of 2.00 m/s 2 . (a) How far does she travel in the next 5.00 s? (b) What is her final velocity? (c) Evaluate the result. Does it make sense?

Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart. (a) Make a sketch of the situation. (b) List the knowns in this problem. (c) How long does the acceleration take? To solve this part, first identify the unknown, then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units. (d) Is the answer reasonable when compared with the time for a heartbeat?

b. Knowns: [latex] v=30.0\,\text{cm}\text{/}\text{s,}\,x=1.80\,\text{cm} [/latex];

c. [latex] a=250\,\text{cm/}{\text{s}}^{2},\enspacet=0.12\,\text{s} [/latex];

During a slap shot, a hockey player accelerates the puck from a velocity of 8.00 m/s to 40.0 m/s in the same direction. If this shot takes [latex] 3.33\,×\,{10}^{\text{−}2}\,\text{s} [/latex], what is the distance over which the puck accelerates?

A powerful motorcycle can accelerate from rest to 26.8 m/s (100 km/h) in only 3.90 s. (a) What is its average acceleration? (b) How far does it travel in that time?

a. 6.87 s 2 ; b. [latex] x=52.26\,\text{m} [/latex]

Freight trains can produce only relatively small accelerations. (a) What is the final velocity of a freight train that accelerates at a rate of [latex] 0.0500\,{\text{m/s}}^{2} [/latex] for 8.00 min, starting with an initial velocity of 4.00 m/s? (b) If the train can slow down at a rate of [latex] 0.550\,{\text{m/s}}^{2} [/latex], how long will it take to come to a stop from this velocity? (c) How far will it travel in each case?

A fireworks shell is accelerated from rest to a velocity of 65.0 m/s over a distance of 0.250 m. (a) Calculate the acceleration. (b) How long did the acceleration last?

a. [latex] a=8450\,\text{m/}{\text{s}}^{2} [/latex];

b. [latex] t=0.0077\,\text{s} [/latex]

A swan on a lake gets airborne by flapping its wings and running on top of the water. (a) If the swan must reach a velocity of 6.00 m/s to take off and it accelerates from rest at an average rate of [latex] 0.35\,{\text{m/s}}^{2} [/latex], how far will it travel before becoming airborne? (b) How long does this take?

A woodpecker’s brain is specially protected from large accelerations by tendon-like attachments inside the skull. While pecking on a tree, the woodpecker’s head comes to a stop from an initial velocity of 0.600 m/s in a distance of only 2.00 mm. (a) Find the acceleration in meters per second squared and in multiples of g , where g = 9.80 m/s 2 . (b) Calculate the stopping time. (c) The tendons cradling the brain stretch, making its stopping distance 4.50 mm (greater than the head and, hence, less acceleration of the brain). What is the brain’s acceleration, expressed in multiples of g ?

a. [latex] a=9.18\,g; [/latex]

b. [latex] t=6.67\,×\,{10}^{-3}\,\text{s} [/latex];

c. [latex] \begin{array}{cc} a=\text{−}40.0\,{\text{m/s}}^{2}\hfill \\ a=4.08\,g\hfill \end{array} [/latex]

An unwary football player collides with a padded goalpost while running at a velocity of 7.50 m/s and comes to a full stop after compressing the padding and his body 0.350 m. (a) What is his acceleration? (b) How long does the collision last?

A care package is dropped out of a cargo plane and lands in the forest. If we assume the care package speed on impact is 54 m/s (123 mph), then what is its acceleration? Assume the trees and snow stops it over a distance of 3.0 m.

Knowns: [latex] x=3\,\text{m,}\,v=0\,\text{m/s,}\enspace{v}_{0}=54\,\text{m/s} [/latex]. We want a , so we can use this equation: [latex] a=\text{−}486\,{\text{m/s}}^{2} [/latex].

An express train passes through a station. It enters with an initial velocity of 22.0 m/s and decelerates at a rate of [latex] 0.150\,{\text{m/s}}^{2} [/latex] as it goes through. The station is 210.0 m long. (a) How fast is it going when the nose leaves the station? (b) How long is the nose of the train in the station? (c) If the train is 130 m long, what is the velocity of the end of the train as it leaves? (d) When does the end of the train leave the station?

Unreasonable results Dragsters can actually reach a top speed of 145.0 m/s in only 4.45 s. (a) Calculate the average acceleration for such a dragster. (b) Find the final velocity of this dragster starting from rest and accelerating at the rate found in (a) for 402.0 m (a quarter mile) without using any information on time. (c) Why is the final velocity greater than that used to find the average acceleration? ( Hint : Consider whether the assumption of constant acceleration is valid for a dragster. If not, discuss whether the acceleration would be greater at the beginning or end of the run and what effect that would have on the final velocity.)

a. [latex] a=32.58\,\text{m/}{\text{s}}^{2} [/latex];

b. [latex] v=161.85\,\text{m/s} [/latex];

c. [latex] v>{v}_{\text{max}} [/latex], because the assumption of constant acceleration is not valid for a dragster. A dragster changes gears and would have a greater acceleration in first gear than second gear than third gear, and so on. The acceleration would be greatest at the beginning, so it would not be accelerating at [latex] 32.6{\,\text{m/s}}^{2} [/latex] during the last few meters, but substantially less, and the final velocity would be less than [latex] 162\,\text{m/s} [/latex].

• OpenStax University Physics. Authored by : OpenStax CNX. Located at : https://cnx.org/contents/[email protected]:Gofkr9Oy@15 . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy