travelling salesman problem or

Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

2.1 Graph Theory
2.2 Classifications of the TSP
2.3 Variations of the TSP
3.1 aTSP ILP Formulation
3.2 sTSP ILP Formulation
4.1 Exact algorithms
4.2.1 Tour construction procedures
4.2.2 Tour improvement procedures
5 Applications
7 References

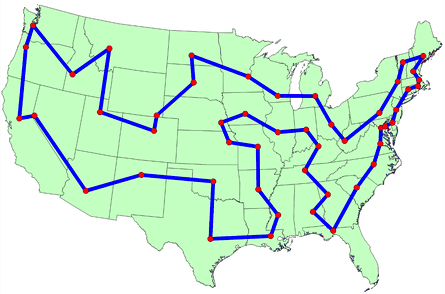
The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = (V, E)} be a directed or undirected graph with set of vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and set of edges Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \{(x,y) | x, y \in V\}} . 3,6 Each edge Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e \in E} is assigned a cost Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_e} . Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{H}} be the set of all Hamiltonian cycles, a cycle that visits each vertex exactly once, in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} . 6 The traveling salesman problem is to find the tour Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h \in \mathbb{H}} such that the sum of the costs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_e} in the tour is minimized.

Suppose graph Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is a complete graph, where every pair of distinct vertices is connected by a unique edge. 6 Let the set of vertices be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \{v_1, v_2, ..., v_n\}} . The cost matrix is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = (c_{ij})_{n \times n}} where the cost of the edge joining node Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_i} to node Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_j} , denoted Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ij}} , is given in entry Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i,j)} .

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is undirected
Applies when the distance between cities is the same in both directions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} is directed
Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation.

Given a set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} cities enumerated Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0, 1, ..., n-1} to be visited with the distance between each pair of cities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ij}} . 1 Introduce decision variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{ij}} for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i,j)} such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{ij} = \begin{cases} 1 ~~\text{if city }j\text{ is visited immediately after city }i\\ 0 ~~\text{otherwise} \end{cases} }

The objective function is then given by

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ \sum_i \sum_j c_{ij}y_{ij}\\ \text{s.t} & ~~ \sum_j y_{ij} = 1, ~~ i = 0, 1, ..., n-1 \\ & ~~ \sum_i y_{ij} = 1, ~~ j = 0, 1, ..., n-1 \\ & ~~ \sum_i \sum_j y_{ij} \le |S| - 1 ~~ S \subset V, 2 \le |S| \le n - 2 \\ & ~~ y_{ij} \in \{0,1\}, ~ \forall i,j \in E \\ \end{align} }

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ \sum_i \sum_j c_{ij}y_{ij}\\ \text{s.t} & ~~ \sum_{i < k} y_{ik} + \sum_{j > k} y_{kj} = 2, ~~ k \in V \\ & ~~ \sum_i \sum_j y_{ij} \le |S| - 1 ~~ S \subset V, 3 \le |S| \le n - 3 \\ & ~~ y_{ij} \in \{0,1\} ~ \forall i,j \in E \\ \end{align} }

Exact algorithms

The most direct solution algorithm is a complete enumeration of all possible path to determine the path of least cost. However, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} cities, the problem is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O(n!)} time, and this method is practical only for extremely small values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

Tour construction procedures where a solution is gradually built by adding a new vertex at each step
Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures, applications.

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

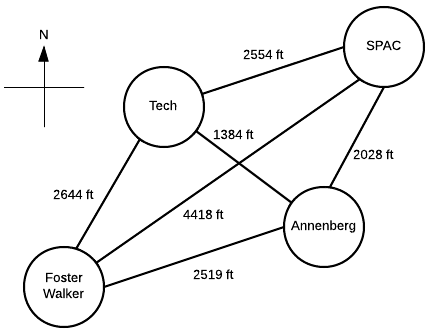
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

Drop off a homework set at Tech
Work out a SPAC
Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

Smallest distance is from Foster-Walker is to Annenberg
Smallest distance from Annenberg is to Tech
Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
Next smallest distance from Tech is to SPAC
Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

Smallest distance is Annenberg → Tech
Next smallest is SPAC → Annenberg
Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
Next smallest is Tech → Foster-Walker
Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

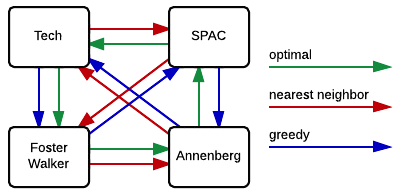
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
Goyal, S. (n.d.). A suvey on travlling salesman problem.
Pages with math errors
Pages with math render errors

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

The number of rows of the distance matrix, which is the number of locations (including the depot).
The number of vehicles in the problem.
The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices, from_index and to_index , and returns the corresponding entry of the distance matrix.

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples, dsa the traveling salesman problem.

The Traveling Salesman Problem

The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns.

Rules : Visit every city only once, then return back to the city you started in.

Goal : Find the shortest possible route.

Except for the Held-Karp algorithm (which is quite advanced and time consuming, ($O(2^n n^2)$), and will not be described here), there is no other way to find the shortest route than to check all possible routes.

This means that the time complexity for solving this problem is $O(n!)$, which means 720 routes needs to be checked for 6 cities, 40,320 routes must be checked for 8 cities, and if you have 10 cities to visit, more than 3.6 million routes must be checked!

Note: "!", or "factorial", is a mathematical operation used in combinatorics to find out how many possible ways something can be done. If there are 4 cities, each city is connected to every other city, and we must visit every city exactly once, there are $4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24$ different routes we can take to visit those cities.

The Traveling Salesman Problem (TSP) is a problem that is interesting to study because it is very practical, but so time consuming to solve, that it becomes nearly impossible to find the shortest route, even in a graph with just 20-30 vertices.

If we had an effective algorithm for solving The Traveling Salesman Problem, the consequences would be very big in many sectors, like for example chip design, vehicle routing, telecommunications, and urban planning.

Checking All Routes to Solve The Traveling Salesman Problem

To find the optimal solution to The Traveling Salesman Problem, we will check all possible routes, and every time we find a shorter route, we will store it, so that in the end we will have the shortest route.

Good: Finds the overall shortest route.

Bad: Requires an awful lot of calculation, especially for a large amount of cities, which means it is very time consuming.

How it works:

Check the length of every possible route, one route at a time.
Is the current route shorter than the shortest route found so far? If so, store the new shortest route.
After checking all routes, the stored route is the shortest one.

Such a way of finding the solution to a problem is called brute force .

Brute force is not really an algorithm, it just means finding the solution by checking all possibilities, usually because of a lack of a better way to do it.

Speed: {{ inpVal }}

Finding the shortest route in The Traveling Salesman Problem by checking all routes (brute force).

Progress: {{progress}}%

n = {{vertices}} cities

{{vertices}}!={{posRoutes}} possible routes

Show every route: {{showCompares}}

The reason why the brute force approach of finding the shortest route (as shown above) is so time consuming is that we are checking all routes, and the number of possible routes increases really fast when the number of cities increases.

Finding the optimal solution to the Traveling Salesman Problem by checking all possible routes (brute force):

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Since checking every possible route to solve the Traveling Salesman Problem (like we did above) is so incredibly time consuming, we can instead find a short route by just going to the nearest unvisited city in each step, which is much faster.

Good: Finds a solution to the Traveling Salesman Problem much faster than by checking all routes.

Bad: Does not find the overall shortest route, it just finds a route that is much shorter than an average random route.

Visit every city.
The next city to visit is always the nearest of the unvisited cities from the city you are currently in.
After visiting all cities, go back to the city you started in.

This way of finding an approximation to the shortest route in the Traveling Salesman Problem, by just going to the nearest unvisited city in each step, is called a greedy algorithm .

Finding an approximation to the shortest route in The Traveling Salesman Problem by always going to the nearest unvisited neighbor (greedy algorithm).

As you can see by running this simulation a few times, the routes that are found are not completely unreasonable. Except for a few times when the lines cross perhaps, especially towards the end of the algorithm, the resulting route is a lot shorter than we would get by choosing the next city at random.

Finding a near-optimal solution to the Traveling Salesman Problem using the nearest-neighbor algorithm (greedy):

Time Complexity for Solving The Traveling Salesman Problem

To get a near-optimal solution fast, we can use a greedy algorithm that just goes to the nearest unvisited city in each step, like in the second simulation on this page.

Solving The Traveling Salesman Problem in a greedy way like that, means that at each step, the distances from the current city to all other unvisited cities are compared, and that gives us a time complexity of $O(n^2) $.

But finding the shortest route of them all requires a lot more operations, and the time complexity for that is $O(n!)$, like mentioned earlier, which means that for 4 cities, there are 4! possible routes, which is the same as $4 \cdot 3 \cdot 2 \cdot 1 = 24$. And for just 12 cities for example, there are $12! = 12 \cdot 11 \cdot 10 \cdot \; ... \; \cdot 2 \cdot 1 = 479,001,600$ possible routes!

See the time complexity for the greedy algorithm $O(n^2)$, versus the time complexity for finding the shortest route by comparing all routes $O(n!)$, in the image below.

Time complexity for checking all routes versus running a greedy algorithm and finding a near-optimal solution instead.

But there are two things we can do to reduce the number of routes we need to check.

In the Traveling Salesman Problem, the route starts and ends in the same place, which makes a cycle. This means that the length of the shortest route will be the same no matter which city we start in. That is why we have chosen a fixed city to start in for the simulation above, and that reduces the number of possible routes from $n!$ to $(n-1)!$.

Also, because these routes go in cycles, a route has the same distance if we go in one direction or the other, so we actually just need to check the distance of half of the routes, because the other half will just be the same routes in the opposite direction, so the number of routes we need to check is actually $ \frac{(n-1)!}{2}$.

But even if we can reduce the number of routes we need to check to $ \frac{(n-1)!}{2}$, the time complexity is still $ O(n!)$, because for very big $n$, reducing $n$ by one and dividing by 2 does not make a significant change in how the time complexity grows when $n$ is increased.

To better understand how time complexity works, go to this page .

Actual Traveling Salesman Problems Are More Complex

The edge weight in a graph in this context of The Traveling Salesman Problem tells us how hard it is to go from one point to another, and it is the total edge weight of a route we want to minimize.

So far on this page, the edge weight has been the distance in a straight line between two points. And that makes it much easier to explain the Traveling Salesman Problem, and to display it.

But in the real world there are many other things that affects the edge weight:

Obstacles: When moving from one place to another, we normally try to avoid obstacles like trees, rivers, houses for example. This means it is longer and takes more time to go from A to B, and the edge weight value needs to be increased to factor that in, because it is not a straight line anymore.
Transportation Networks: We usually follow a road or use public transport systems when traveling, and that also affects how hard it is to go (or send a package) from one place to another.
Traffic Conditions: Travel congestion also affects the travel time, so that should also be reflected in the edge weight value.
Legal and Political Boundaries: Crossing border for example, might make one route harder to choose than another, which means the shortest straight line route might be slower, or more costly.
Economic Factors: Using fuel, using the time of employees, maintaining vehicles, all these things cost money and should also be factored into the edge weights.

As you can see, just using the straight line distances as the edge weights, might be too simple compared to the real problem. And solving the Traveling Salesman Problem for such a simplified problem model would probably give us a solution that is not optimal in a practical sense.

It is not easy to visualize a Traveling Salesman Problem when the edge length is not just the straight line distance between two points anymore, but the computer handles that very well.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with $n$ cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are $4!$, or 24, paths. However, if the size of this map is increased to 20 cities, there will be $1.22 \cdot 10^{17}$ paths!

The greedy approach to TSP would go like this:

Find all possible paths.
Find the cost of every paths.
Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of $O(n!)$. However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at $O(n^2 2^n)$. Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a $3/2$ approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then $P = NP$. As it stands, most scientists believe that $P \ne NP$.

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Travelling salesman problem

The travelling salesman problem (often abbreviated to TSP) is a classic problem in graph theory . It has many applications, in many fields. It also has quite a few different solutions.

The problem

The problem is usually stated in terms of a salesman who needs to visit several towns before eventually returning to the starting point. There are various routes he could take, visiting the different towns in different orders. Here is an example:

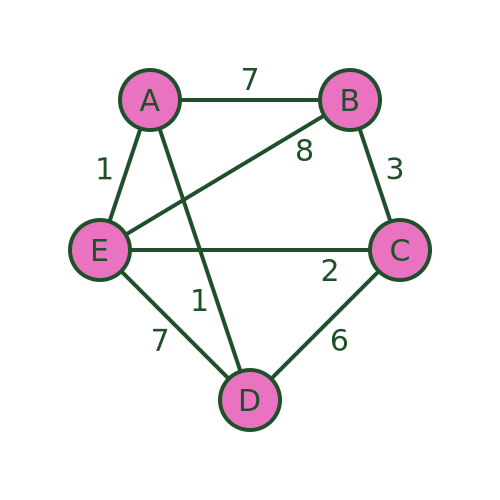
There are several different routes that will visit every town. For example, we could visit the towns in the order A , B , C , D , E , then back to A . Or we could use the route A , D , C , E , B then back to A .

But not all routes are possible. For example, we cannot use a route A , D , E , B , C and then back to A , because there is no road from C to A .

The aim is to find the route that visits all the towns with the minimum cost . The cost is shown as the weight of each edge in the graph. This might be the distance between the towns, or it might be some other measure. For example, it might be the time taken to travel between the towns, which might not be proportionate to the distance because some roads have lower speed limits or are more congested. Or, if the salesman was travelling by train, it might be the price of the tickets.

The salesman can decide to optimise for whatever measure he considers to be most important.

Alternative applications and variants

TSP applies to any problem that involves visiting various places in sequence. One example is a warehouse, where various items need to be fetched from different parts of a warehouse to collect the items for an order. In the simplest case, where one person fetches all the items for a single order and then packs and dispatches the items, a TSP algorithm can be used. Of course, a different route would be required for each order, which would be generated by the ordering system.

Another interesting example is printed circuit board (PCB) drilling. A PCB is the circuit board you will find inside any computer or other electronic device. They often need holes drilled in them, including mounting holes where the board is attached to the case and holes where component wires need to pass through the board. These holes are usually drilled by a robot drill that moves across the board to drill each hole in the correct place. TSP can be used to calculate the optimum drilling order.

The TSP algorithm can be applied to directed graphs (where the distance from A to B might be different to the distance from B to A ). Directed graphs can represent things like one-way streets (where the distance might not be the same in both directions) or flight costs (where the price of a single airline ticket might not be the same in both directions).

There are some variants of the TSP scenario. The mTSP problem covers the situation where there are several salesmen and exactly one salesman must visit each city. This applies to delivery vans, where there might be several delivery vans. The problem is to decide which parcels to place on each van and also to decide the route of each van.

The travelling purchaser problem is another variant. In that case, a purchaser needs to buy several items that are being sold in different places, potentially at different prices. The task is to purchase all the items, minimising the total cost (the cost of the items and the cost of travel). A simple approach would be to buy each item from the place where it is cheapest, in which case this becomes a simple TSP. However, it is not always worth buying every item from the cheapest place because sometimes the travel cost might outweigh the price difference.

In this article, we will only look at the basic TSP case.

Brute force algorithm

We will look at 3 potential algorithms here. There are many others. The first, and simplest, is the brute force approach.

We will assume that we start at vertex A . Since we intend to make a tour of the vertices (ie visit every vertex once and return to the original vertex) it doesn't matter which vertex we start at, the shortest loop will still be the same.

So we will start at A , visit nodes B , C , D , and E in some particular order, then return to A .

To find the shortest route, we will try every possible ordering of vertices B , C , D , E , and record the cost of each one. Then we can find the shortest.

For example, the ordering ABCDEA has a total cost of 7+3+6+7+1 = 24.

The ordering ABCEDA (i.e. swapping D and E ) has a total cost of 7+3+2+7+1 = 20.

Some routes, such as ADEBCA are impossible because a required road doesn't exist. We can just ignore those routes.

After evaluating every possible route, we are certain to find the shortest route (or routes, as several different routes may happen to have the same length that also happens to be the shortest length). In this case, the shortest route is AECBDA with a total length of 1+8+3+6+1 = 19.

The main problem with this algorithm is that it is very inefficient. In this example, since we have already decided that A is the start/end point, we must work out the visiting order for the 4 towns BCDE . We have 4 choices of the first town, 3 choices for the second town, 2 choices for the third town, and 1 choice for the fourth town. So there are 4! (factorial) combinations. That is only 24 combinations, which is no problem, you could even do it by hand.

If we had 10 towns (in addition to the home town) there would be 10! combinations, which is 3628800. Far too many to do by hand, but a modern PC might be able to do that in a fraction of a second if the algorithm was implemented efficiently.

If we had 20 towns, then the number of combinations would be of order 10 to the power 18. If we assume a computer that could evaluate a billion routes per second (which a typical PC would struggle to do, at least at the time of writing), that would take a billion seconds, which is several decades.

Of course, there are more powerful computers available, and maybe quantum computing will come into play soon, but that is only 20 towns. If we had 100 towns, the number of combinations would be around 10 to the power 157, and 1000 towns 10 to the power 2568. For some applications, it would be quite normal to have hundreds of vertices. The brute force method is impractical for all but the most trivial scenarios.

Nearest neighbour algorithm

The nearest neighbour algorithm is what we might call a naive attempt to find a good route with very little computation. The algorithm is quite simple and obvious, and it might seem like a good idea to someone who hasn't put very much thought into it. You start by visiting whichever town is closest to the starting point. Then each time you want to visit the next town, you look at the map and pick the closest town to wherever you happen to be (of course, you will ignore any towns that you have visited already). What could possibly go wrong?

Starting at A , we visit the nearest town that we haven't visited yet. In this case D and E are both distance 1 from A . We will (completely arbitrarily) always prioritise the connections in alphabetical order. So we pick D .

As an aside, if we had picked E instead we would get a different result. It might be better, but it is just as likely to be worse, so there is no reason to chose one over the other.

From D , the closest town is C with a distance of 6 (we can't pick A because we have already been there).

From C the closest town is E with distance 2. From E we have to go to B because we have already visited every other town - that is a distance of 8. And from B we must return to A with a distance of 7.

The final path is ADCEBA and the total distance is 1+6+2+8+7 = 24.

The path isn't the best, but it isn't terrible. This algorithm will often find a reasonable path, particularly if there is a natural shortest path. However, it can sometimes go badly wrong.

The basic problem is that the algorithm doesn't take account of the big picture. It just blindly stumbles from one town to whichever next town is closest.

In particular, the algorithm implicitly decides that the final step will be B to A . It does this based on the other distances, but without taking the distance BA into account. But what if, for example, there is a big lake between B and A that you have to drive all the way around? This might make the driving distance BA very large. A more sensible algorithm would avoid that road at all costs, but the nearest neighbour algorithm just blindly leads us there.

We can see this with this revised graph where BA has a distance of 50:

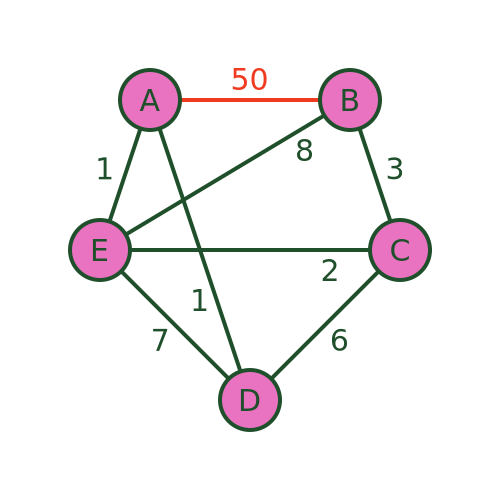
The algorithm will still recommend the same path because it never takes the distance BA into account. The path is still ADCEBA but the total distance is now 1+6+2+8+50 = 67. There are much better routes that avoid BA .

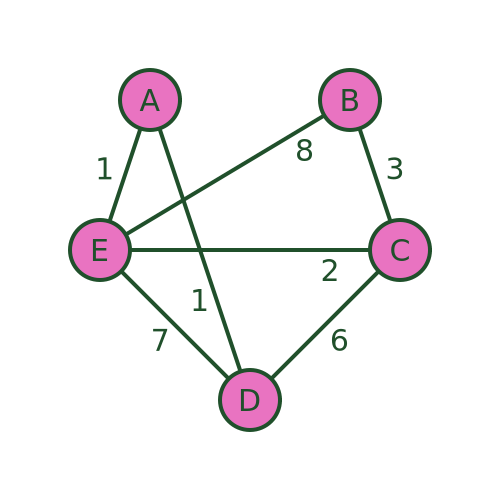
An even worse problem can occur if there is no road at all from B to A . The algorithm would still guide us to town B as the final visit. But in that case, it is impossible to get from B to A to complete the journey:

Bellman–Held–Karp algorithm

The Bellman–Held–Karp algorithm is a dynamic programming algorithm for solving TSP more efficiently than brute force. It is sometimes called the Held–Karp algorithm because it was discovered by Michael Held and Richard Karp, but it was also discovered independently by Richard Bellman at about the same time.

The algorithm assumes a complete graph (ie a graph where every vertex is connected to every other). However, it can be used with an incomplete graph like the one we have been using. To do this, we simply add extra the missing connections (shown below in grey) and assign them a very large distance (for example 1000). This ensures that the missing connections will never form part of the shortest path:

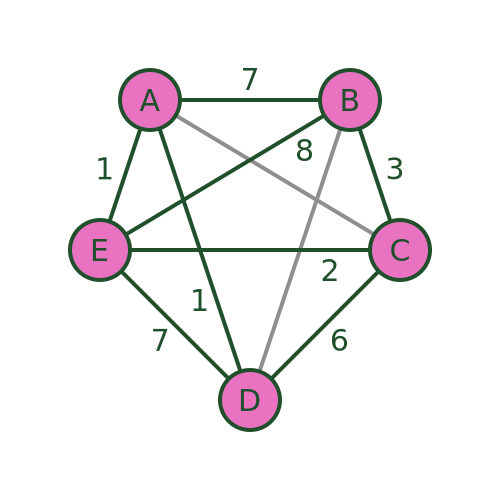
The technique works by incrementally calculating the shortest path for every possible set of 3 towns (starting from A ), then for every possible set of 4 towns, and so on until it eventually calculates the shortest path that goes from A via every other town and back to A .

Because the algorithm stores its intermediate calculations and discards non-optimal paths as early as possible, it is much more efficient than brute force.

We will use the following notation. We will use this to indicate the distance between towns A and B :

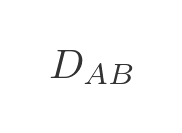
And we will use this to indicate the cost (ie the total distance) from A to C via B :

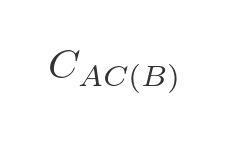
Here are some examples:

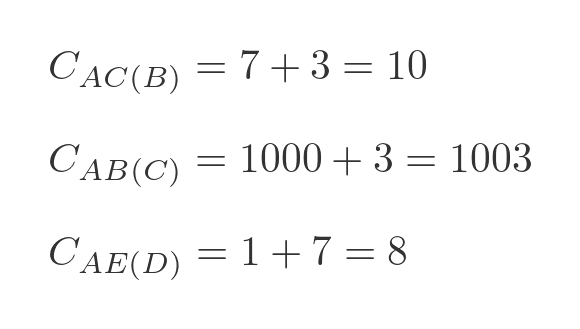
The first example is calculated by adding the distance AB to BC , which gives 10. The second example is calculated by adding AC to CB . But since there is no road from A to C , we give that a large dummy distance of 1000, so that total cost is 1003, which means it is never going to form a part of the shortest route. The third example is calculated by adding the distance AD to DE , which gives 8.

In the first step, we will calculate the value of every possible combination of 2 towns starting from A . There are 12 combinations: AB(C) , AB(D) , AB(E) , AC(B) , AC(D) , AC(E) , AD(B) , AD(C) , AD(E) , AE(B) , AE(C) , AE(D) .

These values will be stored for later use.

For step 2 we need to extend our notation slightly. We will use this to indicate the lowest cost from A to D via B and C (in either order):

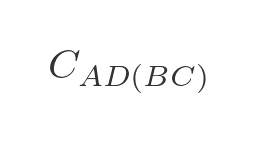
To be clear, this could represent one of two paths - ABCD or ACBD whichever is shorter. We can express this as a minimum of two values:

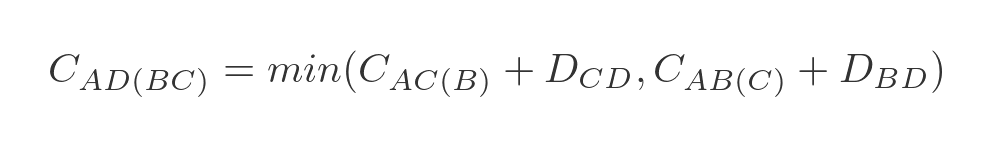
This represents the 2 ways to get from A to D via B and C :

We can travel from A to C via B , and then from C to D .
We can travel from A to B via C , and then from B to D .

We have already calculated A to C via B (and all the other combinations) in step 1, so all we need to do is add the values and find the smallest. In this case:

A to C via B is 10, C to D is 6, so the total is 16.
A to B via C is 1003, B to D is 1000, so the total is 2003.

Clearly, ABCD is the best route.

We need to repeat this for every possible combination of travelling from A to x via y and z . There are, again, 12 combinations: AB(CD) , AB(CE) , AB(DE) , AC(BD) , AC(BE) , AC(DE) , AD(BC) , AD(BE) , AD(CE) , AE(BC) , AE(BD) , AE(CD) .

We store these values, along with the optimal path, for later use.

In the next step, we calculate the optimal route for travelling from A to any other town via 3 intermediate towns. For example, travelling from A to E via B , C , and D (in the optimal order) is written as:

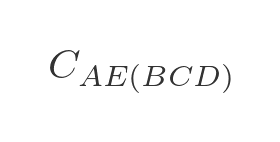
There are 3 paths to do this:

A to D via B and C , then from D to E .
A to C via B and D , then from C to E .
A to B via C and D , then from B to E .

We will choose the shortest of these three paths:

Again we have already calculated all the optimal intermediate paths. This time there are only 4 combinations we need to calculate: AB(CDE) , AC(BDE) , AD(BCE) , and AE(BCD) .

We are now in a position to calculate the optimal route for travelling from A back to A via all 4 other towns:

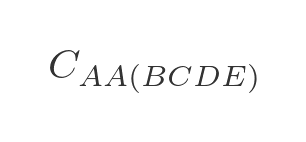
We need to evaluate each of the 4 options in step 3, adding on the extra distance to get back to A :

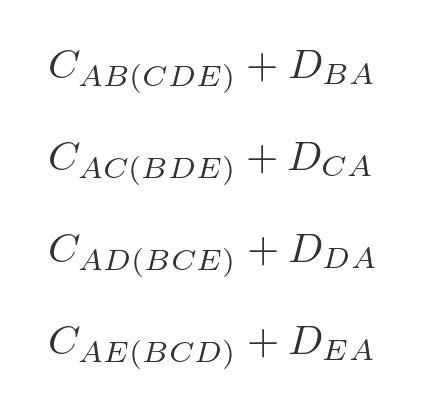
We can then choose the option that has the lowest total cost, and that will be the optimal route.

Performance

The performance of the Bellman–Held–Karp algorithm can be expressed in big-O notations as:

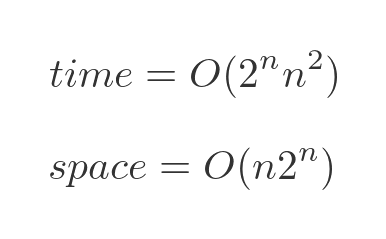
The time performance is approximately exponential. As the number of towns increases, the time taken will go up exponentially - each time an extra town is added, the time taken will double. We are ignoring the term in n squared because the exponential term is the most significant part.

Exponential growth is still quite bad, but it is far better than the factorial growth of the brute-force algorithm.

It is also important to notice that the algorithm requires memory to store the intermediate results, which also goes up approximately exponentially. The brute force algorithm doesn't have any significant memory requirements. However, that is usually an acceptable trade-off for a much better time performance.

The stages above describe how the algorithm works at a high level. We haven't gone into great detail about exactly how the algorithm keeps track of the various stages. Over the years since its discovery, a lot of work has been put into optimising the implementation. Optimising the implementation won't change the time complexity, which will still be roughly exponential. However, it might make the algorithm run several times faster than a poor implementation.

We won't cover this in detail, but if you ever need to use this algorithm for a serious purpose, it is worth considering using an existing, well-optimised implementation rather than trying to write it yourself. Unless you are just doing it for fun!

Other algorithms

Even the Bellman–Held–Karp algorithm has poor performance for modestly large numbers of towns. 100 towns, for example, would be well beyond the capabilities of a modern PC.

There are various heuristic algorithms that are capable of finding a good solution, but not necessarily the best possible solution, in a reasonable amount of time. I hope to cover these in a future article.

Adjacency matrices
The seven bridges of Königsberg
Permutation matrices and graphs
Dijkstra's algorithm

Join the GraphicMaths Newletter

Popular tags

adder adjacency matrix alu and gate angle area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle euler eulers formula exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irrational irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral radians radius rectangle regular polygon rhombus root set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume of revolution xnor gate xor gate

Graph theory
7 bridges of Königsberg
Binary numbers

$USA$

Traveling Salesman Problem

The Traveling Salesman Problem, or TSP for short, is one of the most intensively studied problems in computational mathematics. These pages are devoted to the history, applications, and current research of this challenge of finding the shortest route visiting each member of a collection of locations and returning to your starting point.

$travelling salesman problem or$

The work described here is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Department of Combinatorics and Optimization at the University of Waterloo .

12.9 Traveling Salesperson Problem

Learning objectives.

After completing this section, you should be able to:

Distinguish between brute force algorithms and greedy algorithms.
List all distinct Hamilton cycles of a complete graph.
Apply brute force method to solve traveling salesperson applications.
Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths . In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

Design of fiber optic networks
Minimizing fuel expenses for repositioning satellites
Development of semi-conductors for microchips
A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

An algorithm is a sequence of steps that can be used to solve a particular problem. We have solved many problems in this chapter, and the procedures that we used were different types of algorithms. In this section, we will use two common types of algorithms, a brute force algorithm and a greedy algorithm . A brute force algorithm begins by listing every possible solution and applying each one until the best solution is found. A greedy algorithm approaches a problem in stages, making the apparent best choice at each stage, then linking the choices together into an overall solution which may or may not be the best solution.

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.187 . Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

After phase 2, based on the information you have, you will choose the branch with 10, 7 and 4. Now, you are following a different branch than before, but it is the best choice based on the information you have. Let’s look at the last phase.

After phase 3, you will choose branch G which has a sum of 32.

The process of adding the values on each branch and selecting the highest sum is an example of a brute force algorithm because all options were explored in detail. The process of choosing the branch in phases, based on the best choice at each phase is a greedy algorithm. Although a brute force algorithm gives us the ideal solution, it can take a very long time to implement. Imagine a tree diagram with thousands or even millions of branches. It might not be possible to check all the sums. A greedy algorithm, on the other hand, can be completed in a relatively short time, and generally leads to good solutions, but not necessarily the ideal solution.

Example 12.42

Distinguishing between brute force and greedy algorithms.

A cashier rings up a sale for $4.63 cents in U.S. currency. The customer pays with a $5 bill. The cashier would like to give the customer $0.37 in change using the fewest coins possible. The coins that can be used are quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). The cashier starts by selecting the coin of highest value less than or equal to $0.37, which is a quarter. This leaves $ 0.37 − $ 0.25 = $ 0.12 $ 0.37 − $ 0.25 = $ 0.12 . The cashier selects the coin of highest value less than or equal to $0.12, which is a dime. This leaves $ 0.12 − $ 0.10 = $ 0.02 $ 0.12 − $ 0.10 = $ 0.02 . The cashier selects the coin of highest value less than or equal to $0.02, which is a penny. This leaves $ 0.02 − $ 0.01 = $ 0.01 $ 0.02 − $ 0.01 = $ 0.01 . The cashier selects the coin of highest value less than or equal to $0.01, which is a penny. This leaves no remainder. The cashier used one quarter, one dime, and two pennies, which is four coins. Use this information to answer the following questions.

Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Now let’s focus our attention on the graph theory application known as the traveling salesperson problem (TSP) in which we must find the shortest route to visit a number of locations and return to the starting point.

Recall from Hamilton Cycles , the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.192 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

Any route that visits each base and returns to the start would be a Hamilton cycle on the graph. If the officer wants to travel the shortest distance, this will correspond to a Hamilton cycle of lowest weight. We saw in Table 12.11 that there are six distinct Hamilton cycles (directed cycles) in a complete graph with four vertices, but some lie on the same cycle (undirected cycle) in the graph.

Since the distance between bases is the same in either direction, it does not matter if the officer travels clockwise or counterclockwise. So, there are really only three possible distances as shown in Figure 12.193 .

The possible distances are:

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

Notice that we listed all of the Hamilton cycles and found their weights when we solved the TSP about the officer from Vandenberg. This is a skill you will need to practice. To make sure you don't miss any, you can calculate the number of possible Hamilton cycles in a complete graph. It is also helpful to know that half of the directed cycles in a complete graph are the same cycle in reverse direction, so, you only have to calculate half the number of possible weights, and the rest are duplicates.

In a complete graph with n n vertices,

The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

TIP! When listing all the distinct Hamilton cycles in a complete graph, you can start them all at any vertex you choose. Remember, the cycle a → b → c → a is the same cycle as b → c → a → b so there is no need to list both.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
Which pairs of cycles must have the same weights? How do you know?
There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
Yes, they are all distinct cycles and there are 6 of them.
Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

TIP! When listing the possible cycles, ignore the vertex where the cycle begins and ends and focus on the ways to arrange the letters that represent the vertices in the middle. Using a systematic approach is best; for example, if you must arrange the letters M, O, and P, first list all those arrangements beginning with M, then beginning with O, and then beginning with P, as we did in Example 12.42.

Your Turn 12.43

The brute force method.

The method we have been using to find a Hamilton cycle of least weight in a complete graph is a brute force algorithm, so it is called the brute force method . The steps in the brute force method are:

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

On the next assignment, the air force officer must leave from Travis Air Force base, visit Beal, Edwards, and Vandenberg Air Force bases each exactly once and return to Travis Air Force base. There is no need to visit Los Angeles Air Force base. Use Figure 12.194 to find the shortest route.

Step 1: Since there are 4 vertices, there will be ( 4 − 1 ) ! = 3 ! = 6 ( 4 − 1 ) ! = 3 ! = 6 cycles, but half of them will be the reverse of the others; so, there will be ( 4 − 1 ) ! 2 = 6 2 = 3 ( 4 − 1 ) ! 2 = 6 2 = 3 possible distances.

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.195 .

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

The second path, T → B → V → E → T , and its reverse, T → E → V → B → T , have the least weight. The solution is that the officer should travel from Travis Air Force base to Beal Air Force Base, to Vandenberg Air Force base, to Edwards Air Force base, and return to Travis Air Force base, or the same route in reverse.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.194 . There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

When the brute force method is impractical for solving a traveling salesperson problem, an alternative is a greedy algorithm known as the nearest neighbor method , which always visit the closest or least costly place first. This method finds a Hamilton cycle of relatively low weight in a complete graph in which, at each phase, the next vertex is chosen by comparing the edges between the current vertex and the remaining vertices to find the lowest weight. Since the nearest neighbor method is a greedy algorithm, it usually doesn’t give the best solution, but it usually gives a solution that is "good enough." Most importantly, the number of steps will be the number of vertices. That’s right! A problem with 10 vertices requires 10 steps, not 362,880. Let’s look at an example to see how it works.

Suppose that a candidate for governor wants to hold rallies around the state. They plan to leave their home in city A , visit cities B, C, D, E , and F each once, and return home. The airfare between cities is indicated in the graph in Figure 12.196 .

Let’s help the candidate keep costs of travel down by applying the nearest neighbor method to find a Hamilton cycle that has a reasonably low weight. Begin by marking starting vertex as V 1 V 1 for "visited 1st." Then to compare the weights of the edges between A and vertices adjacent to A : $250, $210, $300, $200, and $100 as shown in Figure 12.197 . The lowest of these is $100, which is the edge between A and F .

Mark F as V 2 V 2 for "visited 2nd" then compare the weights of the edges between F and the remaining vertices adjacent to F : $170, $330, $150 and $350 as shown in Figure 12.198 . The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 V 3 for "visited 3rd." Next, compare the weights of the edges between D and the remaining vertices adjacent to D : $120, $310, and $270 as shown in Figure 12.199 . The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 V 4 for "visited 4th." Finally, compare the weights of the edges between B and the remaining vertices adjacent to B : $160 and $220 as shown in Figure 12.200 . The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 V 5 and mark the only remaining vertex, which is C , as V 6 V 6 . This is shown in Figure 12.201 . Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

The Hamilton cycle we found is A → F → D → B → E → C → A . The weight of the circuit is $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 $ 100 + $ 150 + $ 120 + $ 160 + $ 180 + $ 210 = $ 920 . This may or may not be the route with the lowest cost, but there is a good chance it is very close since the weights are most of the lowest weights on the graph and we found it in six steps instead of finding 120 different Hamilton cycles and calculating 60 weights. Let’s summarize the procedure that we used.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 2: Label the vertex at the end of the edge of lowest weight that you found in previous step as V n V n where the subscript n indicates the order the vertex is visited. Identify the edge of lowest weight between V n V n and the vertices that remain to be visited.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.202 . Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Step 3: A Hamilton cycle of low weight is A → D → F → C → B → E → A . So, a route of relatively low travel time is A to D to F to C to B to E and back to A . The total travel time of this route is: 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min 85 min + 70 min + 75 min + 100 min + 95 min + 90 min = 515 min or 8 hrs 35 min

Your Turn 12.45

Check your understanding, section 12.9 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

Authors: Donna Kirk
Publisher/website: OpenStax
Book title: Contemporary Mathematics
Publication date: Mar 22, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
Section URL: https://openstax.org/books/contemporary-mathematics/pages/12-9-traveling-salesperson-problem

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Data Structures
Linked List
Binary Tree
Binary Search Tree
Segment Tree
Disjoint Set Union
Fenwick Tree
Red-Black Tree
Advanced Data Structures
Dynamic Programming or DP
What is memoization? A Complete tutorial
Dynamic Programming (DP) Tutorial with Problems
Tabulation vs Memoization
Optimal Substructure Property in Dynamic Programming | DP-2
Overlapping Subproblems Property in Dynamic Programming | DP-1
Steps for how to solve a Dynamic Programming Problem

Advanced Topics

Bitmasking and Dynamic Programming | Set 1 (Count ways to assign unique cap to every person)
Digit DP | Introduction
Sum over Subsets | Dynamic Programming

Easy problems in Dynamic programming

Count all combinations of coins to make a given value sum (Coin Change II)
Subset Sum Problem
Introduction and Dynamic Programming solution to compute nCr%p
Cutting a Rod | DP-13
Painting Fence Algorithm
Longest Common Subsequence (LCS)
Longest Increasing Subsequence (LIS)
Longest subsequence such that difference between adjacents is one
Maximum size square sub-matrix with all 1s
Min Cost Path | DP-6
Longest Common Substring (Space optimized DP solution)
Count ways to reach the nth stair using step 1, 2 or 3
Count Unique Paths in matrix
Unique paths in a Grid with Obstacles

Medium problems on Dynamic programming

0/1 Knapsack Problem
Printing Items in 0/1 Knapsack
Unbounded Knapsack (Repetition of items allowed)
Egg Dropping Puzzle | DP-11
Word Break Problem | DP-32
Vertex Cover Problem (Dynamic Programming Solution for Tree)
Tile Stacking Problem
Box Stacking Problem | DP-22
Partition problem | DP-18

Travelling Salesman Problem using Dynamic Programming

Longest Palindromic Subsequence (LPS)
Longest Common Increasing Subsequence (LCS + LIS)
Find all distinct subset (or subsequence) sums of an array
Weighted Job Scheduling
Count Derangements (Permutation such that no element appears in its original position)
Minimum insertions to form a palindrome | DP-28
Ways to arrange Balls such that adjacent balls are of different types

Hard problems on Dynamic programming

Palindrome Partitioning
Word Wrap Problem
The Painter's Partition Problem
Program for Bridge and Torch problem
Matrix Chain Multiplication | DP-8
Printing brackets in Matrix Chain Multiplication Problem
Maximum sum rectangle in a 2D matrix | DP-27
Maximum profit by buying and selling a share at most k times
Minimum cost to sort strings using reversal operations of different costs
Count of AP (Arithmetic Progression) Subsequences in an array
Introduction to Dynamic Programming on Trees
Maximum height of Tree when any Node can be considered as Root
Longest repeating and non-overlapping substring
Top 20 Dynamic Programming Interview Questions

Travelling Salesman Problem (TSP):

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.

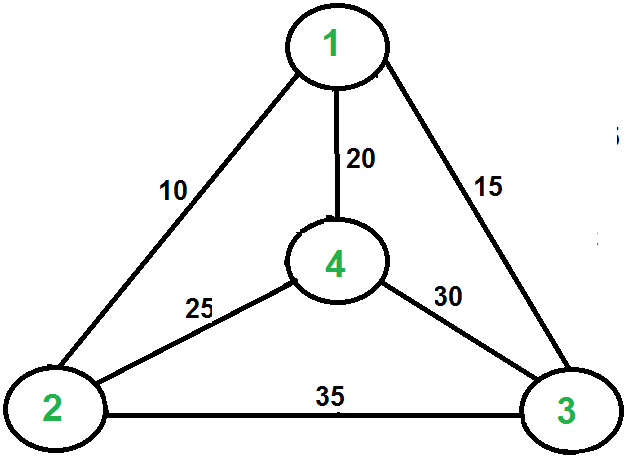
For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem.

Naive Solution:

1) Consider city 1 as the starting and ending point.

2) Generate all (n-1)! Permutations of cities.

3) Calculate the cost of every permutation and keep track of the minimum cost permutation.

4) Return the permutation with minimum cost.

Time Complexity: ?(n!)

Dynamic Programming:

Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex I (other than 1), we find the minimum cost path with 1 as the starting point, I as the ending point, and all vertices appearing exactly once. Let the cost of this path cost (i), and the cost of the corresponding Cycle would cost (i) + dist(i, 1) where dist(i, 1) is the distance from I to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far.

Now the question is how to get cost(i)? To calculate the cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems.

Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i . We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on. Note that 1 must be present in every subset.

Below is the dynamic programming solution for the problem using top down recursive+memoized approach:-

For maintaining the subsets we can use the bitmasks to represent the remaining nodes in our subset. Since bits are faster to operate and there are only few nodes in graph, bitmasks is better to use.

For example: –

10100 represents node 2 and node 4 are left in set to be processed

010010 represents node 1 and 4 are left in subset.

NOTE:- ignore the 0th bit since our graph is 1-based

Time Complexity : O(n 2 *2 n ) where O(n* 2 n) are maximum number of unique subproblems/states and O(n) for transition (through for loop as in code) in every states.

Auxiliary Space: O(n*2 n ), where n is number of Nodes/Cities here.

For a set of size n, we consider n-2 subsets each of size n-1 such that all subsets don’t have nth in them. Using the above recurrence relation, we can write a dynamic programming-based solution. There are at most O(n*2 n ) subproblems, and each one takes linear time to solve. The total running time is therefore O(n 2 *2 n ). The time complexity is much less than O(n!) but still exponential. The space required is also exponential. So this approach is also infeasible even for a slightly higher number of vertices. We will soon be discussing approximate algorithms for the traveling salesman problem.

Next Article: Traveling Salesman Problem | Set 2

References:

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Data Structures & Algorithms
DSA - Overview
DSA - Environment Setup
DSA - Algorithms Basics
DSA - Asymptotic Analysis
Data Structures
DSA - Data Structure Basics
DSA - Data Structures and Types
DSA - Array Data Structure
Linked Lists
DSA - Linked List Data Structure
DSA - Doubly Linked List Data Structure
DSA - Circular Linked List Data Structure
Stack & Queue
DSA - Stack Data Structure
DSA - Expression Parsing
DSA - Queue Data Structure
Searching Algorithms
DSA - Searching Algorithms
DSA - Linear Search Algorithm
DSA - Binary Search Algorithm
DSA - Interpolation Search
DSA - Jump Search Algorithm
DSA - Exponential Search
DSA - Fibonacci Search
DSA - Sublist Search
DSA - Hash Table
Sorting Algorithms
DSA - Sorting Algorithms
DSA - Bubble Sort Algorithm
DSA - Insertion Sort Algorithm
DSA - Selection Sort Algorithm
DSA - Merge Sort Algorithm
DSA - Shell Sort Algorithm
DSA - Heap Sort
DSA - Bucket Sort Algorithm
DSA - Counting Sort Algorithm
DSA - Radix Sort Algorithm
DSA - Quick Sort Algorithm
Graph Data Structure
DSA - Graph Data Structure
DSA - Depth First Traversal
DSA - Breadth First Traversal
DSA - Spanning Tree
Tree Data Structure
DSA - Tree Data Structure
DSA - Tree Traversal
DSA - Binary Search Tree
DSA - AVL Tree
DSA - Red Black Trees
DSA - B Trees
DSA - B+ Trees
DSA - Splay Trees
DSA - Tries
DSA - Heap Data Structure
DSA - Recursion Algorithms
DSA - Tower of Hanoi Using Recursion
DSA - Fibonacci Series Using Recursion
Divide and Conquer
DSA - Divide and Conquer
DSA - Max-Min Problem
DSA - Strassen's Matrix Multiplication
DSA - Karatsuba Algorithm
Greedy Algorithms
DSA - Greedy Algorithms
DSA - Travelling Salesman Problem (Greedy Approach)
DSA - Prim's Minimal Spanning Tree
DSA - Kruskal's Minimal Spanning Tree
DSA - Dijkstra's Shortest Path Algorithm
DSA - Map Colouring Algorithm
DSA - Fractional Knapsack Problem
DSA - Job Sequencing with Deadline
DSA - Optimal Merge Pattern Algorithm
Dynamic Programming
DSA - Dynamic Programming
DSA - Matrix Chain Multiplication
DSA - Floyd Warshall Algorithm
DSA - 0-1 Knapsack Problem
DSA - Longest Common Subsequence Algorithm
DSA - Travelling Salesman Problem (Dynamic Approach)
Approximation Algorithms
DSA - Approximation Algorithms
DSA - Vertex Cover Algorithm
DSA - Set Cover Problem
DSA - Travelling Salesman Problem (Approximation Approach)
Randomized Algorithms
DSA - Randomized Algorithms
DSA - Randomized Quick Sort Algorithm
DSA - Karger’s Minimum Cut Algorithm
DSA - Fisher-Yates Shuffle Algorithm
DSA Useful Resources
DSA - Questions and Answers
DSA - Quick Guide
DSA - Useful Resources
DSA - Discussion
Selected Reading
UPSC IAS Exams Notes
Developer's Best Practices
Questions and Answers
Effective Resume Writing
HR Interview Questions
Computer Glossary

Travelling Salesman Problem (Dynamic Approach)

Travelling salesman dynamic programming algorithm, implementation.

Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.

However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.

Let us consider a graph G = (V,E) , where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v) , which should be non-negative.

Suppose we have started at city 1 and after visiting some cities now we are in city j . Hence, this is a partial tour. We certainly need to know j , since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.

For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1 , and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j .

When |S|> 1 , we define 𝑪 C(S,1)= $\propto$ since the path cannot start and end at 1.

Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j . We should select the next city in such a way that

$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$

There are at the most 2 n .n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2 n .n 2 ) .

In the following example, we will illustrate the steps to solve the travelling salesman problem.

From the above graph, the following table is prepared.

$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$

$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$

$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$

$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$

$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$

$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$

$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$

$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$

$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$

$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$

The minimum cost path is 35.

Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.

When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Following are the implementations of the above approach in various programming languages −

To Continue Learning Please Login

The Traveling Salesman Problem

Optimization with the Attractor-Based Search System

School of Management, University of Michigan, Flint, USA

You can also search for this author in PubMed Google Scholar

Provides a complete understanding of the attractor concept in heuristic local searches
Presents a new search paradigm for solving a NP-complete combinatorial problem
Introduces the use of the attractor concept in dynamical systems theory to reduce the search space for TSP

Part of the book series: Synthesis Lectures on Operations Research and Applications (SLORA)

1180 Accesses

1 Citations

This is a preview of subscription content, log in via an institution to check access.

Access this book

Available as EPUB and PDF
Read on any device
Instant download
Own it forever
Durable hardcover edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Other ways to access

Licence this eBook for your library

Institutional subscriptions

Table of contents (8 chapters)

Front matter, introduction, traveling salesman problem, the attractor-based search system, analysis of the attractor-based search system, solving multi-objective traveling salesman problem, solving probabilistic traveling salesman problem, solving dynamic traveling salesman problem, solving dynamic multi-objective traveling salesman problem.

Combinatorial Optimization
Heuristic Local Search
Computing Theory and Algorithms
Operations Research
Global Optimization
Design and Analysis of Algorithms
P Versus NP Problem
Computational Complexity
Traveling Salesman Problem (TSP)
Dynamical Systems
NP-complete Combinatorial Problem

About this book

This book presents a new search paradigm for solving the Traveling Salesman Problem (TSP). The intrinsic difficulty of the TSP is associated with the combinatorial explosion of potential solutions in the solution space. The author introduces the idea of using the attractor concept in dynamical systems theory to reduce the search space for exhaustive search for the TSP. Numerous examples are used to describe how to use this new search algorithm to solve the TSP and its variants including: multi-objective TSP, dynamic TSP, and probabilistic TSP. This book is intended for readers in the field of optimization research and application.

Authors and Affiliations

About the author.

Weiqi Li, PhD, is an Associate Professor at the University of Michigan – Flint and an affiliated faculty in the Michigan Institute for Data Science at the University of Michigan. His research interests include combinatorial optimization, heuristics, supply chain management, and artificial intelligence. Specifically, Dr. Li’s research focuses on new search methods to solve the traveling salesman problem (TSP).

Bibliographic Information

Book Title : The Traveling Salesman Problem

Book Subtitle : Optimization with the Attractor-Based Search System

Authors : Weiqi Li

Series Title : Synthesis Lectures on Operations Research and Applications

DOI : https://doi.org/10.1007/978-3-031-35719-0

Publisher : Springer Cham

eBook Packages : Synthesis Collection of Technology (R0)

Copyright Information : The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG 2024

Hardcover ISBN : 978-3-031-35718-3 Published: 09 July 2023

Softcover ISBN : 978-3-031-35721-3 Due: 09 August 2023

eBook ISBN : 978-3-031-35719-0 Published: 08 July 2023

Series ISSN : 2770-6303

Series E-ISSN : 2770-6311

Edition Number : 1

Number of Pages : XIV, 141

Number of Illustrations : 58 b/w illustrations, 8 illustrations in colour

Topics : Operations Research, Management Science , Optimization , Applications of Mathematics , Complexity , Dynamical Systems and Ergodic Theory , Vibration, Dynamical Systems, Control

Publish with us

Policies and ethics

Find a journal
Track your research

What is a Travelling Salesman Problem (TSP)? Explained!

Author: Diksha Bhandari
Read Time: 9 min
Published: September 14, 2023
Last Update: November 8th, 2023

Table of Contents

TrackoField
What's New
Employee Management
Field Sales And Service
Task and Workflow
GPS Software
Lead Management
Fleet Management
Leave And Attendance
Video telematics
TrackoField Industries
Route Planning
Driver Behaviour
Last Mile Delivery
Asset Tracking
Dispatch Management
Fuel Management
Route Optimisation
Electric Vehicle
Roster Management
Vehicle Tracking
TrackoMile Industries
TrackoBit Industries
Sensor Integration
GPS Trackers and Hardware
Tech and Beyond

What is a Traveling Salesman Problem (TSP)

Want to know what a travelling salesman problem (TSP) is? Need solutions to real-life TSP challenges. Learn here.

Do you also look for the shortest route on Google Maps before embarking on a trip?

I am sure, you know multiple routes to reach the office, the mall, or your desired location, but checking on the internet before leaving home has become a ritual. It becomes all the more important to refer to maps when you have to pick up friends or colleagues along the way.

‘ADD STOPS’

Yes, you are right! 💯

That’s what solving the TSP challenge using software means!

What is a Travelling Salesman Problem (TSP)?

The traveling salesman problem is the popular combinatorial optimisation challenge in mathematics and computer science. The prime objective of the problem is to determine the shortest possible route a salesperson must take to cover a set of locations in one go and then return to the starting point.

Addressing travelling salesman challenges and their optimisation are more relevant in this time and age, especially in the supply chain, logistics and delivery space.

TSP may result in delayed deliveries and slimming profits as it’s not easy for delivery agents to choose the most viable and cost-effective route in real-time.

What are Traveling Salesman Problem Challenges to Solve?

When a salesperson is in the field hopping from one client site to another, finding out the best and the shortest route is an added pressure on the agent. In today’s day and age, distance isn’t the only factor that defines efficiency. There are several factors, such as time, fuel consumption, capacity, etc. that together define efficiency.

However, addressing the travelling salesman challenges involves mitigating a few unavoidable challenges along the way that field agents face themselves.

1. Time Constraints

Sales agents often have a tight schedule with multiple deliveries to make with a short TAT. Similarly, in TSP, optimising routes to minimise travel time is a fundamental challenge.

2. Last-minute Changes

Eleventh-hour changes are not a new concept for salespeople. They encounter urgent visits and last-minute cancellations a lot. Similarly, TSP solutions must be adaptable to handle dynamic scenarios and route modifications.

3. Resource Efficiency

Just as salespersons aim at reducing fuel costs and ensuring on-time deliveries, TSP solutions such as TrackoMile must strive for resource optimisation by reducing travel distances and delivery TAT.

4. Objective Diversification

While solving the travelling salesman problem (TSP) , optimising multiple objectives such as cost, time, and environmental factors adds complexity as solutions need to balance conflicting goals.

5. Combinatorial Complexity

TSP is a combinatorial optimisation problem, which means it involves complicated mathematical calculations with numerous variables. Sometimes, complex scenarios get further intricate as multiple variables are involved.

6. Adaptability and Scalability

Similarly, how sales agents adjust to the routes on the fly, the route algorithm must be flexible and responsive to real-time changes such as spiking volumes, vehicle breakdown or traffic slow down. A TSP solution must have a good appetite to handle large datasets and complex networks.

Also Read 4 Key Solutions for Fuel Management System 2023

1. Brute Force Algorithm

The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all. While it guarantees an optimal solution, its downside lies in its major time complexity, making it practical only for small TSP challenges.

2. Nearest Neighbour Algorithm

The Nearest Neighbour method is the simplest heuristic for the TSP. It starts from the first location and repeatedly selects the closest unvisited location to form a tour. Although it is quick to implement this method, it may always yield the optimal solution for it prioritises proximity over other factors.

Nearest neighbour Algorithm - Traveling Salesman Problem

3. Genetic Algorithm

This technique or method draws inspiration from nature itself. They evolve TSP solutions through selection, crossovers and mutation. They pick the best routes and mix them up. This creates new routes that might be even better. Then, they keep the best ones and repeat the mixing and picking process. Survival of the fittest in the true sense.

Genetic Algorithm - Traveling Salesman Problem

4. Ant Colony Optimisation (ACO)

Ants have a tendency to leave pheromones on the shorter routes they find, calling fellow ants on the same route. They keep leaving more pheromones on the shorter routes they find. Over time, the collective behaviour of the ants causes them to converge on the shortest route. Inspired by the nature of ants, ACO finds the shortest route by analysing the trails of data left by artificial ants based on the strength of these data trails.

Ant Colony Optimisation (ACO) - Traveling Salesman Problem

5. Dynamic Programming

Dynamic Programming is like solving a puzzle, step-by-step, by breaking it into smaller pieces. In TSP challenges, it finds the best route to visit all locations. It begins with figuring out the shortest route between two locations; then it builds on that to find ways to more locations. It’s a smart TSP solution for small scenarios but may require significant memory resources for larger and more complex problems.

What Are Real-world Travelling Salesman Problem Applications?

The Traveling Salesman Problem (TSP) has a wide array of applications across various domains due to its relevance in optimising routes and sequences. Here are several crucial real-word TSP applications and implementations in the real world.

1. TSP implementation in Logistics and Delivery Services

The logistics and supply chain sectors have the widest TSP applications.

Courier, Express & Parcel : Companies like FedEx, UPS, and DHL rely on TSP algorithms to optimise delivery routes for their fleet of delivery trucks. By finding the most efficient sequence of stops, they minimise fuel consumption , reduce delivery TAT, and save on operational overheads too.
On-demand Delivery : Food delivery companies, instant grocery delivery apps and at-home appointment platforms like Swiggy, BlinkIt and UrbanCompany, respectively, leverage TSP solutions to ensure timely delivery. Enhancing the customer experience and increasing the number of deliveries each rider can make.

2. TSP Applications in Transportation and Urban Planning Waste collection routes, Traffic light synchronisation, optic cable installation, etc. are some areas where TSP Solutions works like a knight in shining armour. Other real-world TSP applications include

Public Transport : City planners and public transport agencies use TSP principles to design bus, tram and train routes that reduce travel for passengers.
Emergency Service Dispatch : Ambulance services, Police PCR vans employ TSP algorithms to dispatch vehicles quickly and efficiently in response to emergency calls. Finding the shortest route to reach the incident location can save lives.
Urban Mobility Solution : In the era of ride-sharing and on-demand mobility apps like Uber, Ola, Lyft, etc., real-world TSP applications become prominent. TSP solutions optimise the route to destinations, ensuring quick and cost-effective transportation.

Other significant real-life applications of the Travelling Salesman Problem are

TSP in Healthcare and Medical Research – for DNA sequencing and understanding genetic patterns and diseases.
TSP in Manufacturing and Production – In circuit board manufacturing and job scheduling of technicians.
TSP in Robotics and Autonomous Vehicles -Self-driving cars and drones use TSP-like algorithms for efficient navigation.

Solving the Travelling Salesman Problem – Last Mile Delivery Route Optimisation

Route optimisation is the key to efficient last-mile delivery . In order to attain flawless route optimisation, the software must solve the traveling salesman problem every step of the way.

Why it’s essential to solve TSP for Last Mile Delivery?

In simple and minimal words, solving TSP problems helps in many ways:

Saves Time : It makes deliveries faster, so your customers get orders sooner.
Customer Satisfaction : Fast deliveries give you an edge over the competition and enhance customer experience too.
Saves Money : It reduces fuel wastage and vehicle wear, making deliveries cheaper.
Environment Friendly : It lowers pollution by using fewer vehicles and shorter routes.
Happy Staff: Drivers and dispatchers have less stress and can finish their work faster.

How do we solve the travelling salesman problem for last-mile delivery?

Solving TSP challenges for Last-mile delivery is like solving a big jigsaw puzzle. There are a hundred thousand addresses to visit daily. The software must find the shortest and most optimised route to them and come back to the starting point at the end.

Our route optimisation software , TrackoMile, leverages capacity management , routing algorithms and robust rule engines to present the most optimal combination of delivery addresses. Thereby giving the most optimally planned routes or trips.
All delivery managers have to do is upload the CSV file of the addresses or integrate TrackoMile to their CRM to fetch the delivery addresses. Now trip allocation, route optimisation, dispatch and everything else happen in a few clicks.
ETA when the delivery is en route, POD when the order is delivered successfully, and trip analysis, are added features to simplify overall operations.

The Vehicle Routing Problem is very similar to TSP, with wide applications in logistics, delivery services and transportation. While TSP focuses on finding the shortest route for a single traveller visiting various locations, VRP deals with multiple vehicles serving multiple customers, considering added constraints like vehicle capacity, TATs and more.

How Can AI Help in Solving Traveling Salesman Problem (TSP)?

AI or Artificial Intelligence are becoming the driving force for business growth across various industrial sectors. AI particularly aids in solving the Traveling Salesman Problem(TSP) in the logistics and delivery sector by employing advanced algorithms and techniques. What are a few tricks up AI’s sleeves that help in automating TSP resolution? Let’s find out!

1. Advanced Algorithms

AI algorithms such as Genetic Algorithms, ACO, simulated annealing and a few others mentioned above, tackle complex Travelling Salesman Problem scenarios.

2. Machine Learning

Gathering information from historical data and optimising routes based on real-time insights is what AI is best for. Machine learning models are trained to adapt to changing conditions, like traffic, weather and delivery constraints, to provide a more accurate plan of action.

3. Parallel Computing

AIi enables the use of a parallel computing process, which means solving multiple segments of TSP simultaneously. This accelerates the problem-solving process for large-scale challenges.

4. Heuristic Improvement

TSP Heuristics powered by AI can groom initial solutions, gradually improving their results over time. These heuristics can be applied iteratively by AI to reach better results.

5. Hybrid Approaches

Applying hybrid algorithms is not a new technique to refine techniques and produce more accurate results. AI on top of it singles out data-oriented combinations that work the best in varied use cases.

Wrapping Up!

The travelling salesman problem’s importance lies in its real-world applications. Whether optimising delivery routes, planning manufacturing processes or organising circuit board drilling, finding the most efficient way to cover multiple locations is crucial to minimise costs and save time.

The TSP problems have evolved over the years, and so have TSP algorithms, heuristics and solutions. With the advent of advanced technologies such as GPS and machine learning, TSP continues to adapt and find new applications in emerging fields, cementing its status as a fundamental problem in optimization theory and a valuable tool for various industries. Mobility automation software like Trackobit, TrackoMile and TrackoField resort to TSP heuristics to solve challenges along the way.

Read Blog – Best Delivery Route Planner Apps for 2023

Traveling Salesman Problem FAQs

What is tsp.

TSP is an abbreviation for Traveling Salesman Problem. It’s the routing problem that deals with finding the shortest route to travel to a combination of locations in the most optimal manner.

Is Travelling Salesman Problem Solvable?

Yes, the Traveling Salesman Problem (TSP) is solvable, but the time to find the solution can grow proportionately with an increase in the number of locations. With the evolution of travelling salesman problem applications, various TSP algorithms and heuristics, their hybrids have also emerged.

Wh at is the objective of TSP?

The objective of the Traveling Salesman Problem (TSP) is to find the shortest possible route that covers all given locations or waypoints and comes back to the starting point with the least resource utilisation.

Diksha Bhandari

Currently creating SaaSy content strategies for TrackoBit and TrackoField, this content professional has dedicated a decade of her life to enriching her portfolio and continues to do so. In addition to playing with words and spilling SaaS, she has a passion for traveling to the mountains and sipping on adrak wali chai.

Author Showcase
All Blog Post

Never Miss a Beat

Related Blog

Top 12 Google Map Alternatives – Offering Precise Navigation

Explore our best picks for 12 free Google map alternatives that offer accurate and secure location and navigational solutions.

Food Delivery Trends to Watch in 2024 & Beyond

Food and technology are both revolving along with consumer demands. Here are some of the food delivery trends to watch in 2024.

Biofuel – An Alternative to Fossil Fuels in Transportation | G20

Transportation industries are moving towards a greener future through the sustainable use of biofuels like Ethanol — discussed in the G20 2023 summit.

Top 10 Navigation Apps for Android and iOS | 2024

Discover the 10 best navigation apps in 2024 that offer personalised navigation just like Sherpas (experienced guides of Himalayan terrain) do.

Thank you for reaching out! We'll speak to you soon.

In the meantime, why not find out more about us, explore our products, or visit our blog?

Stay Updated on tech, telematics and mobility. Don't miss out on the latest in the industry.

Cookie Consent

We use cookies to enhance and personalize your browsing experience. By continuing to use our website, you agree to our Privacy Policy.

Subscribe to the PwC Newsletter

Join the community, edit social preview.

Add a new code entry for this paper

Remove a code repository from this paper, mark the official implementation from paper authors, add a new evaluation result row, remove a task, add a method, remove a method, edit datasets, a faster heuristic for the traveling salesman problem with drone.

28 May 2024 · Pedro H. D. B. Hokama , Carla N. Lintzmayer , Mário C. San Felice · Edit social preview

Given a set of customers, the Flying Sidekick Traveling Salesman Problem (FSTSP) consists of using one truck and one drone to perform deliveries to them. The drone is limited to delivering to one customer at a time, after which it returns to the truck, from where it can be launched again. The goal is to minimize the time required to service all customers and return both vehicles to the depot. In the literature, we can find heuristics for this problem that follow the order-first split-second approach: find a Hamiltonian cycle h with all customers, and then remove some customers to be handled by the drone while deciding from where the drone will be launched and where it will be retrieved. Indeed, they optimally solve the h-FSTSP, which is a variation that consists of solving the FSTSP while respecting a given initial cycle h. We present the Lazy Drone Property, which guarantees that only some combinations of nodes for launch and retrieval of the drone need to be considered by algorithms for the h-FSTSP. We also present an algorithm that uses the property, and we show experimental results which corroborate its effectiveness in decreasing the running time of such algorithms. Our algorithm was shown to be more than 84 times faster than the previously best-known ones over the literature benchmark. Moreover, on average, it considered a number of launch and retrieval pairs that is linear on the number of customers, indicating that the algorithm's performance should be sustainable for larger instances.

Code Edit Add Remove Mark official

Datasets edit.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

12.10: Traveling Salesperson Problem

Last updated
Save as PDF
Page ID 129677

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$Three doors are shown side-by-side.$

Learning Objectives

After completing this section, you should be able to:

Distinguish between brute force algorithms and greedy algorithms.
List all distinct Hamilton cycles of a complete graph.
Apply brute force method to solve traveling salesperson applications.
Apply nearest neighbor method to solve traveling salesperson applications.

We looked at Hamilton cycles and paths in the previous sections Hamilton Cycles and Hamilton Paths. In this section, we will analyze Hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. Besides the many routing applications in which we need the shortest distance, there are also applications in which we search for the route that is least expensive or takes the least time. Here are a few less common applications that you can read about on a website set up by the mathematics department at the University of Waterloo in Ontario, Canada:

Design of fiber optic networks
Minimizing fuel expenses for repositioning satellites
Development of semi-conductors for microchips
A technique for mapping mammalian chromosomes in genome sequencing

Before we look at approaches to solving applications like these, let's discuss the two types of algorithms we will use.

Brute Force and Greedy Algorithms

To understand the difference between these two algorithms, consider the tree diagram in Figure 12.214. Suppose we want to find the path from left to right with the largest total sum. For example, branch A in the tree diagram has a sum of 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36 .

$A graph has 15 vertices. The vertices are labeled 1 to 15. 10 branches into 2 and 7. 2 branches into 11 and 15. 11 branches into 13 and 8. 15 branches into 1 and 6. 7 branches into 3 and 4. 3 branches into 20 and 14. 4 branches into 11 and 5. 13, 8, 1, 6, 20, 14, 11, and 5 are labeled A to H.$

To be certain that you pick the branch with greatest sum, you could list each sum from each of the different branches:

A : 10 + 2 + 11 + 13 = 36 10 + 2 + 11 + 13 = 36

B : 10 + 2 + 11 + 8 = 31 10 + 2 + 11 + 8 = 31

C : 10 + 2 + 15 + 1 = 28 10 + 2 + 15 + 1 = 28

D : 10 + 2 + 15 + 6 = 33 10 + 2 + 15 + 6 = 33

E : 10 + 7 + 3 + 20 = 40 10 + 7 + 3 + 20 = 40

F : 10 + 7 + 3 + 14 = 34 10 + 7 + 3 + 14 = 34

G : 10 + 7 + 4 + 11 = 32 10 + 7 + 4 + 11 = 32

H : 10 + 7 + 4 + 5 = 26 10 + 7 + 4 + 5 = 26

Then we know with certainty that branch E has the greatest sum.

Now suppose that you wanted to find the branch with the highest value, but you only were shown the tree diagram in phases, one step at a time.

$A graph has 3 vertices. The vertices are labeled 10, 2, and 7. 10 branches into 2 and 7. The edge, 10 to 7 is highlighted.$

After phase 1, you would have chosen the branch with 10 and 7. So far, you are following the same branch. Let’s look at the next phase.

$A graph has 5 vertices. The vertices are labeled 10, 2, 7, 3, and 4. 10 branches into 2 and 7. 7 branches into 3 and 4. The edges, 10 to 7 and 7 to 4 are highlighted.$

$A graph has 7 vertices. The vertices are labeled 10, 2, 7, 3, 4, 11, and 15. 10 branches into 2 and 7. 7 branches into 3 and 4. 4 branches into 11 and 5. The edges, 10 to 7, 7 to 4, and 4 to 11 are highlighted. 11 and 5 are labeled G and H.$

After phase 3, you will choose branch G which has a sum of 32.

Example 12.42

Distinguishing between brute force and greedy algorithms.

Is the cashier’s approach an example of a greedy algorithm or a brute force algorithm? Explain how you know.
The cashier’s solution is the best solution. In other words, four is the fewest number of coins possible. Is this consistent with the results of an algorithm of this kind? Explain your reasoning.
The approach the cashier used is an example of a greedy algorithm, because the problem was approached in phases and the best choice was made at each phase. Also, it is not a brute force algorithm, because the cashier did not attempt to list out all possible combinations of coins to reach this conclusion.
Yes, it is consistent. A greedy algorithm does not always yield the best result, but sometimes it does.

Your Turn 12.42

The traveling salesperson problem.

Recall from Hamilton Cycles, the officer in the U.S. Air Force who is stationed at Vandenberg Air Force base and must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needed to visit each base once. We looked at the weighted graph in Figure 12.219 representing the four U.S. Air Force bases: Vandenberg, Edwards, Los Angeles, and Beal and the distances between them.

$A graph represents the four California air force bases. The graph has four vertices: E, B, V, and L. The edge, E B is labeld 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles.$

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines.$

a → b → c → d → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, ad, and bc are in dashed lines. Directed edges flow from a to b, b to d, d to c, and c to a.$

a → b → d → c → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and dc are in dashed lines. Directed edges flow from a to c, c to b, b to d, and d to a.$

a → c → b → d → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines. Directed edges flow from a to d, d to c, c to b, and b to a.$

a → d → c → b → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a d, and bc are in dashed lines. The directed edges flow from a to c, c to d, d to b, and b to a.$

a → c → d → b → a

$A graph has four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and dc are in dashed lines. The edges flow from a to d, d to b, b to c, and c to a.$

a → d → b → c → a

$Three graphs represent the four California air force bases. Each graph has four vertices: E, B, V, and L. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. In the first graph, the edges, E V, and L B are in dashed lines. In the second graph, the edges, E L and B V are in dashed lines. In the third graph, the edges, E B and L V are in dashed lines.$

The possible distances are:

396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148 396 + 410 + 106 + 159 = 1071 207 + 410 + 439 + 159 = 1215 396 + 439 + 106 + 207 = 1148

So, a Hamilton cycle of least weight is V → B → E → L → V (or the reverse direction). The officer should travel from Vandenberg to Beal to Edwards, to Los Angeles, and back to Vandenberg.

Finding Weights of All Hamilton Cycles in Complete Graphs

In a complete graph with n n vertices,

The number of distinct Hamilton cycles is ( n − 1 ) ! ( n − 1 ) ! .
There are at most ( n − 1 ) ! 2 ( n − 1 ) ! 2 different weights of Hamilton cycles.

Example 12.43

Calculating possible weights of hamilton cycles.

Suppose you have a complete weighted graph with vertices N, M, O , and P .

Use the formula ( n − 1 ) ! ( n − 1 ) ! to calculate the number of distinct Hamilton cycles in the graph.
Use the formula ( n − 1 ) ! 2 ( n − 1 ) ! 2 to calculate the greatest number of different weights possible for the Hamilton cycles.
Are all of the distinct Hamilton cycles listed here? How do you know? Cycle 1: N → M → O → P → N Cycle 2: N → M → P → O → N Cycle 3: N → O → M → P → N Cycle 4: N → O → P → M → N Cycle 5: N → P → M → O → N Cycle 6: N → P → O → M → N
Which pairs of cycles must have the same weights? How do you know?
There are 4 vertices; so, n = 4 n = 4 . This means there are ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ⋅ 2 ⋅ 1 = 6 distinct Hamilton cycles beginning at any given vertex.
Since n = 4 n = 4 , there are ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 ( n − 1 ) ! 2 = ( 4 − 1 ) ! 2 = 6 2 = 3 possible weights.
Yes, they are all distinct cycles and there are 6 of them.
Cycles 1 and 6 have the same weight, Cycles 2 and 4 have the same weight, and Cycles 3 and 5 have the same weight, because these pairs follow the same route through the graph but in reverse.

Your Turn 12.43

The brute force method.

Step 1: Calculate the number of distinct Hamilton cycles and the number of possible weights.

Step 2: List all possible Hamilton cycles.

Step 3: Find the weight of each cycle.

Step 4: Identify the Hamilton cycle of lowest weight.

Example 12.44

Applying the brute force method.

$A graph represents the five California air force bases. The graph has five vertices: E, B, V, L, and T. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. The edge, E T is labeled 370 miles. The edge, L T is labeled 396 miles. The edge, B T is labeled 84 miles. The edge, V T is labeled 396 miles.$

Step 2: List all the Hamilton cycles in the subgraph of the graph in Figure 12.222.

$A graph represents four cities. The graph has five vertices: E, B, V, L, and T. The edge, E B is labeled 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. The edge, E T is labeled 370 miles. The edge, L T is labeled 396 miles. The edge, B T is labeled 84 miles. The edge, V T is labeled 396 miles. The edges, E L, L V, L B, and L T are in dashed lines.$

To find the 6 cycles, focus on the three vertices in the middle, B, E, and V . The arrangements of these vertices are BEV, BVE, EBV, EVB, VBE , and VEB . These would correspond to the 6 cycles:

1: T → B → E → V → T

2: T → B → V → E → T

3: T → E → B → V → T

4: T → E → V → B → T

5: T → V → B → E → T

6: T → V → E → B → T

Step 3: Find the weight of each path. You can reduce your work by observing the cycles that are reverses of each other.

1: 84 + 410 + 207 + 396 = 1097 84 + 410 + 207 + 396 = 1097

2: 84 + 396 + 207 + 370 = 1071 84 + 396 + 207 + 370 = 1071

3: 370 + 410 + 396 + 396 = 1572 370 + 410 + 396 + 396 = 1572

4: Reverse of cycle 2, 1071

5: Reverse of cycle 3, 1572

6: Reverse of cycle 1, 1097

Step 4: Identify a Hamilton cycle of least weight.

Your Turn 12.44

Now suppose that the officer needed a cycle that visited all 5 of the Air Force bases in Figure 12.221. There would be ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 ( 5 − 1 ) ! = 4 ! = 4 × 3 × 2 × 1 = 24 different arrangements of vertices and ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 ( 5 − 1 ) ! 2 = 4 ! 2 = 24 2 = 12 distances to compare using the brute force method. If you consider 10 Air Force bases, there would be ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 ( 10 − 1 ) ! = 9 ! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362 , 880 different arrangements and ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 ( 10 − 1 ) ! 2 = 9 ! 2 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 2 = 181 , 440 distances to consider. There must be another way!

The Nearest Neighbor Method

$A graph represents the airfares between six different cities. The graph has 6 vertices. The vertices are A, B, C, D, E, and F. Edges from A leading to B, C, D, E, and F are labeled 250 dollars, 210 dollars, 300 dollars, 200 dollars, and 100 dollars. Edges from B leading to C, D, E, and F are labeled 220 dollars, 120 dollars, 160 dollars, and 170 dollars. Edges from C to D, E, and F are labeled 310 dollars, 180 dollars, and 330 dollars. Edges from D to E and F 270 dollars and 150 dollars. An edge from E to F is labeled 350 dollars.$

Mark F as V 2 Figure 12.225. The lowest of these is $150, which is the edge between F and D .

Mark D as V 3 Figure 12.226. The lowest of these is $120, which is the edge between D and B .

So, mark B as V 4 Figure 12.227. The lower amount is $160, which is the edge between B and E .

Now you can mark E as V 5 Figure 12.228. Make a note of the weight of the edge from E to C , which is $180, and from C back to A , which is $210.

Step 1: Select the starting vertex and label V 1 V 1 for "visited 1st." Identify the edge of lowest weight between V 1 V 1 and the remaining vertices.

Step 3: If vertices remain that have not been visited, repeat Step 2. Otherwise, a Hamilton cycle of low weight is V 1 → V 2 → ⋯ → V n → V 1 V 1 → V 2 → ⋯ → V n → V 1 .

Example 12.45

Using the nearest neighbor method.

Suppose that the candidate for governor wants to hold rallies around the state but time before the election is very limited. They would like to leave their home in city A , visit cities B , C , D , E , and F each once, and return home. The airfare between cities is not as important as the time of travel, which is indicated in Figure 12.229. Use the nearest neighbor method to find a route with relatively low travel time. What is the total travel time of the route that you found?

$A graph represents the airfares between six different cities. The graph has 6 vertices. The vertices are A, B, C, D, E, and F. Edges from A leading to B, C, D, E, and F are labeled 120 minutes, 140 minutes, 85 minutes, 90 minutes, and 180 minutes. Edges from B leading to C, D, E, and F are labeled 100 minutes, 80 minutes, 95 minutes, and 110 minutes. Edges from C to D, E, and F are labeled 220 minutes, 200 minutes, and 75 minutes. Edges from D to E and F are labeled 130 minutes and 70 minutes. An edge from E to F is labeled 210 minutes.$

Step 1: Label vertex A as V 1 V 1 . The edge of lowest weight between A and the remaining vertices is 85 min between A and D .

Step 2: Label vertex D as V 2 V 2 . The edge of lowest weight between D and the vertices that remain to be visited, B, C, E , and F , is 70 min between D and F .

Repeat Step 2: Label vertex F as V 3 V 3 . The edge of lowest weight between F and the vertices that remain to be visited, B, C, and E , is 75 min between F and C .

Repeat Step 2: Label vertex C as V 4 V 4 . The edge of lowest weight between C and the vertices that remain to be visited, B and E , is 100 min between C and B .

Repeat Step 2: Label vertex B as V 5 V 5 . The only vertex that remains to be visited is E . The weight of the edge between B and E is 95 min.

Your Turn 12.45

Check your understanding, section 12.9 exercises.

$Four graphs. Graph A has four vertices: a, b, c, and d. The edges are labeled as follows: a b, 3; b d, 3; d c, 1; c a, 2; a d, 1; b c, 2. Graph B has five vertices: e, f, g, h, and I. The edges are labeled as follows: e f, 2-thirds; f g, 5-twelfths; g h, 1-twelfth; h i, 3-fourths; i e, 1-fourth; e h, 1-half; e g, 1-sixth; f i, -third; f h, 5-sixths; g i, 1. Graph C has five vertices: i, j, k, m, and n. The curved edges are labeled as follows: k m, 20; m n, 30; n j, 40; j i, 50; i k, 10. The straight edges are labeled as follows: k j, 90; k n, 60; m i, 100; m j, 70; n i, 80. Graph d has four vertices; o, p, q, and r. The edges are labeled as follows: o p, 1.7; p q, 4.3; q r, 3.5; r o, 2.9 p r, 3.; o p, 1.2.$

IMAGES

Travelling salesman problem in c
Traveling Salesman Problem (TSP) with Miller-Tucker-Zemlin (MTZ) in
PPT
The Traveling Salesman Problem 14 different solutions
PPT
Travelling salesman problem in c

VIDEO

Travelling salesman problem
2.7 Travelling salesman problem
Travelling Salesman Problem -Explanation #shorts #shortsindia
Travelling Salesman Problem
Traveling Salesman Problem| NP- Class Problem
#15 Travelling salesman problem//DAA AKTU previous years question//@brevilearning

COMMENTS

Travelling salesman problem
The generalized travelling salesman problem, also known as the "travelling politician problem", deals with "states" that have (one or more) "cities", and the salesman must visit exactly one city from each state. One application is encountered in ordering a solution to the cutting stock problem in order to minimize knife changes.
Traveling Salesman Problem (TSP) Implementation
The Traveling Salesman Problem (TSP) is a classic algorithmic problem in the fields of computer science and operations research. It involves finding the shortest possible route that visits a set of cities and returns to the origin city. The challenge of TSP lies in its NP-hard nature, meaning that as the number of cities increases, the problem ...
Travelling Salesman Problem
The Travelling Salesman Problem (also known as the Travelling Salesperson Problem or TSP) is an NP-hard graph computational problem where the salesman must visit all cities (denoted using vertices in a graph) given in a set just once. The distances (denoted using edges in the graph) between all these cities are known.
Traveling salesman problem
The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1.
Traveling Salesperson Problem
Traveling Salesperson Problem. This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below. The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools.
DSA The Traveling Salesman Problem
The Traveling Salesman Problem states that you are a salesperson and you must visit a number of cities or towns. The Traveling Salesman Problem. Rules: Visit every city only once, then return back to the city you started in. Goal: Find the shortest possible route. Except for the Held-Karp algorithm (which is quite advanced and time consuming ...
Traveling Salesperson Problem
The traveling salesperson problem can be modeled as a graph. Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path ...
GraphicMaths
Travelling salesman problem. By Martin McBride, 2023-11-16. Tags: graph travelling salesman problem. Categories: graph theory computer science algorithm. The travelling salesman problem (often abbreviated to TSP) is a classic problem in graph theory. It has many applications, in many fields. It also has quite a few different solutions.
PDF The Traveling Salesman Problem
The traveling salesman problem is solved if there exists a shortest route that visits each destination once and permits the salesman to return home. (This route is called a Hamiltonian Cycle and will be explained in Chapter 2.) The traveling salesman problem can be divided into two types: the problems where there is a path between ...
Traveling Salesman Problem
The Traveling Salesman Problem, or TSP for short, is one of the most intensively studied problems in computational mathematics. These pages are devoted to the history, applications, and current research of this challenge of finding the shortest route visiting each member of a collection of locations and returning to your starting point.
Travelling Salesman Problem (Greedy Approach)
The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible ...
Traveling Salesman Problem: Exact Solutions vs. Heuristic vs
The Traveling Salesman Problem (TSP) is a well-known challenge in computer science, mathematical optimization, and operations research that aims to locate the most efficient route for visiting a group of cities and returning to the initial city.TSP is an extensively researched topic in the realm of combinatorial optimization.It has practical uses in various other optimization problems ...
12.9 Traveling Salesperson Problem
The traveling salesman problem involves finding the shortest route to travel between two points. True. False. 82. The traveling salesman problem can be represented as finding a Hamilton cycle of least weight on a weighted graph. True. False. 83.
How to Solve Traveling Salesman Problem
The traveling salesman problem is a classic problem in combinatorial optimization. This problem is finding the shortest path a salesman should take to traverse a list of cities and return to the origin city. The list of cities and the distance between each pair are provided. TSP is beneficial in various real-life applications such as planning ...
Traveling salesman problem
traveling salesman problem, an optimization problem in graph theory in which the nodes (cities) of a graph are connected by directed edges (routes), where the weight of an edge indicates the distance between two cities. The problem is to find a path that visits each city once, returns to the starting city, and minimizes the distance traveled.
Travelling Salesman Problem using Dynamic Programming
The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem. Naive Solution: 1) Consider city 1 as the starting and ending point. 2) Generate all (n-1)!
6.6: Hamiltonian Circuits and the Traveling Salesman Problem
This page titled 6.6: Hamiltonian Circuits and the Traveling Salesman Problem is shared under a CC BY-SA 3.0 license and was authored, remixed, and/or curated by David Lippman (The OpenTextBookStore) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is perhaps the most studied discrete optimization problem. Its popularity is due to the facts that TSP is easy to formulate, difficult to solve, and has a large number of applications. It appears that K. Menger was the first researcher to consider the Traveling Salesman Problem (TSP). He observed that the ...
Travelling Salesman Problem (Dynamic Approach)
Travelling Salesman Problem (Dynamic Approach) - Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.
Traveling Salesman Problem
The Travelling Salesman Problem (TSP) is a very well known problem in theoretical computer science and operations research. The standard version of TSP is a hard problem to solve and belongs to the NP-Hard class. In this tutorial, we'll discuss a dynamic approach for solving TSP. Furthermore, we'll also present the time complexity analysis ...
PDF The Traveling Salesman Problem
The Traveling Salesman Problem (TSP) is one of the most well-known combinatorial optimization problems. Its popularity and importance can be attributed to its simple deﬁnition but high complexity to solve it, making it an ideal research problem for design of new algorithms, development of complexity theory, and analysis of search ...
What is a Traveling Salesman Problem? Explained and Solved
The traveling salesman problem solutions offer various trade-offs between computational intricacies and the quality of the resolution, allowing practitioners to choose the best-suited approach based on their needs and problems. Here are the Top 5 solutions to the Traveling Salesman Problem (TSP): 1. Brute Force Algorithm
A faster heuristic for the Traveling Salesman Problem with Drone
28 May 2024 · Pedro H. D. B. Hokama , Carla N. Lintzmayer , Mário C. San Felice ·. Edit social preview. Given a set of customers, the Flying Sidekick Traveling Salesman Problem (FSTSP) consists of using one truck and one drone to perform deliveries to them. The drone is limited to delivering to one customer at a time, after which it returns ...
Learning collaborative policies to solve NP-hard routing problems
A. Croes. "A method for solving traveling salesman problems". In: Operations Research 5 (1958), pp. 791-812. Google Scholar Digital Library; Paulo R. de O. da Costa et al. Learning 2-opt Heuristics for the Traveling Salesman Problem via Deep Reinforcement Learning. 2020. arXiv: 2004.01608 [cs.LG]. Google Scholar; Gerhard Reinelt.
Exact solution approaches for the minimum total cost traveling salesman
Deployment of drones in delivery operations has been attracting growing interest from the commercial sector due to its prospective advantages for a range of distribution systems. Motivated by the widespread adoption of drones in last-mile delivery, we introduce the minimum cost traveling salesman problem with multiple drones, where a truck and multiple drones work in synchronization to deliver ...
12.10: Traveling Salesperson Problem
For the following exercises, use your solutions to the indicated exercises to compare the results of the brute force method to the results of the nearest neighbor method for each traveling salesman problem of finding a reasonably short route to leave from city U, visit each of the other cities listed and return to city U. Indicate whether the ...
European Journal of Operational Research
Edited by Alexander Hübner, Pedro Amorim, Jan Fransoo, Dorothee Honhon, Heinrich Kuhn, Victor Martínez de Albéniz, David Robb. 1 June 2021. View all issues. Read the latest articles of European Journal of Operational Research at ScienceDirect.com, Elsevier's leading platform of peer-reviewed scholarly literature.
Sustainability
The Traveling Salesman Problem with Drones (TSP-D) addresses scenarios where one vehicle and one or more drones are collaboratively optimized for operation. In contrast, the Vehicle Routing Problem with Drones (VRP-D) applies to cases involving multiple vehicles and multiple drones, all optimized together.

DAA Tutorial

Help Others, Please Share

Learn Latest Tutorials

Preparation

Trending Technologies

B.Tech / MCA

Traveling salesman problem

Description

Classifications of the TSP

Variations of the TSP

aTSP ILP Formulation

sTSP ILP Formulation

Exact algorithms

Heuristic algorithms

Tour construction procedures

Navigation menu

Traveling Salesperson Problem

Create the data

Other ways to create the distance matrix

Create the routing model

Create the distance callback

Set the cost of travel

Set search parameters

Add the solution printer

Solve and print the solution

Run the programs

Save routes to a list or array

Complete programs

Example: drilling a circuit board

Compute the distance matrix

Add the distance callback

Solution printer

Main function

Running the program

Changing the search strategy

Scaling the distance matrix

DSA Tutorial

Checking All Routes to Solve The Traveling Salesman Problem

Using A Greedy Algorithm to Solve The Traveling Salesman Problem

Other Algorithms That Find Near-Optimal Solutions to The Traveling Salesman Problem

Time Complexity for Solving The Traveling Salesman Problem

Actual Traveling Salesman Problems Are More Complex

COLOR PICKER

Contact Sales

Report Error

Top Tutorials

Traveling Salesperson Problem

Relationship to Graphs

The problem

Alternative applications and variants

Brute force algorithm

Nearest neighbour algorithm

Bellman–Held–Karp algorithm

Performance

Other algorithms

Join the GraphicMaths Newletter

Popular tags

Traveling Salesman Problem

12.9 Traveling Salesperson Problem

Brute Force and Greedy Algorithms

Example 12.42

Your Turn 12.42

Finding Weights of All Hamilton Cycles in Complete Graphs

Example 12.43

Your Turn 12.43

Example 12.44

Your Turn 12.44

The Nearest Neighbor Method

Example 12.45

Your Turn 12.45

Advanced Topics

Easy problems in Dynamic programming

Medium problems on Dynamic programming

Travelling Salesman Problem using Dynamic Programming

Hard problems on Dynamic programming

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Travelling Salesman Problem (Dynamic Approach)

The Traveling Salesman Problem